Method for solving three-dimensional coordinate conversion parameters based on random rotation angles
A three-dimensional coordinate, arbitrary rotation technology, applied in complex mathematical operations and other directions, can solve problems such as inability to accurately determine weights, different conversion parameters, and inability to give initial values
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
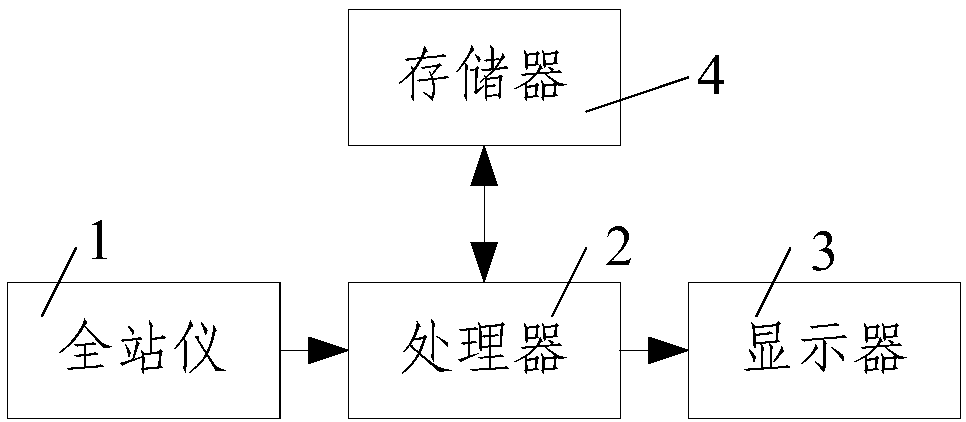
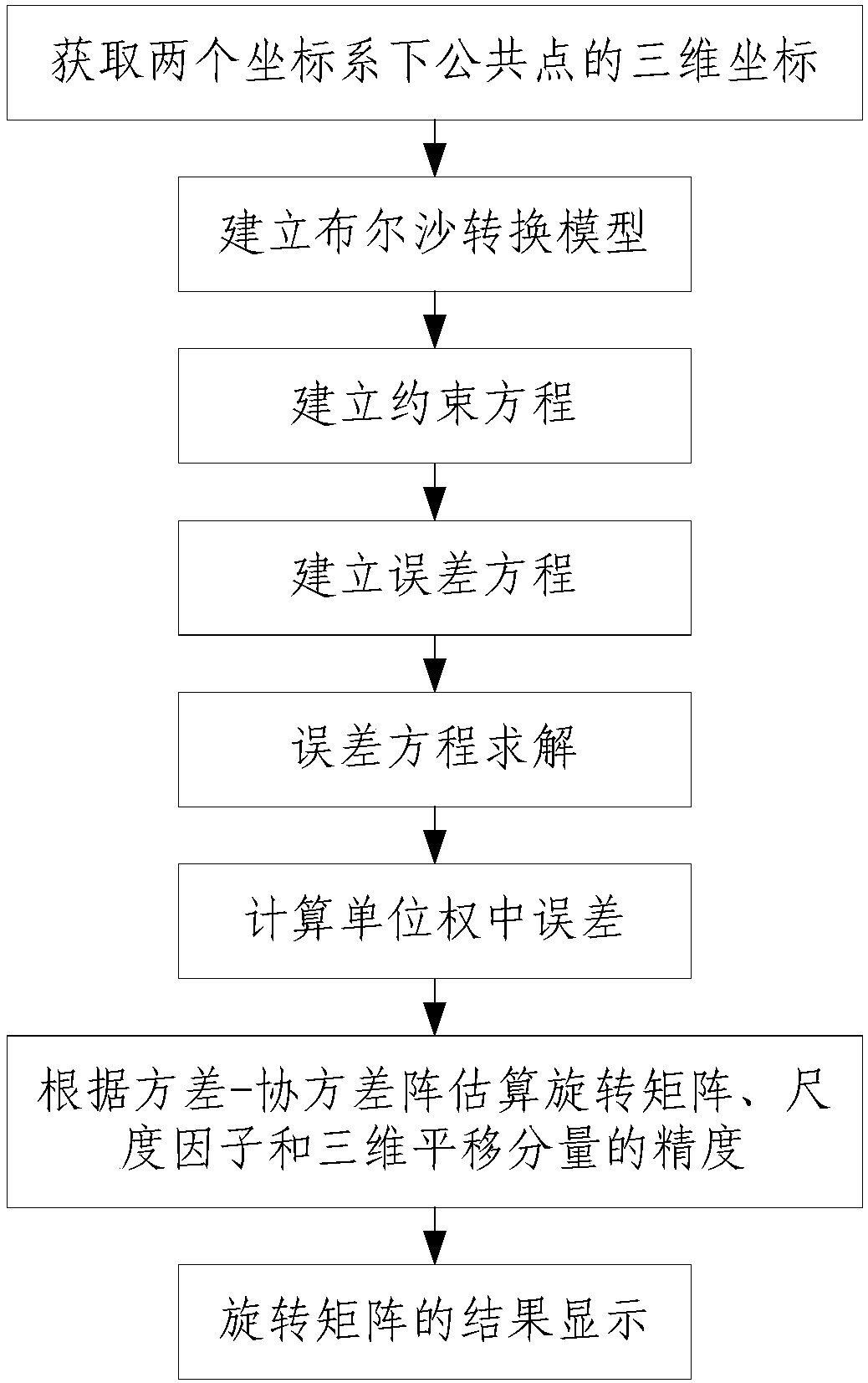
[0028] Such as figure 1 with figure 2 As shown, the present invention solves the method for any rotation angle three-dimensional coordinate transformation parameter, comprises the following steps:
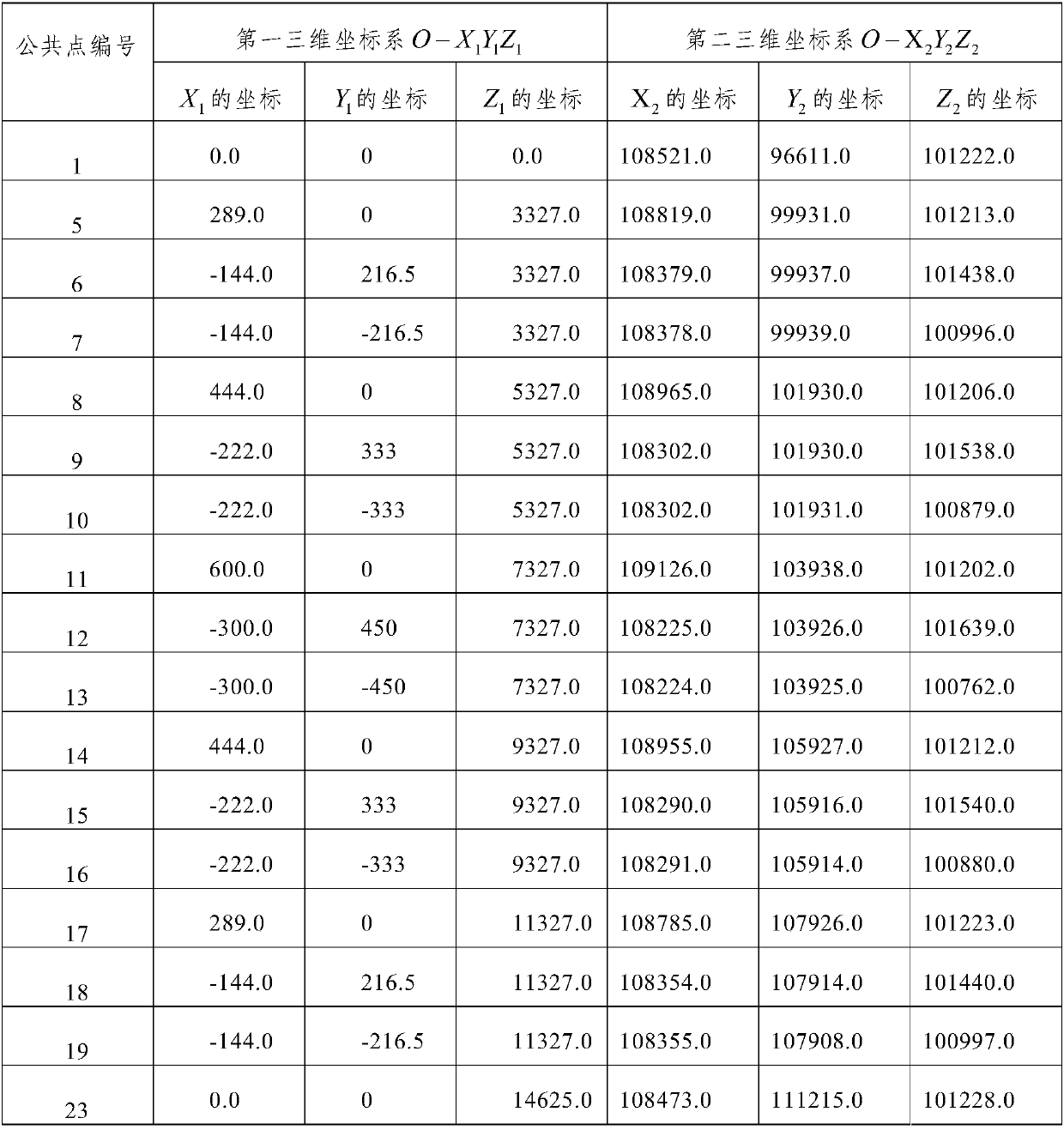
[0029] Step 1. Obtain the three-dimensional coordinates of the common points in the two coordinate systems: use the total station 1 to obtain multiple common points in the first three-dimensional coordinate system O-X 1 Y 1 Z 1 and the second three-dimensional coordinate system O-X 2 Y 2 Z 2 The three-dimensional coordinates in, and will get the first three-dimensional coordinate system O-X 1 Y 1 Z 1 The three-dimensional coordinates in and the second three-dimensional coordinate system O-X 2 Y 2 Z 2 The three-dimensional coordinates in are transmitted to the processor 2 connected with the total station 1;
[0030] In this embodiment, the first three-dimensional coordinate system O-X 1 Y 1 Z 1 and the second three-dimensional coordinate system O-X 2 Y 2 Z 2 It is...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com