Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Convex Nonnegative Matrix Factorization Method Based on Subspace Clustering

A non-negative matrix decomposition and subspace technology, which is applied to instruments, complex mathematical operations, calculations, etc., can solve problems such as subspace clustering and non-negative matrix decomposition collaborative optimization framework, etc., to improve the effect of image clustering, Robustness-enhancing effects

Active Publication Date: 2020-06-16
XI'AN INST OF OPTICS & FINE MECHANICS - CHINESE ACAD OF SCI
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The subspace reconstruction coefficients can be obtained by the subspace clustering method, however, the optimization process of the subspace clustering method is usually independent of the optimization process of the non-negative matrix factorization, and the cooperative optimization of subspace clustering and non-negative matrix factorization has not yet been seen. frame

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Convex Nonnegative Matrix Factorization Method Based on Subspace Clustering
  • Convex Nonnegative Matrix Factorization Method Based on Subspace Clustering
  • Convex Nonnegative Matrix Factorization Method Based on Subspace Clustering

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

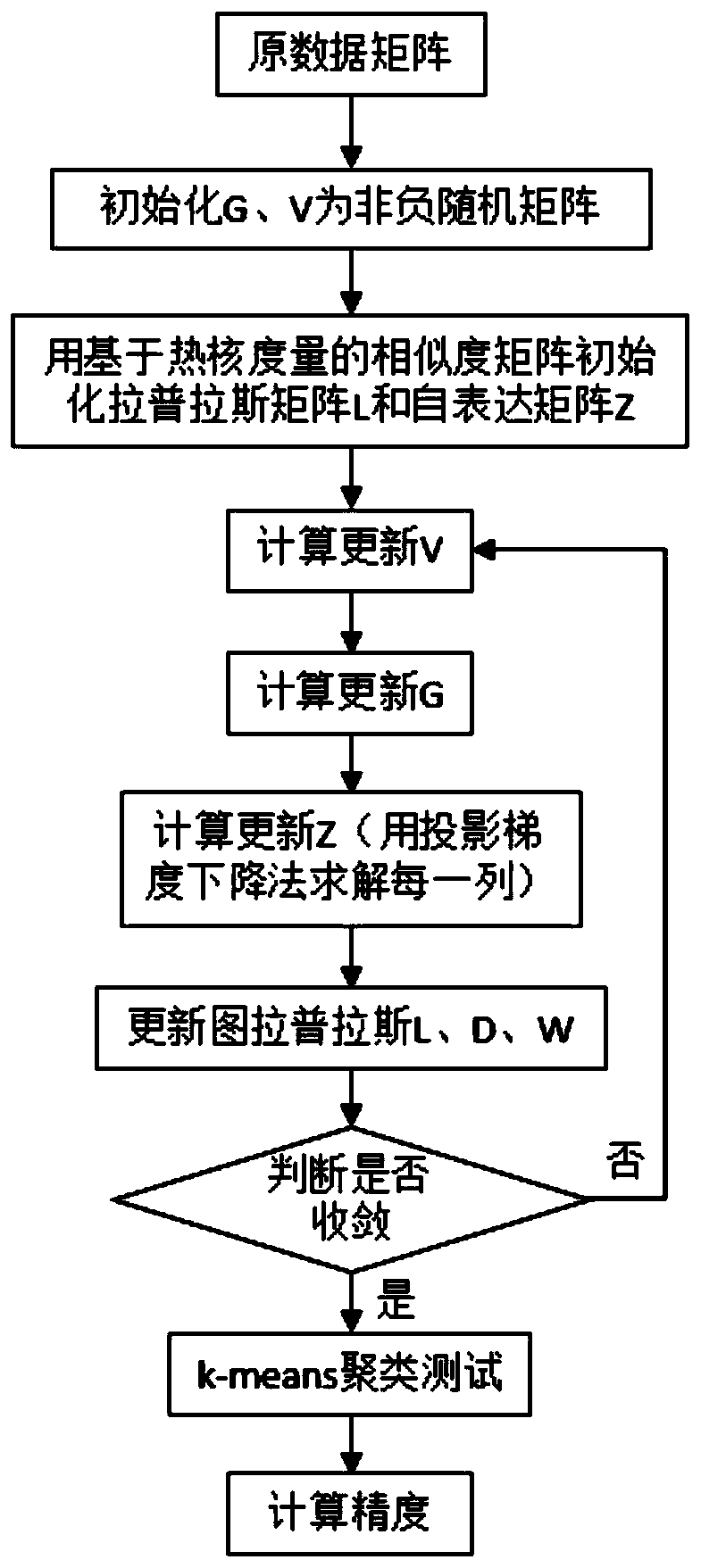
[0063] Embodiment one (with reference to figure 1 )

[0064] Step 1, decompose the original data matrix under the proposed subspace clustering-based convex non-negative matrix factorization framework.

[0065] (1a) Pull each image in the image sample set into a vector to form an m×n original data matrix X, m is the dimension of each sample, and n is the number of samples;

[0066] (1b) Initialize the matrix G of n×l 0 , l×n encoding matrix V 0 It is a non-negative random matrix, l=n s ×n c is the dimension of the learned low-dimensional non-negative subspace, n c is the total number of classes in the database, n s For the number of centers of each cluster, generally set n s =10, the number of iterations t=0.

[0067] (1c) Use the K nearest neighbor algorithm to construct the initial neighbor graph, the number of neighbors K is set to 5, and the initial graph Laplacian matrix L is calculated 0 , where L 0 =D 0 -W 0 , W 0 Represents a symmetric weight matrix, D 0 i...

Embodiment 2

[0095] Embodiment two (with reference to figure 2 )

[0096] Step 1, decompose the original data matrix under the proposed subspace clustering-based convex non-negative matrix factorization framework.

[0097] (1a) Pull each image in the image sample set into a vector to form an m×n original data matrix X, m is the dimension of each sample, and n is the number of samples;

[0098] (1b) Initialize the matrix G of n×l 0 , l×n encoding matrix V 0 It is a non-negative random matrix, l=n s ×n c is the dimension of the learned low-dimensional non-negative subspace, n c is the total number of classes in the database, n s For the number of centers of each cluster, generally set n s =10, the number of iterations t=0.

[0099] (1c) Use the K nearest neighbor algorithm to construct the initial neighbor graph, the number of neighbors K is set to 5, and the initial graph Laplacian matrix L is calculated 0 , where L 0 =D 0 -W 0 , W 0 Represents a symmetric weight matrix, D 0 is...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a convex non-negative matrix decomposition method based on subspace clustering. The realization steps are as follows: (1) pulling the images in the original database into vectors to form the original data matrix; The convex non-negative matrix decomposition of clustering is solved by two optimization methods to obtain the base matrix and encoding matrix; (3) clustering test of k-means clustering algorithm is performed on the encoding matrix, and the experimental results are counted to calculate the clustering accuracy and normalized mutual information two metrics. Compared with the existing method, the present invention excavates and utilizes the subspace structure information inside the data, and at the same time, the local subspace constraints imposed on the algorithm enhance the robustness of the algorithm and improve the image clustering effect; it can be widely used in data Mining, the field of data analysis.

Description

technical field [0001] The invention belongs to the technical field of information processing, and in particular relates to a non-negative low-dimensional data processing method, which can be used in data mining, data analysis and other fields. Background technique [0002] Non-negative matrix factorization as a feature extraction technique, since Lee and Seung's seminal work "Learning the Parts of Objects by Non-Negative Matrix Factorization, Nature, vol.401, no.6755, pp.788-791,1999" , the non-negative matrix factorization algorithm is becoming more and more popular in the field of computer vision and pattern recognition. In their work, it is pointed out that the non-negative constraints on the factor matrix can automatically learn the part-based representation of the data, which is closely related to the brain's perception mechanism. In addition to this discovery, another contribution of his work is to propose a simple but very effective solution algorithm. Thanks to th...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/16G06K9/62
CPCG06F17/16G06F18/23213
Inventor 李学龙崔国盛董永生
Owner XI'AN INST OF OPTICS & FINE MECHANICS - CHINESE ACAD OF SCI
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com