Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Thermal contact conduction modeling method for contact interface of channel and tapered roller

A technology of tapered rollers and contact interface, applied in the field of heat conduction, can solve the problems such as the influence of contact parameters

Pending Publication Date: 2022-04-12
CHONGQING UNIV
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

So far, fractal contact mechanics models have not been implemented directly for tapered roller / ditch interfaces because surface geometry and contact form have an influence on contact parameters
In addition, there is no relevant research on the TCC modeling of the tapered roller / channel interface, but the TCC modeling of the tapered roller / channel interface is important for the engineering thermal analysis of tapered roller bearings and machine tools

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Thermal contact conduction modeling method for contact interface of channel and tapered roller
  • Thermal contact conduction modeling method for contact interface of channel and tapered roller
  • Thermal contact conduction modeling method for contact interface of channel and tapered roller

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0104] The present invention will be further described below in conjunction with the accompanying drawings and specific embodiments, so that those skilled in the art can better understand the present invention and implement it, but the examples given are not intended to limit the present invention.

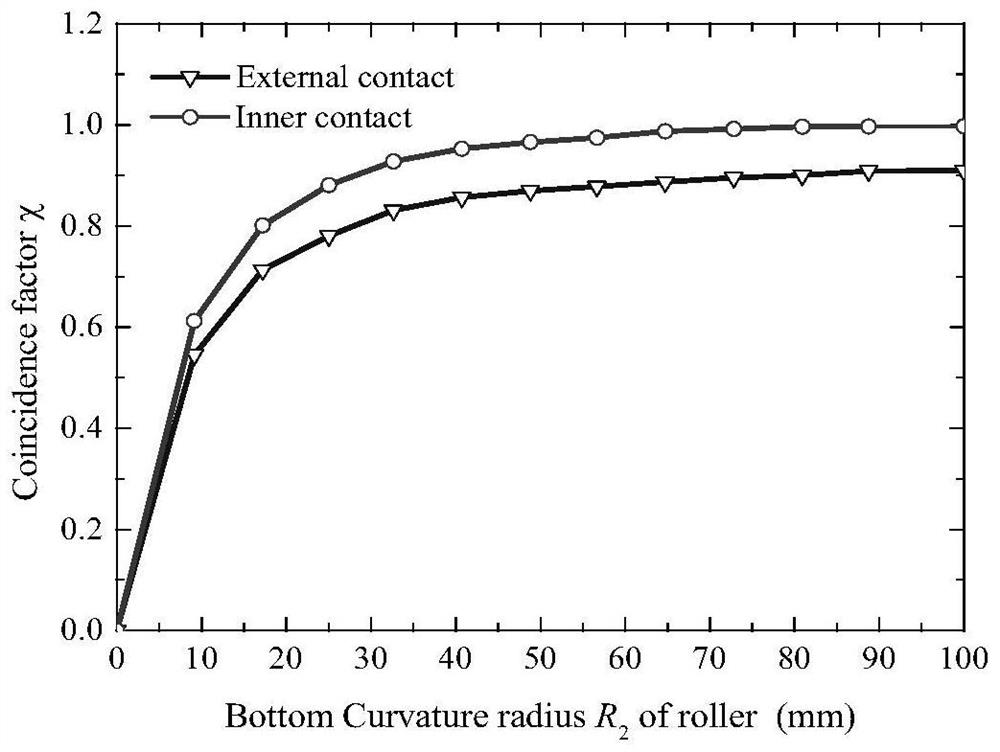
[0105] The thermal contact conduction modeling method of the channel and the tapered roller contact interface in this embodiment includes the following contents:

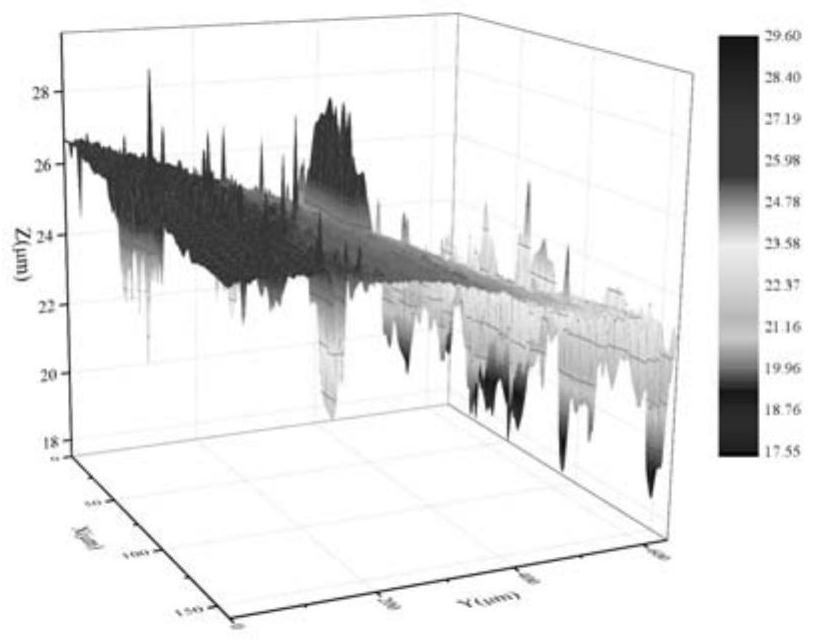
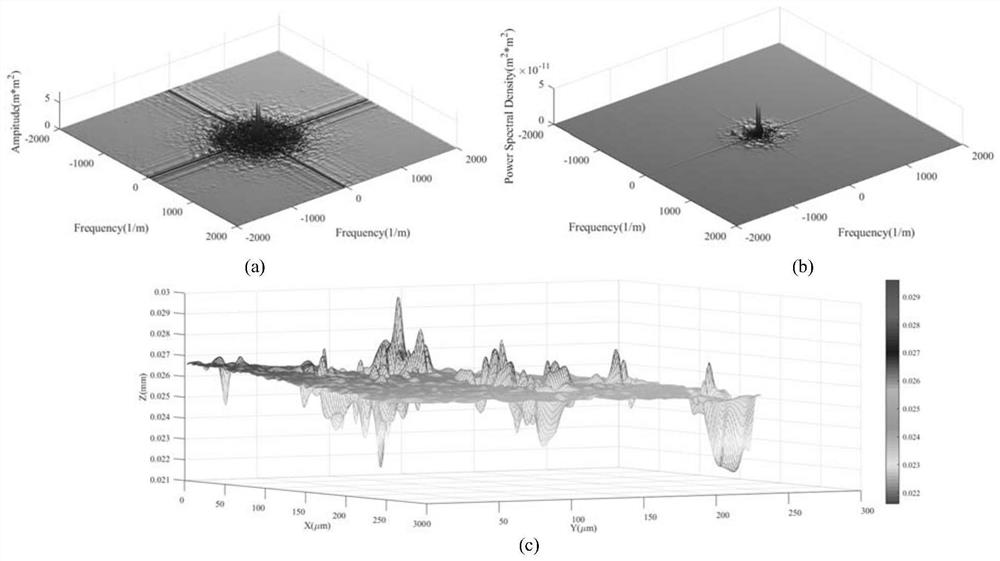
[0106] 1. Characterize the surface morphology

[0107] Generate rough surfaces using fractal theory and Monte Carlo methods to obtain fractal dimensions.

[0108] Further, the Weierstrass-Mandelbrot fractal surface with fractal dimension D is expressed as:

[0109]

[0110] Among them, C n is an independent and obeys normal distribution N(μ=0,σ 2 =1) true random number; A n and B n It is an independent and uniformly distributed true random number on [0,2π]; 2

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a thermal contact conduction modeling method for a contact interface of a channel and a tapered roller, which comprises the following steps of: representing surface topography: generating a rough surface by using a fractal theory and a Monte Carlo method to obtain fractal dimensions; constructing a contact model: introducing a coincidence factor aiming at the geometrical shape and the contact form of the tapered roller / channel interface, and correcting the contact area and the contact load by utilizing the coincidence factor; and constructing a thermal contact conduction model: constructing the thermal contact conduction model based on the surface topography characterization and the contact model by combining matrix thermal contact conduction and shrinkage heat basic conduction. According to the thermal contact conduction modeling method for the contact interface of the channel and the tapered roller, the analysis requirement of thermal contact conduction of the tapered roller / channel interface can be met.

Description

technical field [0001] The invention belongs to the technical field of heat conduction, in particular to a thermal contact conduction modeling method at the contact interface between a channel and a tapered roller. Background technique [0002] The modeling and experimental study of thermal contact conduction (TCC) has received a lot of attention because it is crucial for engineering thermal analysis. For example, introducing TCC in the thermal analysis of machine tool can show that TCC determines the temperature field of the whole machine tool. In fact, TCC is related to surface topography, contact load, material properties, actual contact area, etc. The mapping between TCC and the above parameters is nonlinear, and TCC modeling is an interdisciplinary problem involving geometry, contact mechanics, and heat. The surface topography mainly determines the contact area. Bearings are important functional components in precision machine tools and are obvious heating elements. ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/17G06F30/20G06F17/18G06F111/08G06F119/08
Inventor 马驰刘佳兰桂洪泉李梦媛王时龙
Owner CHONGQING UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com