Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Image stitching method and device

An image stitching and field of view technology, applied in image analysis, image data processing, instruments, etc., can solve the problems of inaccurate reference field of view and low image quality, and achieve the effect of small cumulative deformation and improved image quality.

Inactive Publication Date: 2014-07-23
TCL CORPORATION
View PDF3 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The embodiment of the present invention provides an image stitching method, which aims to solve the problem that the existing method selects the reference field of view inaccurately, which leads to the problem that the quality of the stitched image is too low

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Image stitching method and device
  • Image stitching method and device
  • Image stitching method and device

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

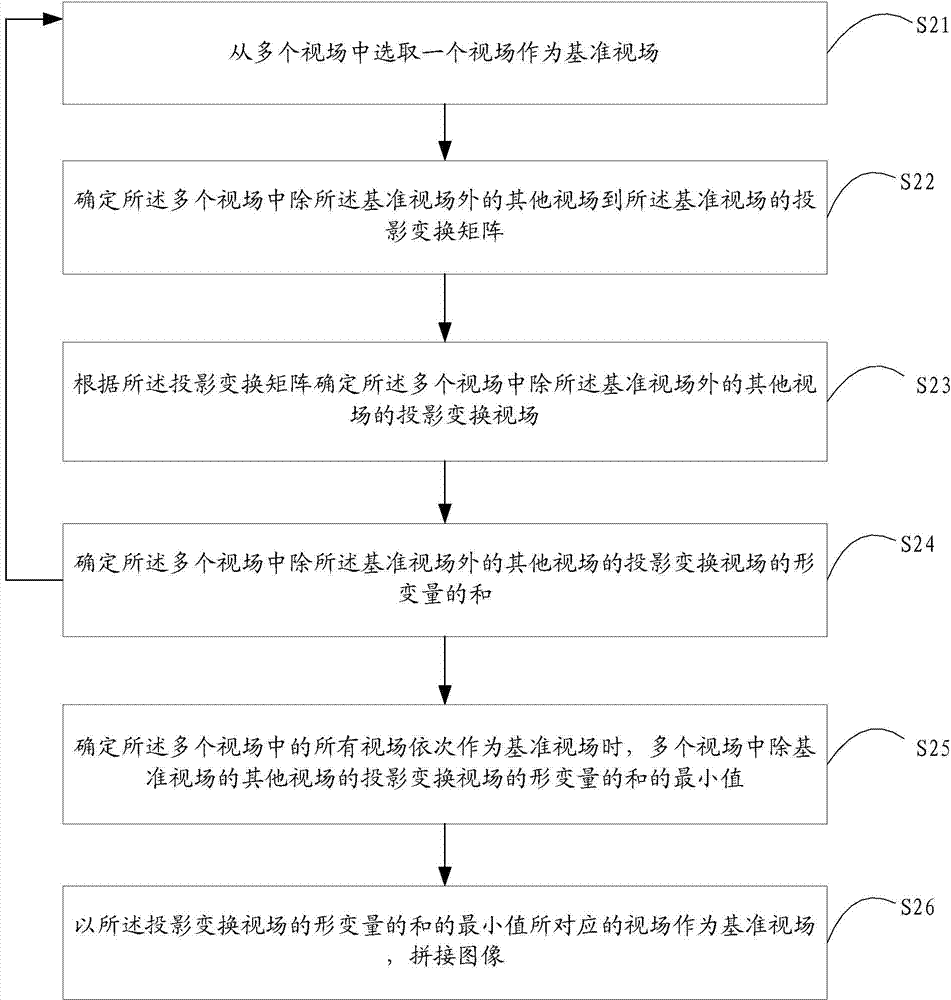
[0035] figure 2 A flow chart of an image mosaic method provided by the first embodiment of the present invention is shown, and the details are as follows:

[0036] Step S21, selecting a field of view from the plurality of fields of view as a reference field of view.

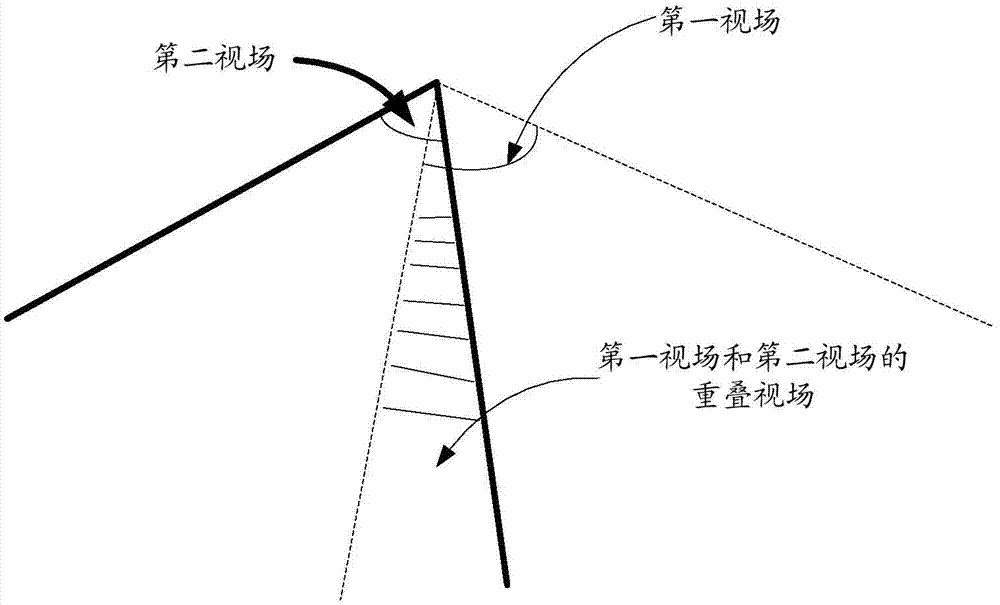
[0037] In this step, multiple cameras shoot multiple fields of view from different angles, and any two adjacent fields of view have a certain overlapping area, so that the fields of view captured by any two cameras can transition through the overlapping area. Randomly select one field of view from the multiple fields of view captured as the reference field of view.

[0038] Step S22 , determining projection transformation matrices from other viewing fields in the multiple viewing fields except the reference viewing field to the reference viewing field.

[0039] In this step, when a reference field of view is selected, other fields of view are projected and transformed into the reference coordinate system where...

Embodiment 2

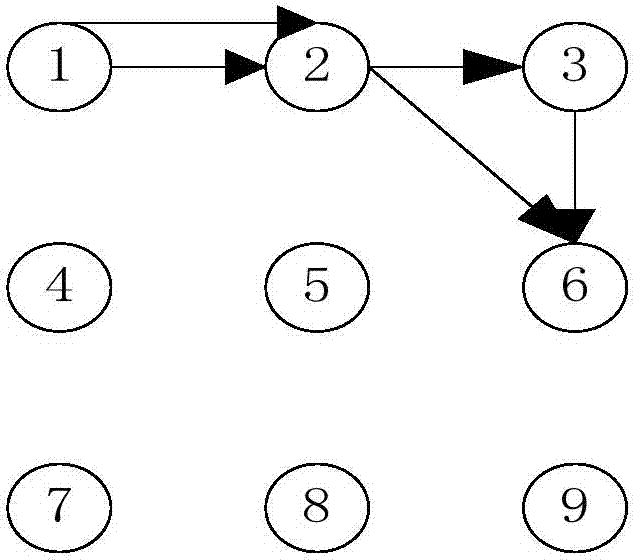
[0090] The following specifically introduces how to determine the shortest path from the field of view projected to the reference field of view. In this embodiment, each field of view is abstracted as a node, which is described in detail as follows:

[0091] First create three tables, namely HIGHER table, TEMP table and LOWER table. The HIGHER table saves the determined nodes and is initially empty; the LOWER table saves undetermined nodes and initially contains all m nodes; the TEMP table is a temporary table. Initially empty.

[0092] The algorithm flow is:

[0093] Step 1: Assuming that the node Vs is selected as the source node, remove it from the LOWER table and put it into the HIGHER table;

[0094] Step 2: Traverse each node in the HIGHER table, for any node V i ∈ HIGHER table, in the LOWER table find the node V i All adjacent nodes, first calculate the relationship between these nodes and V i The projection transformation matrix between, on this basis, calculate th...

Embodiment 3

[0104] Figure 9 A structural diagram of an image stitching device provided by the third embodiment of the present invention is shown, and for convenience of description, only parts related to the embodiment of the present invention are shown. The image stitching device corresponds to the image stitching method of the above-mentioned embodiment.

[0105] In this embodiment, the image stitching device includes: field of view selection unit 91, projection transformation matrix determination unit 92, projection transformation field of view determination unit 93, first deformation amount determination unit 94, second deformation amount determination unit 95, image stitching Unit 96. in:

[0106] The field of view selection unit 91 is configured to select one field of view from a plurality of fields of view as a reference field of view.

[0107] A projection transformation matrix determining unit 92, configured to determine projection transformation matrices from other fields of...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the field of image stitching and provides an image stitching method and device. The image stitching method comprises the steps that one of multiple view fields is selected as a datum view field; a projection transformation matrix from the multiple view fields except the datum view field to the datum view field is determined; according to the projection transformation matrix, projection transformation view fields of the multiple view fields except the datum view field are determined; the sum of deformation quantities of the projection transformation view fields of the multiple view fields except the datum view field is determined; when all the view fields are used as the datum view field in sequence, the minimum of the sum of the deformation quantities of the projection transformation view fields of the multiple view fields except the datum view field is determined; the view field corresponding to the minimum of the sum of the deformation quantities of the projection transformation view fields is used as the datum view field, and then image stitching is conducted. By the adoption of the image stitching method and device, the image stitching quality can be improved.

Description

technical field [0001] The invention belongs to the field of image splicing, and in particular relates to an image splicing method and device. Background technique [0002] Panoramic stitching technology refers to a group of images or video sequences with overlapping areas, according to a certain mapping relationship, through spatial registration, to associate pixels in different coordinate systems, so as to combine the same viewpoint or multiple different viewpoints. The video sequences are stitched into a new image with a wide viewing angle, a large range, and a natural transition that contains the information of each image. The key and core of panoramic stitching technology is to accurately find the position and range of overlapping areas of adjacent images, and to combine video sequences with overlapping fields of view (that is, overlapping areas) into a panoramic image requires the establishment of a unified coordinate transformation relationship. Among them, the schem...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06T7/00
Inventor 张艳
Owner TCL CORPORATION
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com