Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Optimal integral sliding mode control method

A control method and integral sliding mode technology, applied in the field of control, can solve problems such as the inability to effectively compromise the system response time and overshoot, and the inability to achieve finite time convergence of the system state.

Inactive Publication Date: 2015-09-30
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF4 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The conventional infinite-time state-dependent Riccati equation (SDRE) control method can only guarantee the gradual convergence of the system state, but cannot achieve the finite-time convergence of the system state; at the same time, it cannot effectively compromise the contradiction between the system response time and the overshoot

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimal integral sliding mode control method
  • Optimal integral sliding mode control method
  • Optimal integral sliding mode control method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

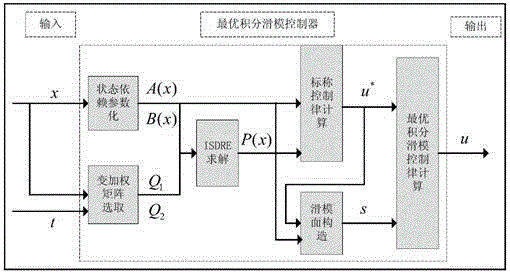
[0083] This embodiment is aimed at the description of the nominal system without disturbance, and mainly explains the advantages of the improved control method based on the state-dependent Riccati equation (ISDRE). An optimal integral sliding mode control method disclosed in this embodiment includes the following steps :

[0084] Step 1, establish a dynamic model of the second-order nonlinear system. The dynamic model of the second-order nonlinear system is shown in formula (1).

[0085] System initial value x 0 =[-4,2] T . f(x)=0.3sin(x 1 +2x 2 )-2x 1 +x 2 , g(x)=0.5sin(x 1 +x 2 )+1.

[0086] Extending the linearization of this nonlinear system, the form of the state correlation coefficient SDC (state-dependent coefficient) is obtained as shown in formula (2), where the parameter matrix is ​​constructed in the following form:

[0087] A ( x ) = 0 ...

Embodiment 2

[0102] This embodiment is due to the advantages of the improved optimal sliding mode control method based on the state-dependent Riccati equation (ISDRE) proposed by the present invention, such as Figure 7 As shown, an optimal integral sliding mode control method disclosed in this embodiment includes the following steps:

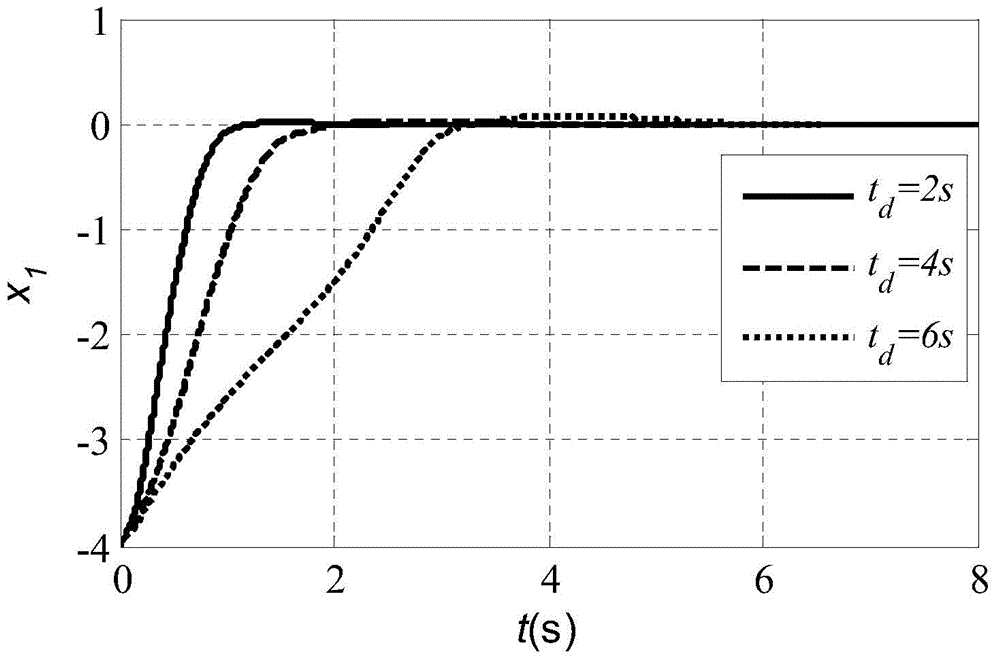
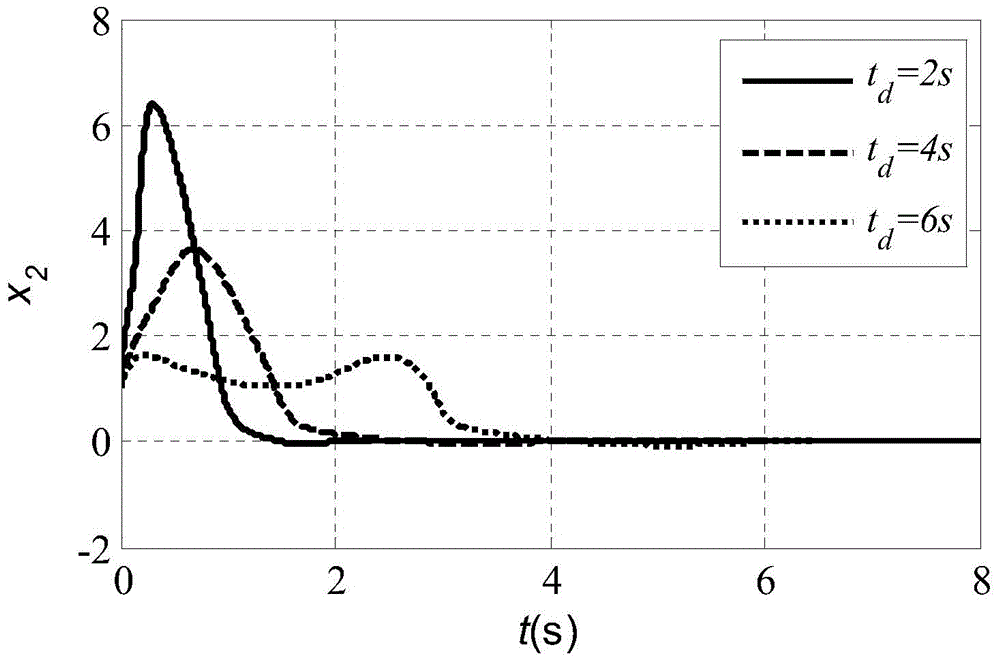
[0103] Step 1, establish the dynamic model of the second-order nonlinear system with disturbance. The dynamic model of the second-order nonlinear system is shown in formula (9). Wherein the system parameters are the same as in Embodiment 1, and the disturbance term d(x, t)=0.6sin(10t)+0.2cos(0.5x 1 +7x 2 ). The disturbance term d(x,t) satisfies the matching condition and is bounded, and the upper bound of |d(x,t)| has a maximum value △d max = 0.8.

[0104] Step 2. For the nominal system without the disturbance term d(x,t), a control law based on the improved state-dependent Riccati equation (ISDRE) is given. The steps and forms for solving the control...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an optimal integral sliding mode control method, relates to an integral sliding mode control method, and belongs to the technical field of control. The optimal integral sliding mode control method includes the steps: firstly, building a dynamic model of a second-order nonlinear system; secondly, realizing system state finite-time convergence through an ISDRE (improved state-dependent Riccati equation), and effectively compromising the contradiction between system response time and overshoot; thirdly, combining the ISDRE with an integral sliding mode to further improve robustness of the system under disturbance. The optimal integral sliding mode control method has universality, and can be applied to control systems such as an aircraft and an inverted pendulum.

Description

technical field [0001] The invention relates to an integral sliding mode control method, in particular to an optimal integral sliding mode control method, and belongs to the technical field of control. Background technique [0002] As an important branch of modern control theory, optimal control has achieved great development. The control method uses the optimization strategy to obtain the control quantity that meets the specific performance index, and can obtain the expected system dynamics, which effectively improves the response characteristics of the system. For linear systems, research on optimal control algorithms based on quadratic performance indicators has been fully developed, and rich theoretical basis and design experience have been accumulated. However, for nonlinear systems, due to the complexity of the system form, for the general quadratic performance index optimization problem, it is impossible to obtain the optimal problem analytical solution through algeb...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05B13/04
Inventor 盛永智巩轶男刘向东
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com