Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Calculation Method of Negative Bending Moment Impact Coefficient of Medium and Small Span Continuous Girder Bridge

A technology of impact coefficient and small and medium spans, applied in calculation, electrical digital data processing, special data processing applications, etc., can solve the problem of providing reliable data statistics support for negative bending moment impact coefficients of fulcrum sections of continuous girder bridges, etc.

Active Publication Date: 2018-10-12
CHANGAN UNIV +1
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The vibration forms of the negative moment section and the positive moment section of the continuous girder bridge are different, and the dynamic impact mechanism of the vehicle load on them is different. Supported by statistical data, at the same time, it is known from formula (1) that the impact coefficient u is related to the influence line of internal force

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Calculation Method of Negative Bending Moment Impact Coefficient of Medium and Small Span Continuous Girder Bridge
  • A Calculation Method of Negative Bending Moment Impact Coefficient of Medium and Small Span Continuous Girder Bridge
  • A Calculation Method of Negative Bending Moment Impact Coefficient of Medium and Small Span Continuous Girder Bridge

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

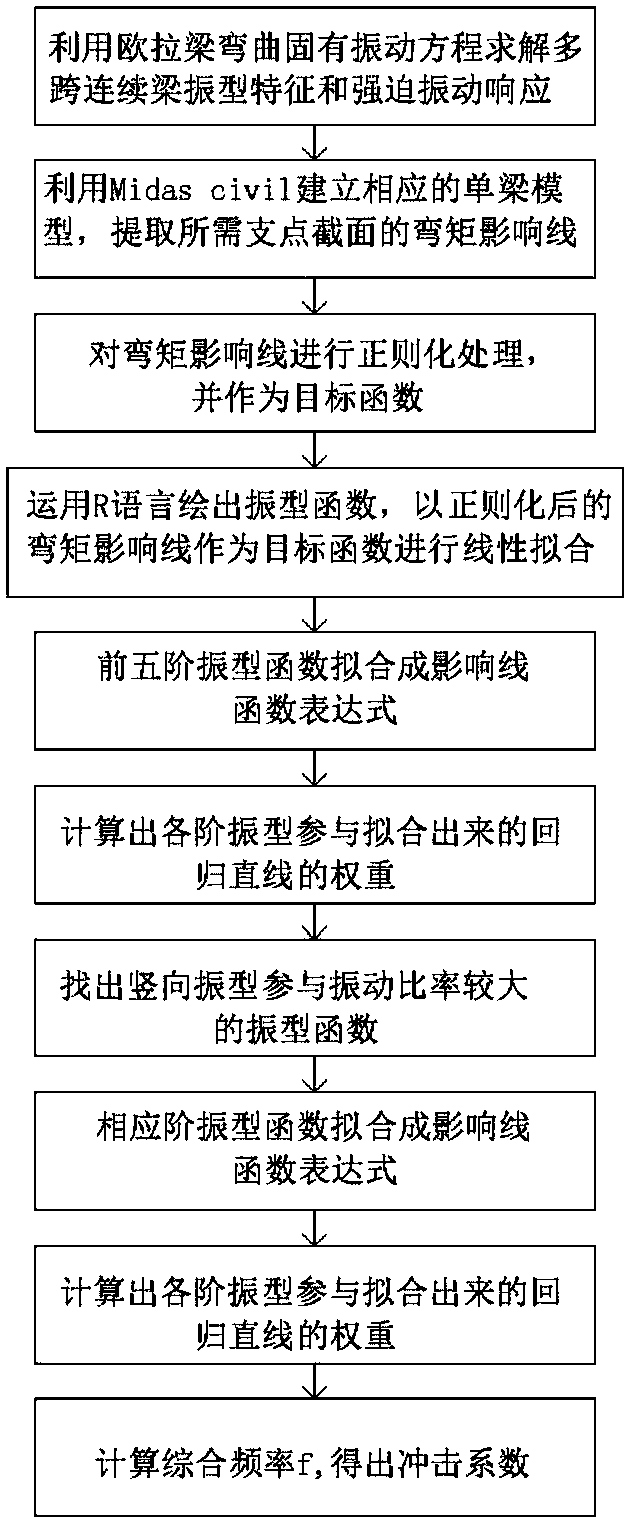
[0084] Embodiment 1: Taking continuous beams with three spans and equal spans and equal sections as an example, see figure 1 , the inventive method comprises the following steps:

[0085] Step 1: Using the natural vibration equation of Euler beam bending

[0086]

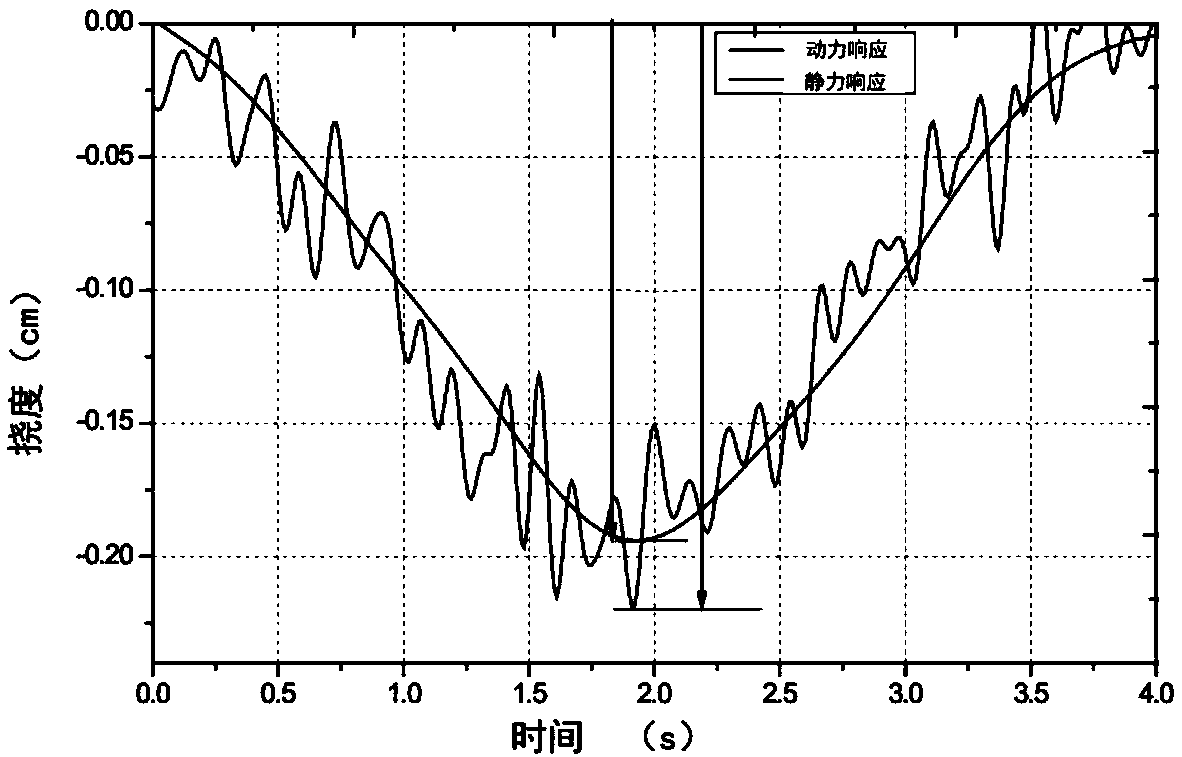
[0087] In the formula: y-the dynamic deflection y(x,t) of the beam from the static balance position meter, which is positive downward; x-the horizontal distance from the end of the beam; t-time effect; P(t)-transverse load ;

[0088] Solve the mode shape eigenvalues ​​and forced vibration responses of multi-span continuous beams, and obtain the nth order vibration mode formula of the sth span, as follows:

[0089] Y ns (x)=A ns sina ns x+B ns cosa ns x+C ns sinha ns x+D ns cosha ns x

[0090]

[0091] In the formula: A ns , B ns 、C ns 、D ns - undetermined coefficient;

[0092] The first and second derivatives are:

[0093] Y' ns (x)=a ns (A ns cosa ns x-B ns sina ns x+C ns cosha ns x...

Embodiment 2

[0124] Embodiment two: take two-span continuous beams as the utilization mode superposition method of the present invention to find the impact coefficient:

[0125] Step 1: see Figure 15 , substituting the boundary conditions of the 2*30m two-span continuous girder bridge into formulas (7) to (9), the undetermined coefficient A can be obtained ns , B ns 、C ns 、D ns The value of and its natural frequency are shown in formula (10):

[0126]

[0127] Where: ω n —Nth order natural vibration frequency

[0128] Step 2: Use Midas Civil software to establish a 2×30m small box girder single-girder model, and analyze the bending moment influence line mode of the fulcrum 2 section. See the results Figure 17 , regularize the bending moment influence line, and use the regularized influence line function ( Figure 18 ) as the objective function;

[0129] Step 3: Normalize the mode shape values ​​of the two-span continuous beam obtained in step 1, and then use the R language pro...

Embodiment 3

[0145] Embodiment three: take the four-span continuous beam as the utilization mode shape superposition method of the present invention to find the impact coefficient:

[0146] Step 1: 4*30m four-span continuous girder bridge (see Figure 24 ) into the formula (7) ~ formula (9), the undetermined coefficient A can be obtained ns , B ns 、C ns 、D ns The value of and its natural frequency are shown in formula (10):

[0147]

[0148] Where: ω n - the nth order natural vibration frequency;

[0149] Step 2: Use Midas Civil software to establish a 4×30m small box girder single girder model, and analyze the bending moment influence line mode of the fulcrum 2 section, see the results Figure 26 , regularize the bending moment influence line, and use the regularized influence line function ( Figure 27 ) as the objective function;

[0150] Step 3: Normalize the mode shape values ​​of the four-span continuous beam obtained in Step 1, and then take the bridge length (L) as the a...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a calculation method of a small and medium-span continuous bridge hogging moment impact coefficient. A small and medium-span continuous bridge is taken as an object, the characteristics, including the structural style, the geometrical morphology, the supporting situation, the quality, the rigidity and the like, of the bridge as well as the influence factors of the impact coefficients, including the amount, the axle number, the axle weight, the axle interval, the driving speed and the like of a vehicle are comprehensively considered, a method of combining theoretical analysis with numerical simulation is adopted to solve a computational formula problem of the regression fitting of the continuous bridge hogging moment impact coefficient according to an interrelation between the impact coefficient and an internal force influence line, the vehicle-mounted dynamic behaviors and mechanisms of the continuous bridge are disclosed, a bridge design theory and a bridge calculation method can be enriched, references are provided for bridge dynamics assessment, and the calculation method is accelerated to be widely applied and developed.

Description

technical field [0001] The invention belongs to the technical field of traffic bridges, and in particular relates to a calculation method for the negative moment impact coefficient of a continuous girder bridge with a medium and small span. Background technique [0002] The detection of bridge impact coefficient has extremely far-reaching significance for bridge design, maintenance and reinforcement. If the impact coefficient of bridge structure cannot be accurately detected, it will lead to unreasonable design of new bridges or untimely maintenance and reinforcement of old bridges, which will cause bridge damage caused by vehicle loads. In severe cases, major accidents will occur, causing loss of people's lives and property. [0003] The bridge under the action of dynamic load produces dynamic effects in the horizontal, vertical and vertical directions of space, and the vertical dynamic effect is called the impact effect. Usually, the total vertical load effect of moving l...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/50
CPCG06F30/367
Inventor 周勇军石雄伟袁卓亚赵煜王业路徐婷婷
Owner CHANGAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com