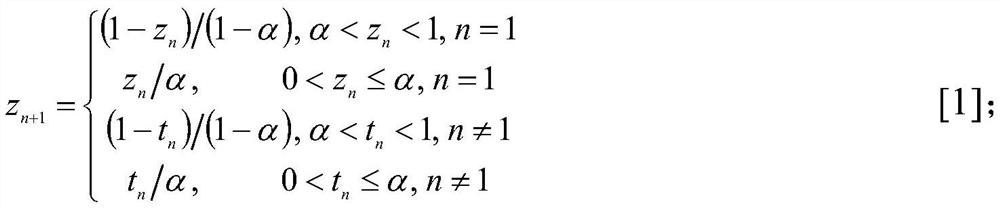A Chaotic Spread Spectrum Sequence Generation Method Based on Dynamic Multi-map Recombination

A technology of spread spectrum sequence and generation method, which is applied in the field of chaotic spread spectrum sequence generation based on dynamic multi-mapping compounding, and can solve problems such as the performance impact of chaotic sequences

Active Publication Date: 2022-05-20

SHENYANG LIGONG UNIV

2 Cites 0 Cited by

AI-Extracted Technical Summary

Problems solved by technology

However, as the system spread spectrum address code is a finite length sequence, the performance of the infinitely long chaotic sequence ...

Abstract

The generation method of chaotic spread spectrum sequence based on dynamic multi-mapping composite, to cope with the limitation of the limited number of sequences and the fixed mechanism of chaotic communication, this method is proposed based on the research basis of the improved Logistic, Chebyshev, and Kent three mappings. Use the control parameters to select the odd map and the even map from the improved Logistic, Chebyshev, and use the Kent map to establish a fractal function, thereby driving the fractal parameters of the odd map and the even map, and then the output of the odd map drives the initial value of the even map, and the even map The output of drives the initial value of the odd map. The selection function is established through the association of the odd map and the even map, and drives the initial value of the Kent map. Thus, the final new sequence is output through the optimization function of odd and even maps. This method can provide more address codes for the spread spectrum communication system, thereby expanding the application of the communication system.

Application Domain

Securing communication by chaotic signalsHigh level techniques

Technology Topic

Computational physicsControl parameters +5

Image

Examples

Experimental program(1)

Example Embodiment

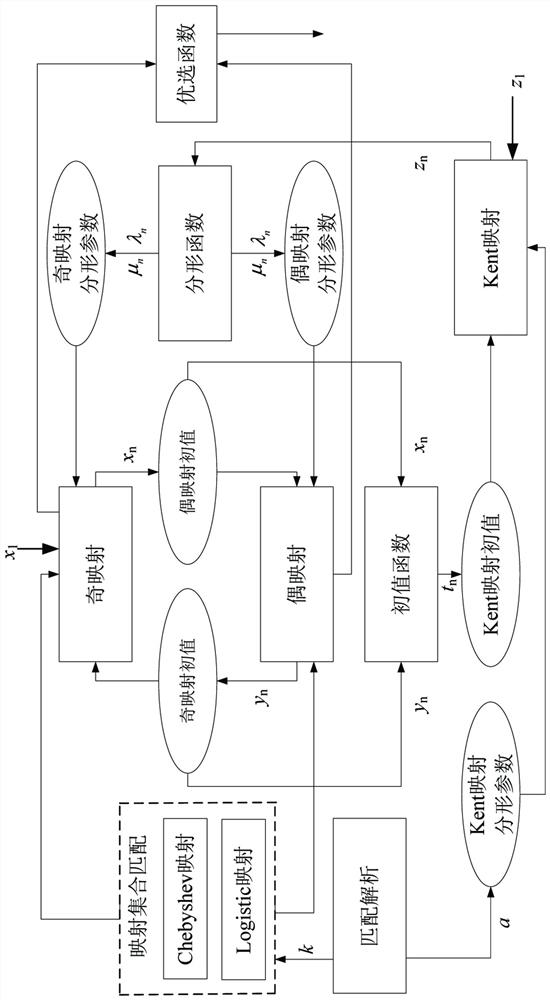
[0010] 1) Pass input parameters, namely: control parameter k, initial value parameter z 1 and x 1 , the fractal parameter α. Among them, the initial value parameter z 1 The value range is (0,1), the initial value parameter x 1 The value range is (-1,1). The value range of the fractal parameter α is (0,1). The control parameter k is set to 0 or 1, mainly controlling the matching of odd and even mappings from the set of Chebyshev mapping and improved Logistic mapping. When k=0, Chebyshev mapping is odd mapping, and improved Logistic mapping is even mapping. When k=1, the improved Logistic mapping is an odd mapping, and the Chebyshev mapping is an even mapping.

[0011] 2) According to the analysis of the input parameters, the fractal parameter α of the Kent map is obtained. Since the Kent map shows the best chaotic shape when α=0.4997, the trigger fractal parameter α when the system is started is set to 0.4997. (that is, when n=1), the initial value z of the Kent mapping 1 Entered by the user, the initial value of the Kent map after startup is set by t n Based on this, formula (1) is used to iteratively generate the Kent sequence.

[0012]

[0013] where, t n is the output of the initial value function of formula (7), and the value range is (0, 1).

[0014] 3) Then, use the generated Kent sequence value z of the current rank n n Carry out the fractal function calculation of formula (2) to obtain the fractal parameter λ of the Chebyshev map n and the fractal parameter μ of the improved logistic map n.

[0015]

[0016] Fractal parameter λ n can satisfy λ n ≥4, so that the Chebyshev mapping reaches full mapping. Fractal parameter μ n The value range is [1.4, 2], which makes the improved Logistic mapping reach full mapping.

[0017] 4) Perform the odd mapping iterative operation, the initial value x of the odd mapping when the system starts (that is, when n=1) 1 Input by the user, after startup, the initial value of odd mapping is determined by the sequence of even mapping y n drive. When the control parameter k=0, use the initial value of odd mapping and fractal parameter λ n , perform the odd mapping iteration of formula (3) to generate a Chebyshev sequence, and the initial value of the Chebyshev sequence ranges from [-1, 1]. When the control parameter k=1, the initial value of odd mapping and the fractal parameter μ are used n , perform the odd mapping iteration of formula (4) to generate an improved Logistic sequence, and the range of the initial value of the improved Logistic sequence is also [-1, 1].

[0018]

[0019]

[0020] 5) Perform even mapping iterative operation, and the initial value of even mapping is determined by the odd mapping sequence x n drive. When the control parameter k=0, the initial value of the even map and the fractal parameter μ are used n , perform the even mapping iteration as shown in formula (5) to generate an improved Logistic sequence, and the initial value of the improved Logistic sequence ranges from [-1, 1]. When the control parameter k=1, the initial value of the even map and the fractal parameter λ are used n , perform the even mapping iteration as shown in formula (6) to generate a Chebyshev sequence, and the value range of the initial value of the Chebyshev sequence is also [-1, 1].

[0021] y n+1 =1-μ n x n 2 ,-1≤x n ≤1 (5).

[0022] y n+1 =cos(λ n cos -1 x n ),-1≤x n ≤1 (6).

[0023] 6) Use odd mapping sequence x n Sum-even mapping sequence y n Perform initial value function calculation, as shown in formula (7). When the sequence rank n is an odd number, the odd sequence is used to trigger the initial value of the Kent mapping, and when the sequence rank n is an even number, the even sequence is used to trigger the initial value of the Kent mapping. so that t n The output range is (0,1), which satisfies the requirement that the initial value range of the Kent map is (0,1).

[0024]

[0025] 7) Use odd mapping sequence x n or even mapping sequence y n Perform optimal function processing, when k=0, the odd mapping sequence is output. When k=1, the even mapping sequence is output, and the output sequence is the preferred sequence.

[0026] 8) The sequence generated after the optimization is a real-valued sequence, and then the threshold function method is used to convert the real-valued sequence into a binary chaotic sequence, that is, the average value of the sequence is used as the threshold value of the threshold. If the real-valued sequence is greater than the threshold, the output is 1 , otherwise the output is 0.

PUM

Description & Claims & Application Information

We can also present the details of the Description, Claims and Application information to help users get a comprehensive understanding of the technical details of the patent, such as background art, summary of invention, brief description of drawings, description of embodiments, and other original content. On the other hand, users can also determine the specific scope of protection of the technology through the list of claims; as well as understand the changes in the life cycle of the technology with the presentation of the patent timeline. Login to view more.