Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Passive multi-source multi-target tracking method based on dynamic multidimensional allocation

A multi-target tracking and multi-dimensional allocation technology, applied in the field of passive multi-source multi-target tracking, can solve the problems of high algorithm time complexity and low correlation accuracy, reduce time complexity, improve data correlation accuracy, and realize effective tracked effect

Active Publication Date: 2017-05-31
HARBIN INST OF TECH
View PDF9 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The present invention proposes a passive multi-source multi-target tracking method based on dynamic multi-dimensional allocation in order to solve the problems of low correlation accuracy and high algorithm time complexity in the prior art

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Passive multi-source multi-target tracking method based on dynamic multidimensional allocation
  • Passive multi-source multi-target tracking method based on dynamic multidimensional allocation
  • Passive multi-source multi-target tracking method based on dynamic multidimensional allocation

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

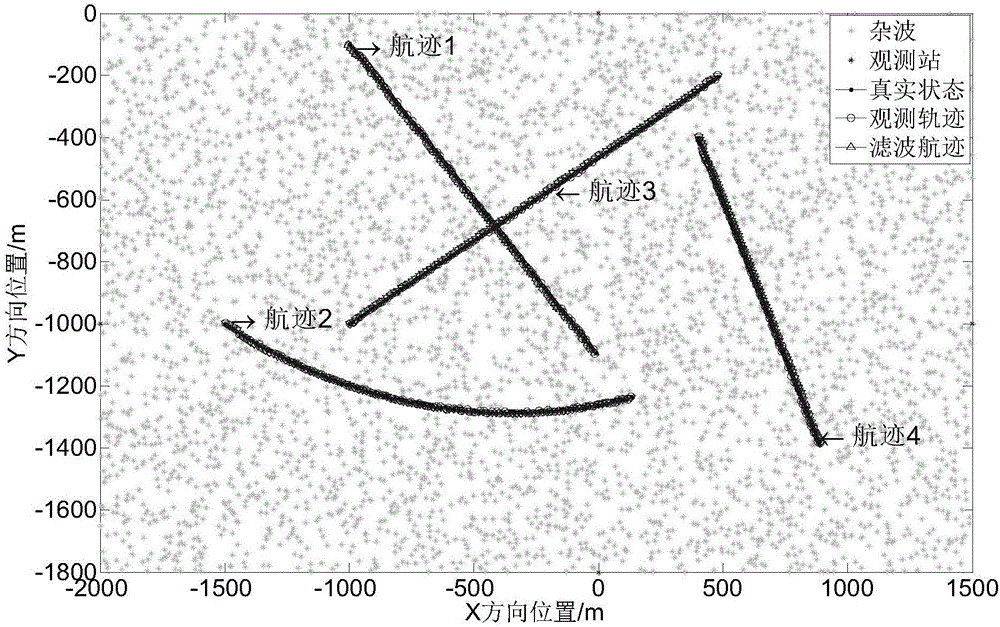
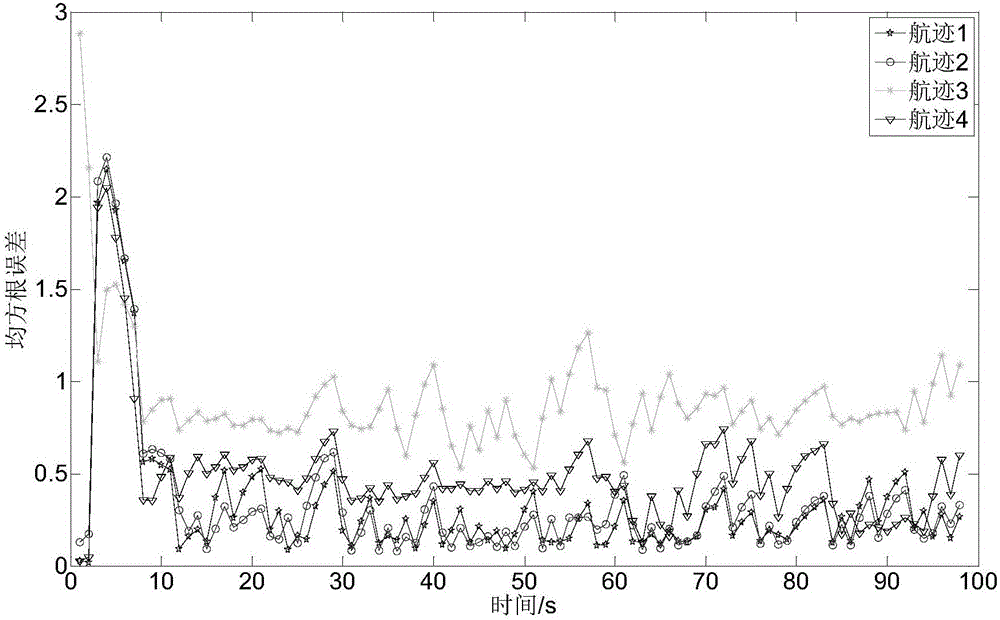
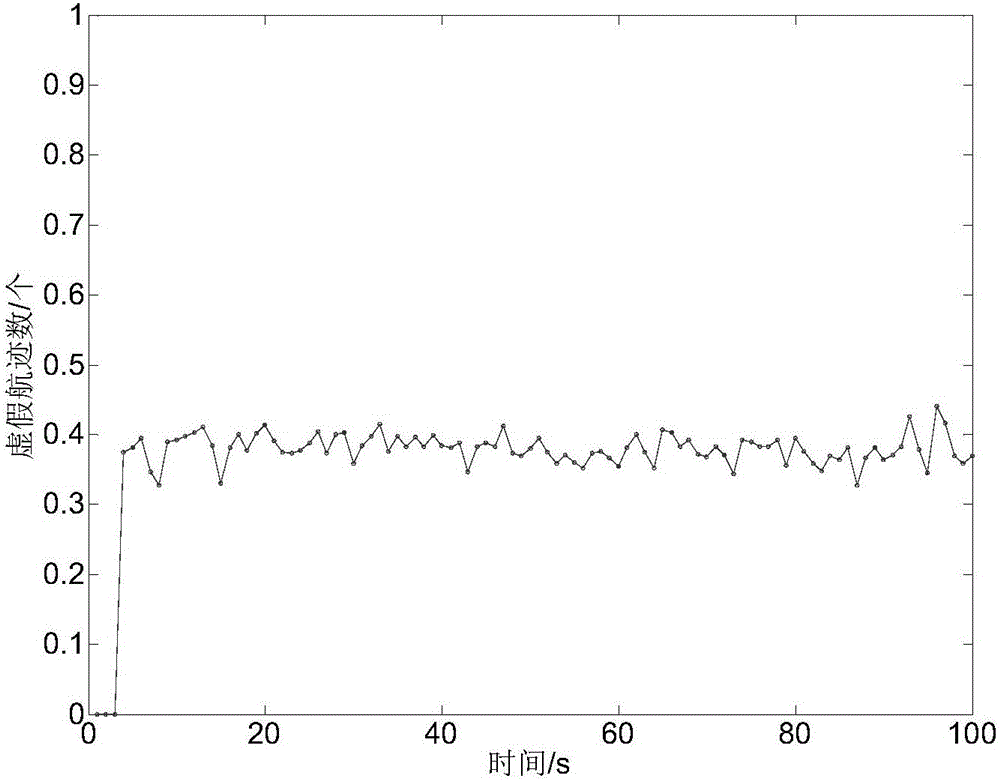
[0024] Specific implementation mode one: as Figure 5 As shown, a passive multi-source multi-target tracking method based on dynamic multi-dimensional allocation includes the following steps:

[0025] Step 1: Using the state of the target at time k-1, establish a preselected wave gate corresponding to the track p of the target

[0026] Step 2: Use the pre-selected gate constructed in Step 1 And the track p at time k-1 and the combination of observation values ​​of each sensor build cost function And construct a binary variable based on the one-to-one correspondence between the track p and the observed value

[0027] Step 3: Use the cost function constructed in step 2 and a binary variable Construct the global association cost function, obtain (S+1)-D distribution formula, and give constraint condition; The number of described S represents sensor, D represents dimension;

[0028] Step 4: Use the Lagrangian relaxation algorithm to relax the constraints of step 3, ...

specific Embodiment approach 2

[0035]Specific embodiment 2: The difference between this embodiment and specific embodiment 1 is that in the step 1, the state of the target at time k-1 is used to establish a pre-selected wave gate corresponding to the track p of the target The specific process is:

[0036]

[0037]

[0038]

[0039]

[0040]

[0041]

[0042]

[0043] in Indicates the estimated value of the target position at time k-1, Indicates the estimated value of the target speed at time k-1, h s (X) is the observation equation of sensor s, is h s (X) the partial derivative with respect to X, is the state transition function at time k, with are the estimated values ​​of the target state and the state covariance matrix at time k-1, respectively, with are the predicted values ​​of the target state and the state covariance matrix at time k, respectively, and the predicted value of the target state at time k can be obtained by predicting the target state at time k-1 ...

specific Embodiment approach 3

[0045] Embodiment 3: The difference between this embodiment and Embodiment 1 or 2 is that the pre-selected wave gate constructed in Step 1 is used in Step 2. And the track p at time k-1 and the combination of observation values ​​of each sensor build cost function And construct a binary variable based on the one-to-one correspondence between the track p and the observed value The specific process is:

[0046]

[0047]

[0048]

[0049]

[0050]

[0051]

[0052]

[0053] where the cost function represents the combination of observations Observations in derived from the objective cost, represents the combination of observations from the target probability, represents the combination of observations The probability of originating from the spurious signal source, represents the empty set, X p is the true value of the target state at time k, is the estimated value of the target state at time k, using the predicted value of the target st...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a passive multi-source multi-target tracking method based on dynamic multidimensional allocation, relates to the field of passive multi-source multi-target tracking and aims at solving the problems of low correlation accuracy of a target track and high time complexity of an algorithm in an existing passive multi-source multi-target tracking algorithm. The passive multi-source multi-target tracking method disclosed by the invention comprises the following steps: firstly, corresponding to a preselection wave gate of a track p of a target; secondly, constructing a cost function and a two-valued variable; thirdly, obtaining a (S+1)-D allocation formula and giving out constraint conditions; fourthly, carrying out dimension reducing processing on the (S+1)-D allocation formula to obtain a two-dimensional allocation formula; fifthly, calculating a dual solution of the two-dimensional allocation formula; sixthly, updating a lagrangian multiplier by using a subgradient vector; seventhly, obtaining an allocation combination of the track p and a corresponding observation value; eighthly, carrying out maximum likelihood estimation by using a likelihood function; ninthly, estimating a target state according to a kalman filtering method and updating the track by using a state estimating value, thus realizing multi-target tracking. The passive multi-source multi-target tracking method disclosed by the invention is applied to the fields of aviation and airborne radar.

Description

technical field [0001] The invention relates to a passive multi-source and multi-target tracking method based on dynamic multi-dimensional distribution. Background technique [0002] In the field of multi-sensor multi-target tracking, it is a very challenging problem to determine which target an observation in a sensor comes from, that is, the data association problem. This has been extensively studied starting in the 1960s, and a family of algorithms have been developed that vary in complexity and tracking performance. In the multi-passive sensor multi-target tracking application scenario, since the sensor can only obtain the angular observation data of the target, but cannot obtain complete target position information, the pure angular data association at this time is undoubtedly quite challenging. [0003] In recent years, methods to solve the problem of multi-sensor multi-target data association include nearest neighbor (NN), joint probabilistic data association (JPDA) ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01C21/20G01C23/00
CPCG01C21/20G01C23/00
Inventor 周共健卜石哲
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com