Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Nonlinear system state deviation evolution method based on differential algebra and Gaussian sum

A technique of nonlinear systems and differential algebra, applied in the field of nonlinear system state and its deviation prediction

Active Publication Date: 2017-11-28
NAT UNIV OF DEFENSE TECH
View PDF4 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At present, there is no research or application results on the application of this method for nonlinear dynamic system deviation prediction in China.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Nonlinear system state deviation evolution method based on differential algebra and Gaussian sum
  • Nonlinear system state deviation evolution method based on differential algebra and Gaussian sum
  • Nonlinear system state deviation evolution method based on differential algebra and Gaussian sum

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

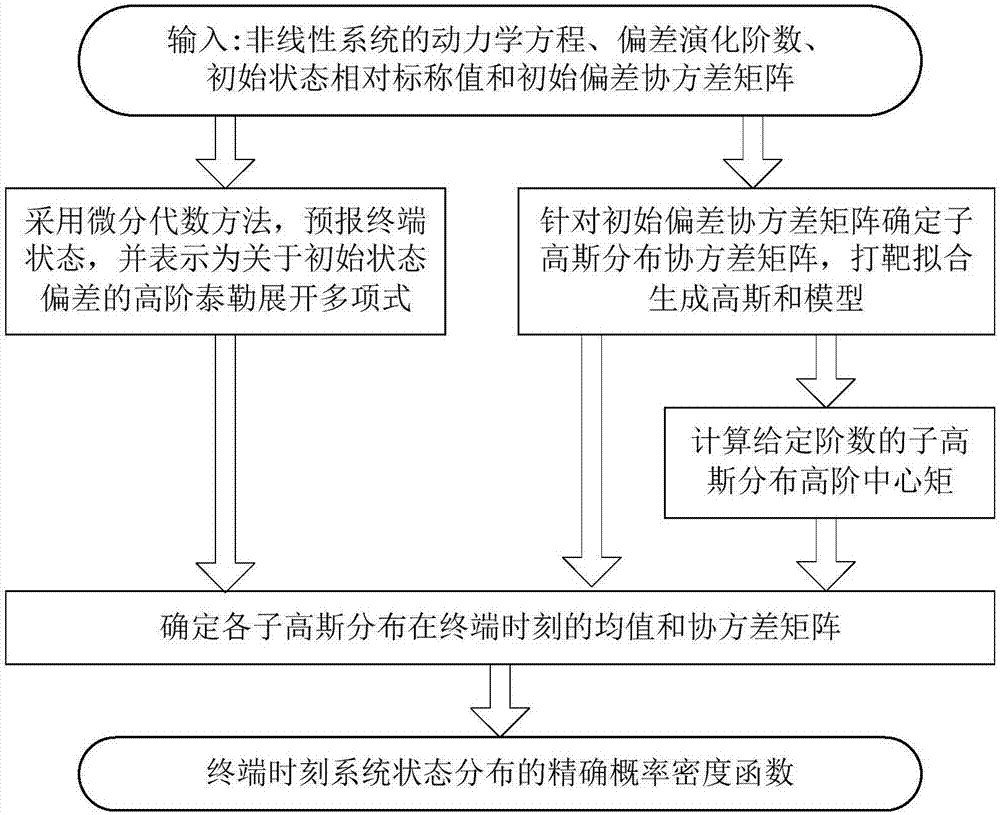
[0097] Such as figure 1 As shown, in this embodiment, the steps of the nonlinear system state deviation evolution method based on differential algebra and Gaussian sum include:

[0098] 1) Input the dynamic equation of the nonlinear system, the evolution order N of the deviation, and the relative nominal value of the initial state and the initial bias covariance matrix P 0 ;

[0099] 2) Using the differential algebra method to predict the terminal state of the nonlinear system according to the dynamic equation of the nonlinear system, and express it as the initial state deviation δx 0 Higher-order Taylor expansion polynomials of ;

[0100] 3) For the initial bias covariance matrix P 0 Determine the sub-Gaussian distribution covariance matrix P i , for a sub-Gaussian distribution covariance matrix P i The multiple sub-Gaussian distributions in the target are used to fit the initial deviation distribution to generate a Gaussian sum model;

[0101] 4) Calculate the high-o...

Embodiment 2

[0191] The process of this embodiment is basically the same as that of Embodiment 1, and its main difference is:

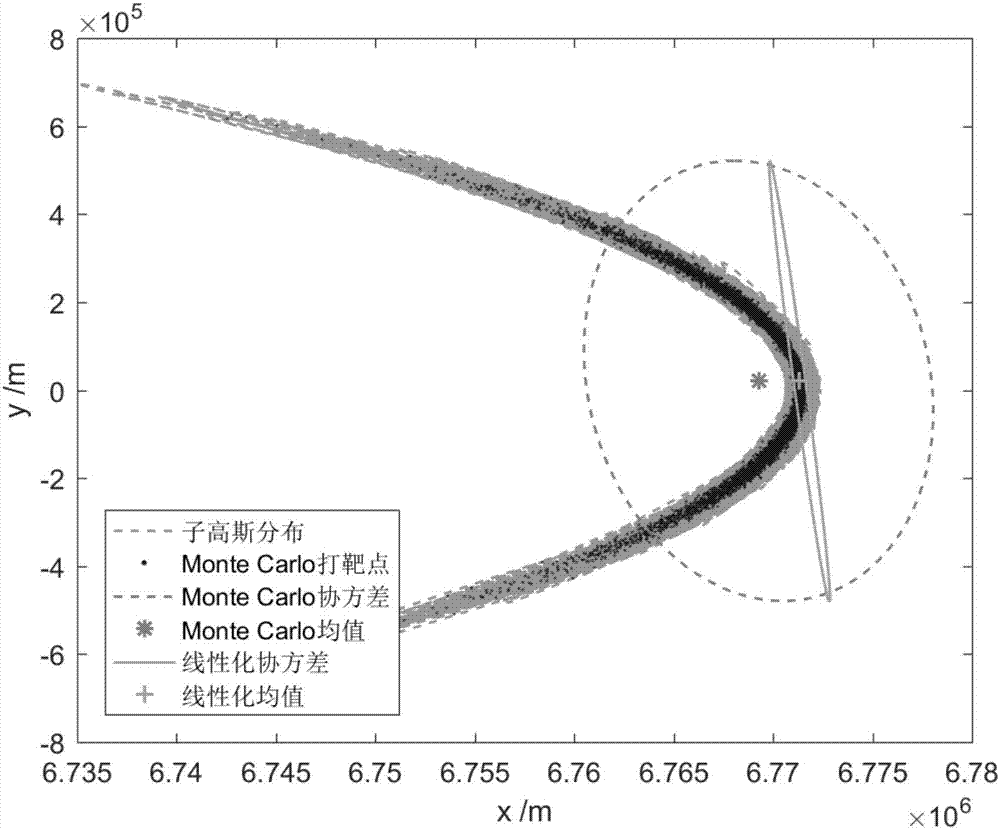
[0192] In step 2.1), the nonlinear system is the nonlinear relative trajectory of the spacecraft in geostationary orbit considering the solar light pressure, the system dimension n=6, and the state variable x is the relative position of the slave spacecraft in the orbital coordinate system of the master spacecraft and velocity vector, ie x=[r T v T ] T , where r=[x,y,z] T is the relative position vector, v=[v x ,v y ,v z ] T is the relative velocity vector.

[0193] In this embodiment, the dynamic equation of the nonlinear system is in the form of an ordinary differential equation, and the terminal state is obtained by the Runge-Kutta integration method with variable step size.

[0194] In this embodiment, the specific expression of the dynamic equation of the nonlinear system is:

[0195]

[0196] Wherein, a is the semi-major axis of the main spacecr...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a nonlinear system state deviation evolution method based on differential algebra and Gaussian sum. The method includes forecasting the terminal state of a nonlinear system according to a differential algebra method, and representing it as a high-order Taylor expansion polynomial related to original-state deviation; determining a sub Gaussian distribution covariance matrix, and fitting a Gaussian sum model for each sub Gaussian distribution through shooting; calculating the high-order central moment of the sub Gaussian distributions; determining the mean value and the covariance matrix of each sub Gaussian distribution at the terminal moment, and providing a terminal-state deviation distribution probability density function in the form of the Gaussian sum. The method can be extended to any designated-order deviation evolution accuracy automatically, manual derivation of high-order partial derivatives of kinetic equations is not needed, the method is applicable to long-term forecasted nonlinear system deviation evolution analysis problems with high nonlinearity, the remarkable efficiency advantages of the method can be still maintained as compared to the Monte Carlo simulation method while deviation distribution and non-Gaussianity thereof are described accurately, and accordingly, the method has the advantages of convenience in use and high calculation accuracy.

Description

technical field [0001] The invention relates to the field of spacecraft orbital dynamics, in particular to a nonlinear system state deviation evolution method based on differential algebra and Gaussian sum, which is used for the state and deviation prediction of the nonlinear system. Background technique [0002] The spacecraft trajectory deviation evolution technology is an important basic technology for space collision warning, spacecraft orbit determination, navigation filtering, and spacecraft trajectory safety analysis and design. The prediction accuracy of trajectory deviation directly affects the credibility of early warning, orbit determination and navigation results, and even determines the success or failure of space missions. Since the essence of the spacecraft orbital dynamics model is a nonlinear system in the form of ordinary differential equations or state transition equations, the essence of the spacecraft trajectory deviation evolution problem is the nonline...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/11G06F17/13G06F17/16
CPCG06F17/11G06F17/13G06F17/16
Inventor 罗亚中孙振江张进杨震
Owner NAT UNIV OF DEFENSE TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com