Seismic data reconstruction method based on spatial constrained compressed sensing

A seismic data and compressed sensing technology, applied in seismology, seismic signal processing, geophysical measurement, etc., can solve the problems of lack of frame continuity information, difficult selection of seismic data sparse base, reconstruction data sparsity and low reconstruction efficiency.

Active Publication Date: 2019-03-19
NORTH CHINA ELECTRIC POWER UNIV (BAODING)
View PDF4 Cites 15 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0008] In order to solve the problem that the traditional seismic data reconstruction algorithm needs to meet the limitation of Nyquist sampling theorem, it is difficult to select the sparse base of seismic data reconstruction using compressed sensing algorithm and the lack of fra

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Seismic data reconstruction method based on spatial constrained compressed sensing
  • Seismic data reconstruction method based on spatial constrained compressed sensing
  • Seismic data reconstruction method based on spatial constrained compressed sensing

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0058] The embodiments will be described in detail below in conjunction with the accompanying drawings.

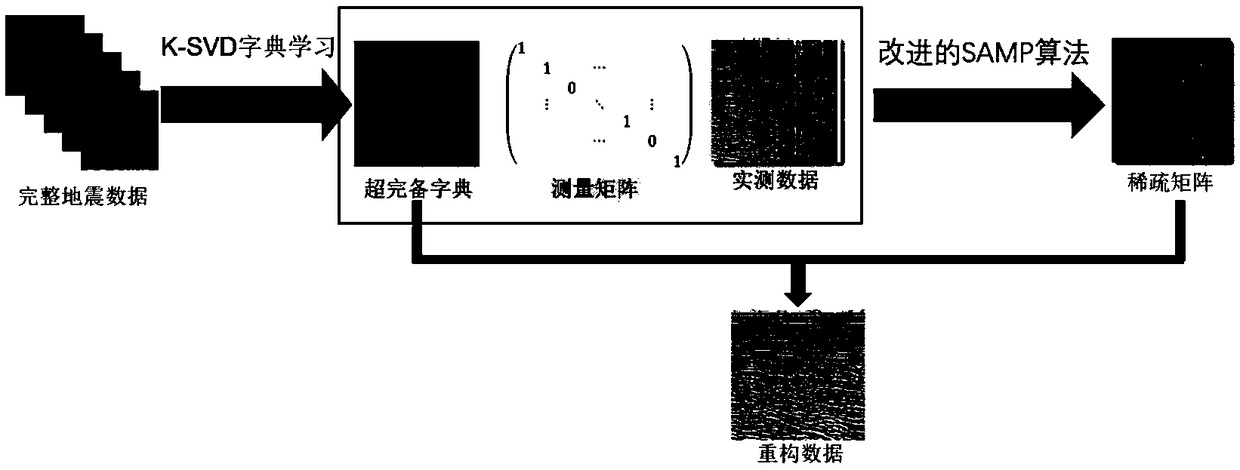
[0059] A. Compressed Sensing Algorithms with Spatial Correlation

[0060] Seismic data reconstruction based on compressed sensing can be expressed as:

[0061] y=Φf (1)

[0062] Where: y∈R M is the incomplete seismic data collected, f∈R N is the original complete seismic data (MM×N is the observation matrix. Use overcomplete dictionaries Sparse representation of the complete seismic data f can be expressed as:

[0063]

[0064] In the formula, the number K of non-zeros in the sparse solution x is much smaller than N, and then the incomplete seismic data y collected is obtained through the observation matrix Φ, expressed as

[0065] y=θx (3)

[0066] In the formula, the sensing matrix Φ and Irrelevant, and finally reconstruct the seismic data, that is,

[0067]

[0068] is an estimate of x. Finally, the original seismic data is reconstructed by the fol...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention belongs to the technical field of oilfield seismic big data reconstruction, and particularly relates to a seismic data reconstruction method based on spatial constrained compressed sensing. The method comprises the steps that a part of data is taken as training data, K-SVD dictionary learning is used for training an overcomplete dictionary to reconstruct original earthquake data; a joint sparse decomposition method is used for extracting shared spatial information, and a sensing matrix in a compression sensing algorithm is transformed; a sparsity self-adaptive matching tracking algorithm is improved, an initial sparsity estimation method is introduced, and the data is reconstructed by adopting a variable step size strategy. The reconstructed result not only is clear in detail, but also greatly reduces the operation time compared with IRLS and SAMP, and the horizontal transition is smoother, which indicate that the designed algorithm utilizes spatial related information and the reconstructed result is more real.

Description

technical field [0001] The invention belongs to the technical field of oilfield seismic big data reconstruction, and in particular relates to a seismic data reconstruction method based on space-constrained compressed sensing. Background technique [0002] Data reconstruction is an important part of data processing. In the signal field, the signal data collected due to factors such as environment, equipment, and human factors may not be complete. If incomplete data is used for data interpretation and analysis, there will be large deviations in the analysis results, so the data needs to be reconstructed before data interpretation and analysis. In addition, for seismic exploration, a large amount of data acquisition work, a large amount of data will generate huge costs in various links such as acquisition, storage and transportation. Therefore, on the one hand, it is hoped to reduce the collected data as much as possible, and on the other hand, it is hoped that the reconstruc...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G01V1/30
CPCG01V1/307
Inventor 石敏朱震东朱登明
Owner NORTH CHINA ELECTRIC POWER UNIV (BAODING)
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap