Supercharge Your Innovation With Domain-Expert AI Agents!

Model order determination method based on S-shaped function random subspace identification

A random subspace and function technology, applied in the field of model order determination based on S-type function random subspace identification, can solve the problems of model order misjudgment, index insensitivity, etc., to improve accuracy and avoid modal omission Effect

Active Publication Date: 2020-05-08
SOUTHEAST UNIV
View PDF2 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, all kinds of discriminant indicators that have been proposed are easily affected by

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Model order determination method based on S-shaped function random subspace identification
  • Model order determination method based on S-shaped function random subspace identification
  • Model order determination method based on S-shaped function random subspace identification

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

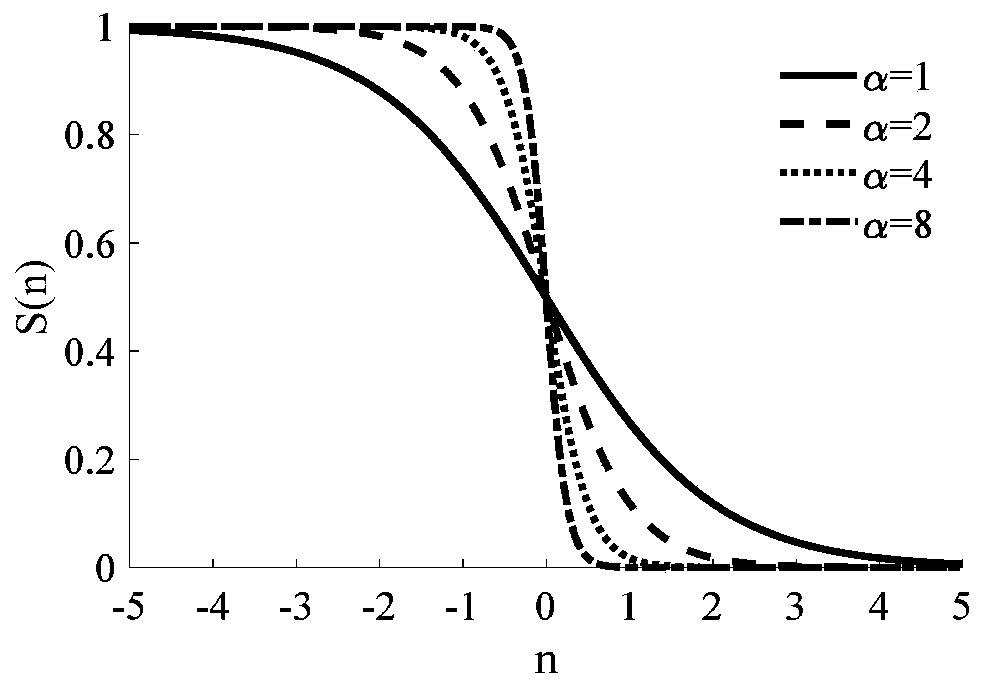
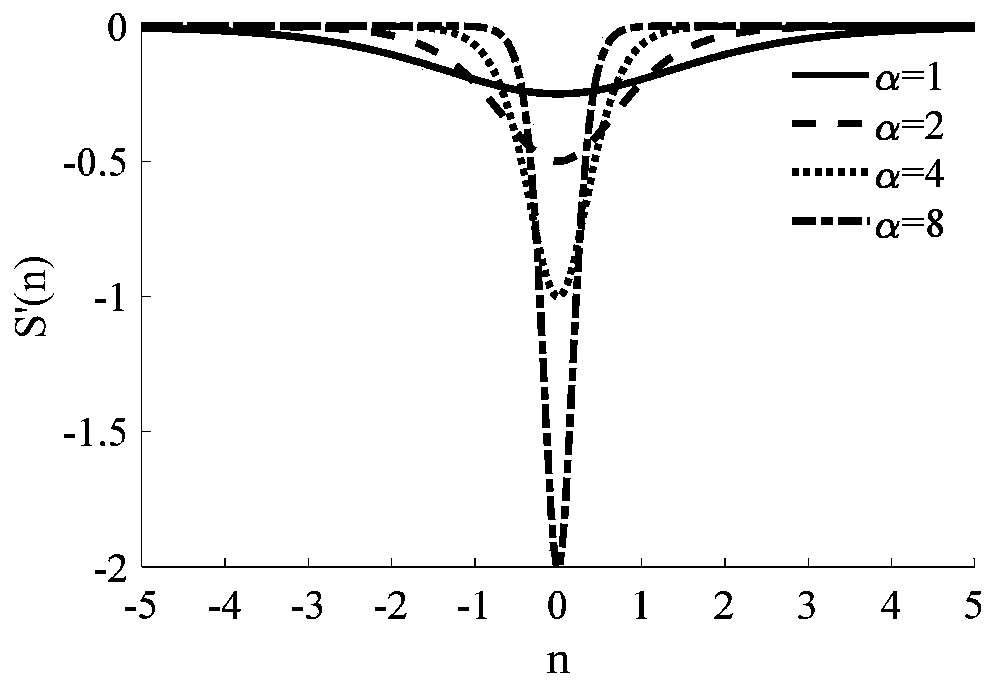
[0034] Such as figure 1 , shown in Fig. 2 (a) and Fig. 2 (b), a kind of model order determination method based on sigmoid function random subspace identification comprises the following steps:

[0035] (1) for Figure 4 For the vibration system shown, the Hankel matrix can be established by the following formula, where Y p is the first i×M rows of the Hankel matrix, Y f is the last i×M row of Hankel matrix, y k is a column vector composed of the dynamic responses of all measuring points at k sampling time. M is the number of structural dynamic response measuring points, i can be j is usually 20i, and the symbol [·] represents the rounding operation.

[0036]

[0037] (2) Carry out matrix projection calculation to Hankel matrix according to the following formula, obtain projection matrix P;

[0038]

[0039] (3) Singular value decomposition is performed on the projection matrix, and the singular values ​​obtained by the decomposition are arranged in descending orde...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a model order determination method based on S-shaped function random subspace identification. The method comprises the following steps: establishing a Hankel matrix according to a measured structural dynamic response; performing matrix projection calculation on the Hankel matrix to obtain a projection matrix P; carrying out singular value decomposition on the projection matrix, and arranging singular values obtained through decomposition in a descending order; normalizing the singular value sequence arranged in a descending order, and converting singular values to a closed interval of [epsilon, 1-epsilon]; carrying out nonlinear least square fitting on the relationship between the normalized singular value and the order by adopting an S-shaped function in a proper order interval; according to an S-shaped function obtained through fitting, solving a tangent line passing through (n0, 0.5), and then further solving an intersection point (n *, 0) of the selected tangent line and a horizontal axis, so that the model order N of the random subspace is 2. [n *]. The bad influence of a modal omission phenomenon and model order over-estimation on modal parameter identification can be effectively avoided, the method can be applied to adaptive model order determination of various vibration structures, and the accuracy of random subspace identification can be improved.

Description

technical field [0001] The invention relates to the technical field of modal parameter analysis, in particular to a model order determination method based on Sigmoid function random subspace identification. Background technique [0002] Structural health monitoring has very important practical significance for the maintenance and management of civil engineering structures. The real operation of the structure can be obtained through the long-term monitoring of the structure by the health monitoring system. Among them, modal parameter analysis is an important prerequisite for structural damage identification and state assessment based on dynamic characteristics, and is of great significance for structural health monitoring. [0003] The random subspace identification method is a time-domain modal parameter identification method with excellent effect, and has been successfully applied to the modal parameter analysis of various vibrating structures. However, there are still man...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/16G06F17/15
CPCG06F17/16G06F17/15Y02T90/00
Inventor 廖聿宸宗周红吴睿钱海敏杜孟林
Owner SOUTHEAST UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com