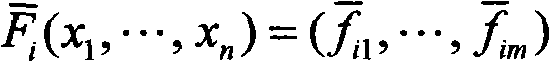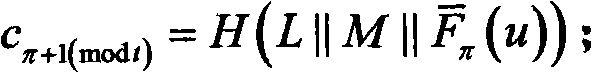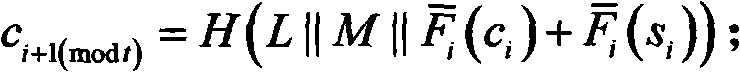Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Ring signature method for anonymizing information based on algebra

A ring signature and message technology, applied to the public key and key distribution of secure communication, can solve the problem of insecure ring signature system

Inactive Publication Date: 2013-03-13
XIAN UNIV OF TECH
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0010] The purpose of the present invention is to provide an algebra-based method for anonymous ring signature of messages, which solves the defect that the existing ring signature system is not safe under quantum computing

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Ring signature method for anonymizing information based on algebra
  • Ring signature method for anonymizing information based on algebra
  • Ring signature method for anonymizing information based on algebra

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0132] Anonymous ring signature scheme based on multi-variable public key cryptography oil-vinegar signature system:

[0133] Step 1. Generate System Parameters

[0134] 1) Set k=GF(q) to be a finite field characterized by p=2, where q=2 8 ;

[0135] 2) make o=30, v=64, m=30 is the number of equations in the multivariate equation system, and n=o+v=94 is the number of variables;

[0136] 3) Select H: {0, 1} * →k 30 A cryptographically secure collision-resistant one-way irreversible hash function. The system parameters are (k, q, p, l, m, n, H).

[0137] Step 2. Key generation

[0138] 1) Suppose there are t users in the ring, set U={u 0 , u 1 ,..,u t-1},

[0139] According to the multivariate public key cryptosystem, each user u i (0≤i≤t-1) randomly select F i is from k n to k m The reversible Oil-Vinegar polynomial map, Oil-Vinegar polynomial has the following form:

[0140] F i = Σ ...

Embodiment 2

[0173] Anonymous ring signature scheme based on multivariable public key cryptography Square+ signature system:

[0174] The square+ system is a multivariate polynomial system based on a singular characteristic field, which has relatively high security and can resist quantum computer attacks, and has high encryption and decryption efficiency. We combine the square+ system and propose a ring signature scheme based on the square+ system.

[0175] 1. The structure of Squaare+ system

[0176] Let k be a finite field of order q, where q≡3mod4. is the n+l expansion of k, where l makes n+l odd. F is the mapping from K to K, F(X)=X 2 , where X∈K.

[0177] Randomly choose an injective affine map L 1 :k n →k n+l ;d quadratic polynomials with n+l variables

[0178] g 1 ,..., g d ∈k[x 1 ,...,x n+l ]

[0179] and an invertible affine map L 2 :k n+l+d →k n+l+d . φ: K→k n+l , is an isomorphic map of vector spaces:

[0180]

[0181] Since φоFоφ -1 is a quadratic polyno...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a ring signature method for anonymizing information based on algebra, comprising the following steps: generating system parameters, generating a secret key, generating the ring signature and verifying the ring signature. The ring signature method based on the traditional cryptosystem is subjected to security threat under the quantum computer while the ring signature method based on the multivariate public key cryptosystem solves the problem that the existing ring signature systems are insecure under the quantum computation. The method has the advantages of security and high computing efficiency.

Description

technical field [0001] The invention belongs to the technical field of information security, and relates to an algebra-based method for signing a message anonymous ring. Background technique [0002] In 2001, under the background of how to leak secrets anonymously, Rivest et al. proposed a new signature technology called ring signature. Ring signature can be regarded as a special group signature, which has no trusted center and no group establishment process. The group here refers to the set composed of multiple possible signers, also known as the ring. The establishment of the ring is spontaneous, that is, the ring is established by a signer without consulting with others. A ring signature on an electronic document is signed by a signer on behalf of all members of the ring, but the signer is completely anonymous to the signature verifier. Ring signatures provide a neat way to reveal secrets anonymously. The unconditional anonymity of ring signatures is very useful in som...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/32H04L9/08H04L9/30
Inventor 王尚平马瑞
Owner XIAN UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com