Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for reconstructing curved surface of complex space

A technology of surface reconstruction and space, applied in image data processing, 3D modeling, instruments, etc., can solve problems such as surface reconstruction of complex geological structures, and achieve the effect of ensuring fast processing and ensuring accuracy

Inactive Publication Date: 2011-10-19
UNIV OF ELECTRONIC SCI & TECH OF CHINA
View PDF2 Cites 45 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0021] In order to overcome the above-mentioned shortcomings of the prior art, the present invention provides a method for surface reconstruction in complex spaces, which can solve the problem of layer interpolation under complex geological structures, thereby solving the problem of surface reconstruction in complex geological structures

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for reconstructing curved surface of complex space
  • Method for reconstructing curved surface of complex space
  • Method for reconstructing curved surface of complex space

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0064] First define some basic geological structures and terms used in this plan:

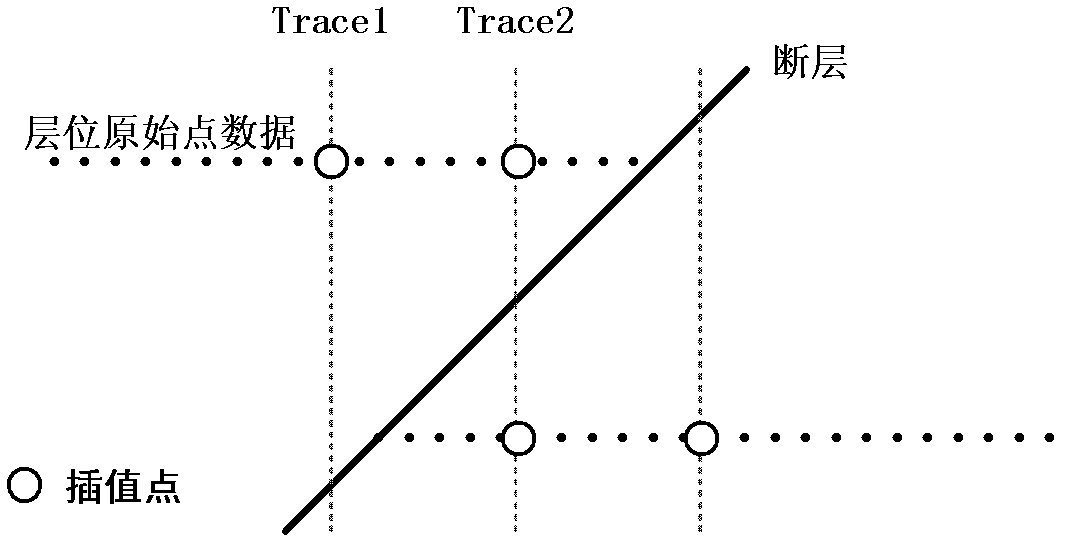
[0065] Horizon: It refers to a specific position in the stratigraphic sequence. The stratigraphic horizon can be the boundary of a stratigraphic unit, or it can be a marker layer belonging to a specific era, etc.

[0066] Fault: The crustal rock layer ruptures due to the force reaching a certain strength, and the structure that moves obviously relative to the rupture surface is called a fault.

[0067] Vertical fault: A fault with a small fault throw.

[0068] Gridding: Logically divide the discrete point data to form a regular logical grid, which is convenient for horizon interpolation.

[0069] Interpolation: The process of using known points to calculate unknown points.

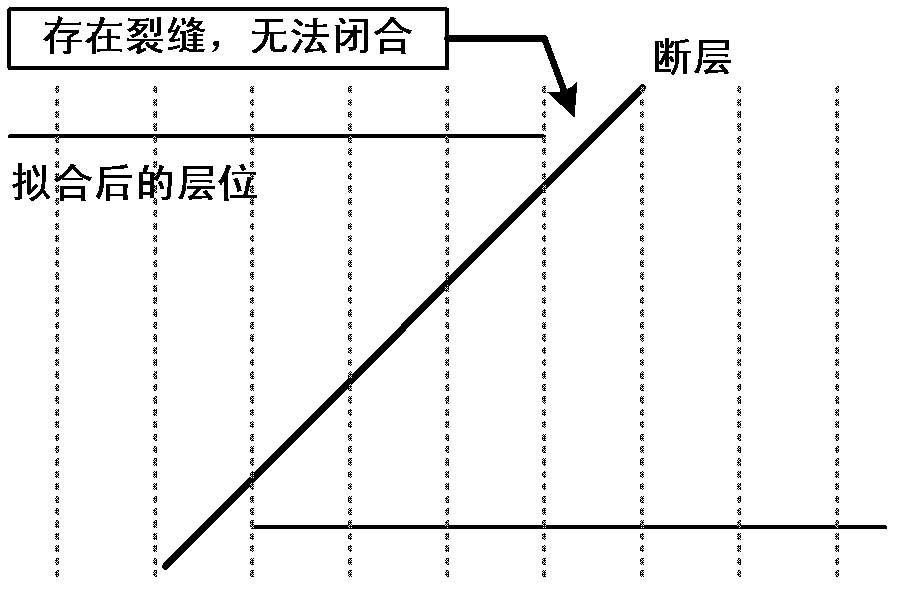
[0070] Fitting: A process of using the data after horizon interpolation to form horizons.

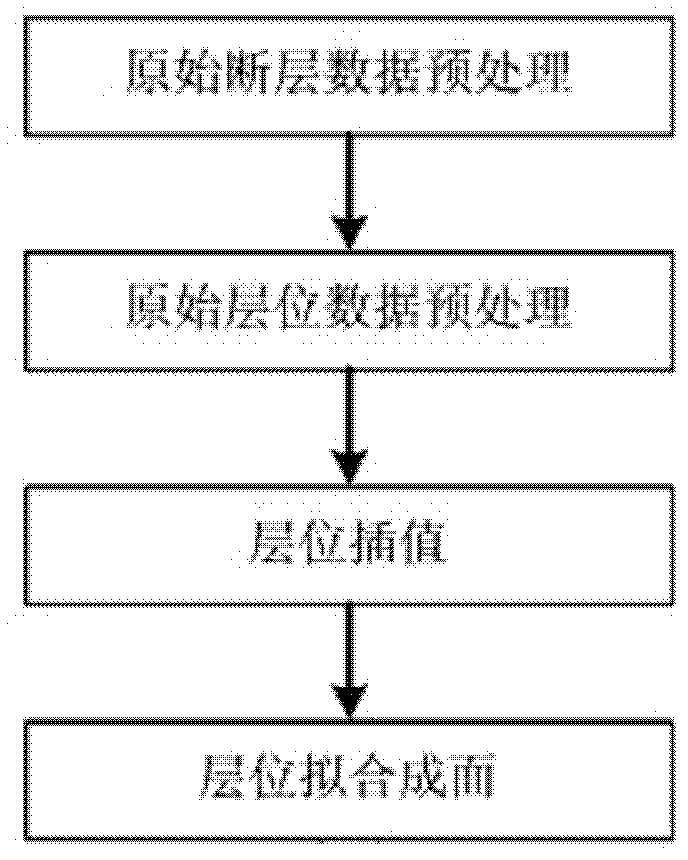
[0071] Such as image 3 As shown, a complex space surface reconstruction method includes the following steps:

[0...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for reconstructing curved surface of complex space that solves the layered curved surface reconstruction problem existed in the complex geologic structure of three-dimensional geological modeling by adopting complex space curved surface interpolation method and provides new ideas for the isoline drawing and geological block forming. The invention has the advantages that: the method solves the layer interpolation problem existed in the complex geologic structure, not only supports the positive and reverse faults as well as the vertical fault, but also is suitable for the multiple applications of geologic modeling; by adopting the layer fitting under the limitation of the polygonal borders of the faults, the seamless fitting of the layers and the faults is realized and the difficult problem that a conventional grid interpolation scheme layer position cannot be strictly crossed with the faults is solved; and by adopting the method of mixing with the grid layer interpolation, the method not only ensures the fast data treatment, but also ensures the fitting precision.

Description

technical field [0001] The invention relates to a method for reconstructing curved surfaces in complex spaces. Background technique [0002] Space surface reconstruction is widely used in various scientific research and engineering design such as CAD, computer graphics, meteorology and exploration. Due to the irregularity of the surface and the lack of clear rules and disorder of the scattered data, it is difficult to express the surface in a single mathematical form, so the interpolation method is generally used to reconstruct the surface. Space surface reconstruction uses computer technology to perform surface interpolation, thereby approximately restoring the real surface. Its essence is to use three-dimensional discrete points to fit the surface. [0003] Spatial surface reconstruction has important applications in the editing and display of unstructured data such as geological exploration data, logging data and reservoir data. In the field of geological exploration, t...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06T17/05
Inventor 鲁才陈凯云胡光岷
Owner UNIV OF ELECTRONIC SCI & TECH OF CHINA
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com