Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Self-paced matrix decomposition method based on Pareto optimization

A matrix decomposition and matrix technology, applied in genetic models, instruments, computing models, etc., can solve problems such as poor matrix decomposition and local minima

Inactive Publication Date: 2017-06-20
XIDIAN UNIV
View PDF0 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0010] The purpose of the present invention is to overcome the existing problems of self-paced learning in the self-paced matrix factorization method in the prior art, and effectively alleviate the problem of matrix factorization falling into a bad local minimum due to the non-convex objective function, especially when there are abnormal data and missing data in the case of

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Self-paced matrix decomposition method based on Pareto optimization
  • Self-paced matrix decomposition method based on Pareto optimization
  • Self-paced matrix decomposition method based on Pareto optimization

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

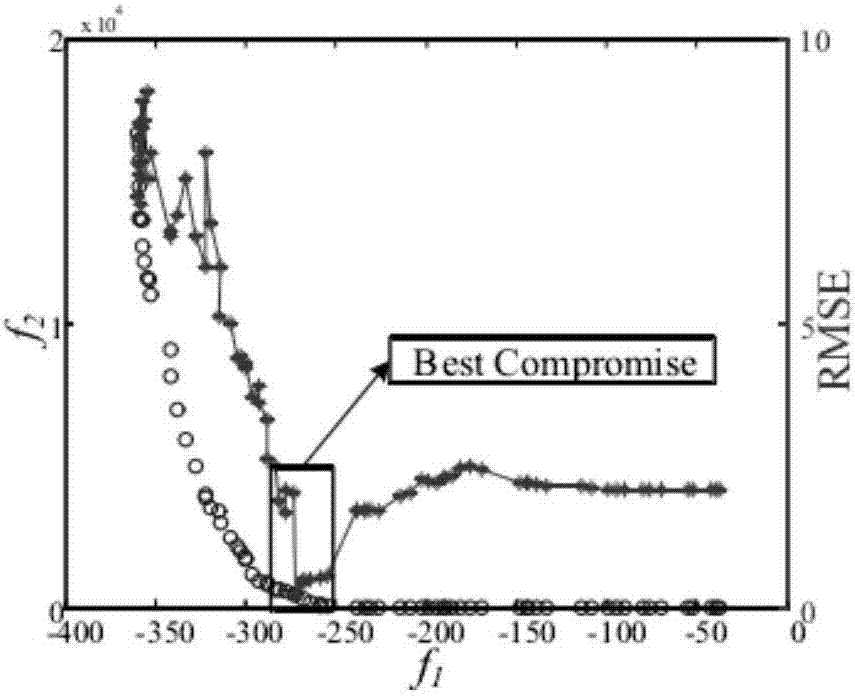
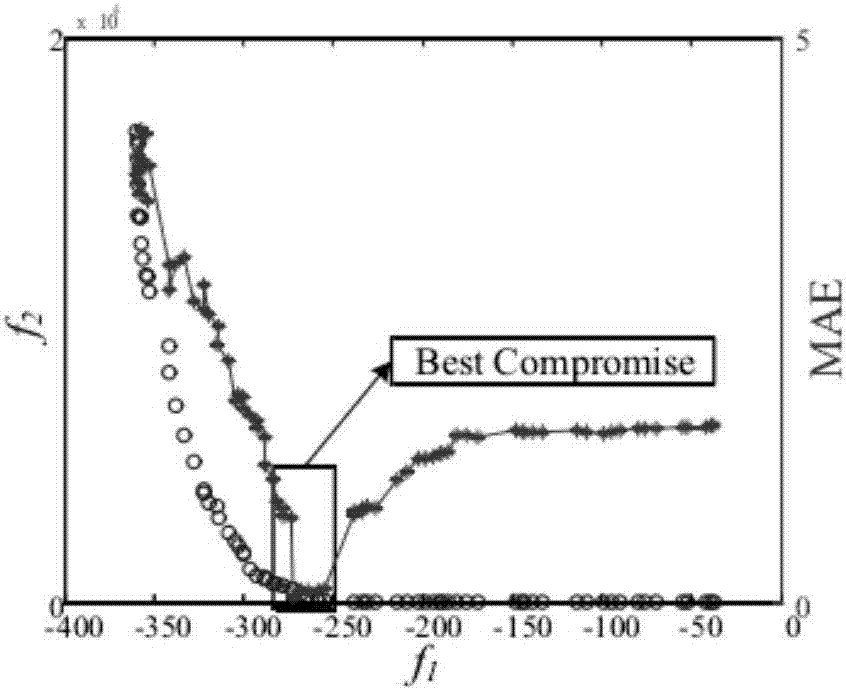
[0039] This embodiment provides a figure 1 The self-stepping matrix factorization method based on Pareto optimization shown includes the following steps:

[0040] Step 1) Input the matrix Y∈R to be decomposed m×n , population size N p and step size information, the matrix index set of the non-missing data in the matrix Y to be decomposed is Ω, and the step size information includes the initial step size k 0 and step increment μ;

[0041] Step 2) Decompose the matrix Y to be decomposed to obtain the initial matrix U 0 ,V 0 , calculate the matrix element loss value, and then according to the weight distribution method f(w ij ; k) and random method to generate a population size of N p The initial weight population P 0 And calculate the two objective function values ​​corresponding to the population individual, at this time And set the iteration termination number G max , where U 0 ∈R m×r ,V 0 ∈R r×n ,r0 Increase μ successively to get, w ij Indicates the weight of t...

Embodiment 2

[0052] On the basis of Embodiment 1, this embodiment provides a self-step matrix decomposition method based on Pareto optimization, including the following steps:

[0053] Step 1) Input matrix Y, population size N p and step information:

[0054] Randomly generate elements Y of matrix Y ij Obey the Gaussian distribution N(0,1), and then 40% of them are selected as missing data, 20% of the data is added to the uniformly distributed noise disturbance on [-20,20] and 20% of the data is added to Gaussian noise ~ N(0,0.01) Disturbance; step size information includes initial step size k and step size increment μ;

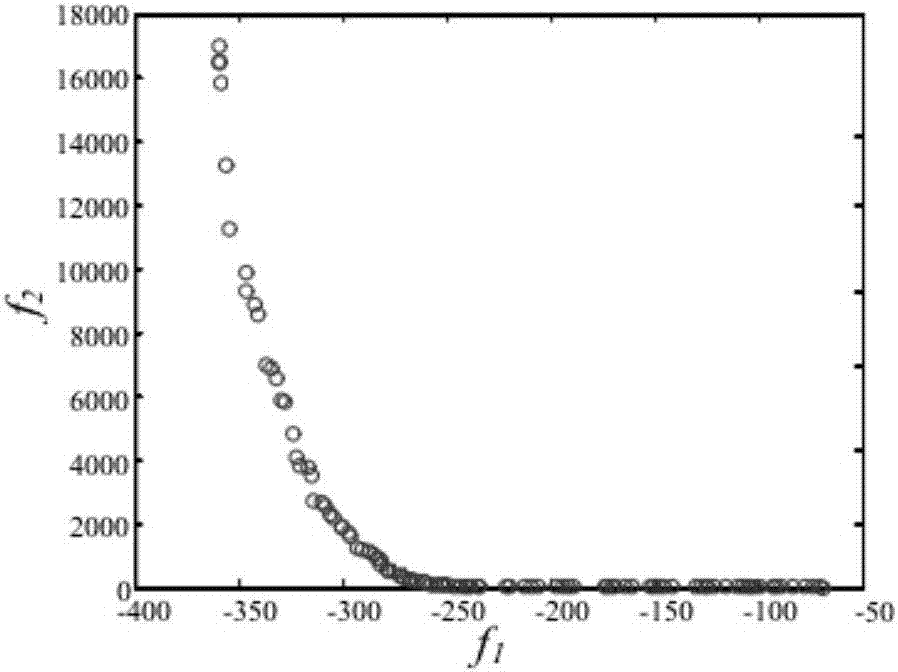
[0055] Step 2) Decompose Y to get the initial matrix U 0 ,V 0 , calculate the loss and generate the initial weight population P 0 And set the iteration termination number G max : Population P 0 Schematic figure 2 ;

[0056] Use the traditional matrix decomposition method to get the initial matrix U 0 ,V 0 , the matrix U 0 ,V 0 Substituting the loss function ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a self-paced matrix decomposition method based on Pareto optimization, and the method comprises the steps: changing a method, which employs a monotone increasing learning step in the conventional self-paced learning to determine the weight of a sample, into a method of obtaining the weight of the sample through the technology of Pareto optimization; changing a sample weight expression range [0, 1] in the Pareto optimization process into a range [-1, 1], and enabling a difficult sample weight to exist in a reasonable distribution range, thereby guaranteeing the diversity; finally selecting a Knee point which achieves the best compromise on an optimization result PF plane as a matrix element weight, thereby speeding up the matrix decomposition process. In a word, the method is more reasonable and accords with the cognitive science in a better way.

Description

technical field [0001] The invention belongs to the technical field of machine learning, and in particular relates to a self-step matrix decomposition method based on Pareto optimization. Background technique [0002] In the field of machine learning, due to the increasingly complex problems to be solved, the optimization objective functions of many tasks are non-convex, which makes it easy to fall into a local optimum during the optimization process. Inspired by the fact that people and animals often learn simple knowledge first and then gradually learn difficult knowledge to achieve learning goals, Y.Bengio, J.Louradour, R.Collobert, and J.Weston in the literature "Curriculum learning" (ICML, 2009) proposed a learning strategy course learning (CL) based on machine learning. Its core idea is to define a "course" in which training samples gradually increase in training difficulty, and then let the model train the defined course. Experiments prove that CL is beneficial to ac...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06N3/00G06N3/12
CPCG06N3/006G06N3/12
Inventor 公茂果武越王聪聪马晶晶李豪刘嘉王善峰张普照
Owner XIDIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com