An image denoising neural network training architecture and a method of training the image denoising neural network

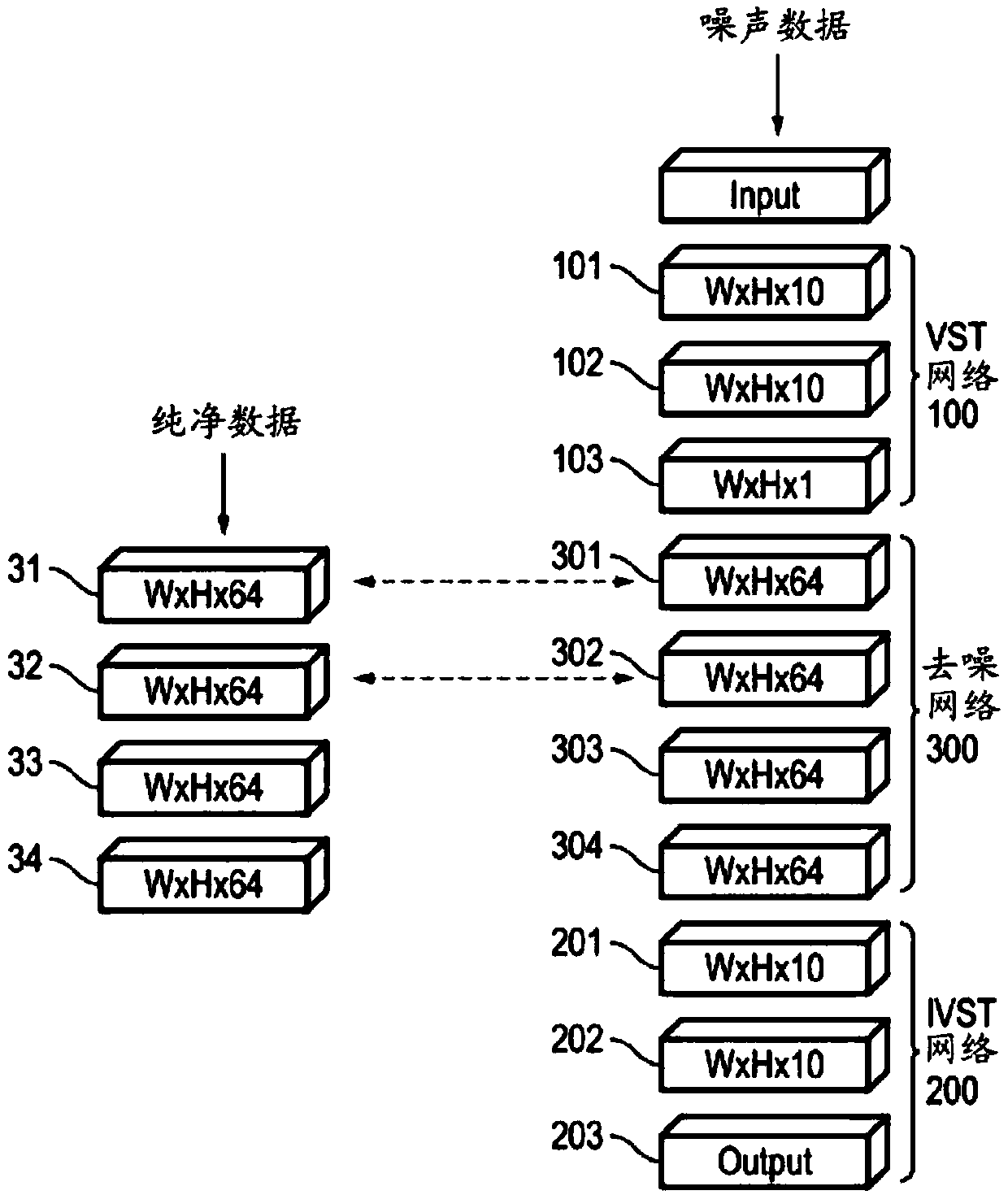
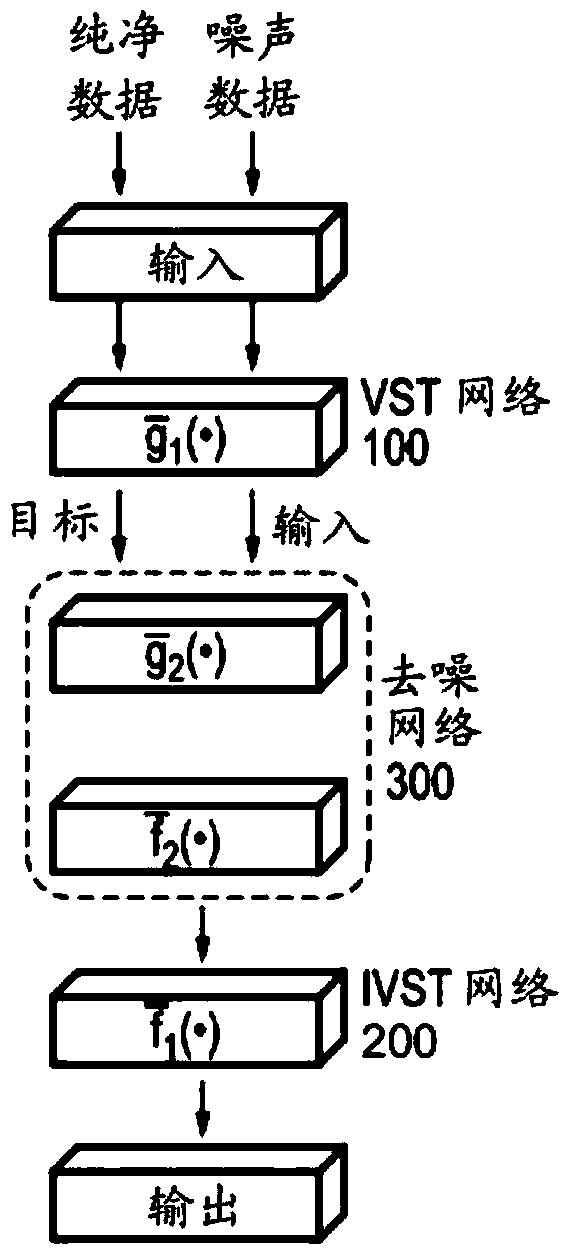
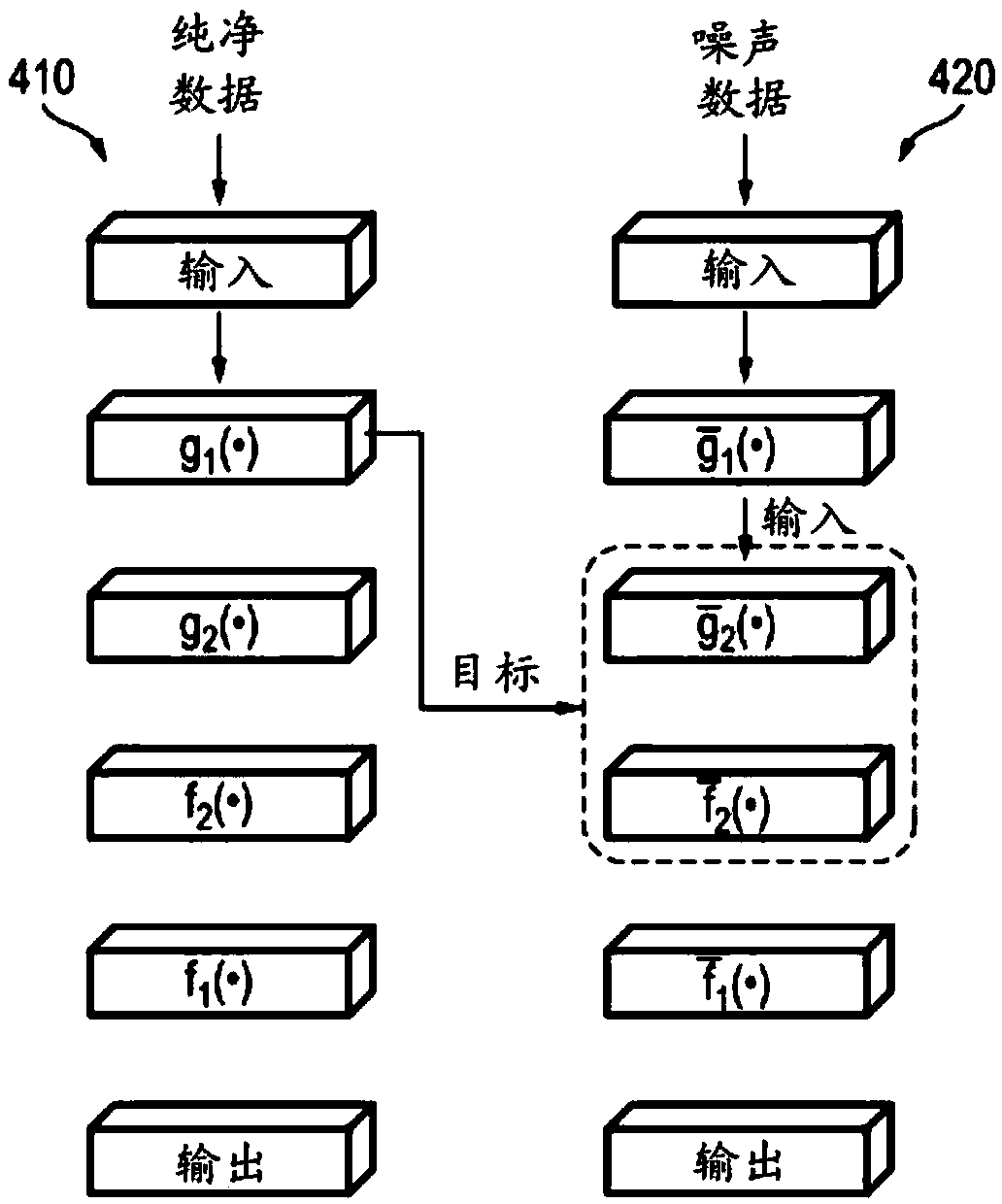
[0040] The present disclosure is directed to various embodiments of an image denoising neural network architecture and methods for training an image denoising neural network. In an exemplary embodiment, the image denoising neural network training architecture includes an image denoising neural network and a pure data neural network. The image denoising neural network and the pure data neural network can be configured to share information with each other. In some embodiments, the image denoising neural network may include a variance stabilization transformation (VST) network, an inverse variance stabilization transformation (IVST) network, and a denoising network between the VST network and the IVST network. The denoising network may include multiple convolutional autoencoders stacked on each other, and the VST network and the IVST network may each include multiple filter layers that together form a convolutional neural network.

[0041] Hereinafter, exemplary embodiments of the present disclosure will be described in more detail with reference to the accompanying drawings. However, the present disclosure may be embodied in various different forms, and should not be construed as being limited to the embodiments shown herein. On the contrary, these embodiments are provided as examples so that this disclosure will be thorough and complete, and will fully convey the aspects and features of this disclosure to those skilled in the art. Therefore, in order to fully understand the various aspects and features of the present disclosure, procedures, elements, and techniques that are not required for those of ordinary skill in the art may not be described. Unless otherwise stated, in all the drawings and written descriptions, similar reference numerals denote similar elements, and therefore, the description thereof may not be repeated.

[0042] It will be understood that although the terms "first", "second", "third", etc. may be used herein to describe various elements, components and/or layers, these elements, components and/or layers should not be affected by these Term limitation. These terms are used to distinguish one element, component or layer from another element, component or layer. Therefore, the first element, component or layer described below may be referred to as a second element, component or layer without departing from the scope of the present disclosure.

[0043] It will also be understood that when an element, component or layer is referred to as being "between" two elements, components or layers, it can be the only element between the two elements, components or layers, or one may also be present. Or multiple intermediate elements, components or layers.

[0044] The terminology used here is for the purpose of describing specific embodiments and is not intended to limit the present disclosure. As used herein, the singular forms "a" and "an" are also intended to include the plural forms, unless the context clearly dictates otherwise. It will also be understood that when used in this specification, the terms "comprising" and "including" designate the existence of stated features, wholes, steps, operations, elements and/or components, but do not exclude one or more other The existence or addition of features, wholes, steps, operations, elements, components, and/or groups thereof. That is, the processes, methods, and algorithms described herein are not limited to the operations indicated, and may include additional operations or may omit some operations, and the order of operations may vary according to some embodiments. As used herein, the term "and/or" includes any and all combinations of one or more of the associated listed items.

[0045] As used herein, the terms "substantially", "approximately" and similar terms are used as approximate terms rather than terms of degree, and are intended to illustrate the inherent nature of measured or calculated values ​​that one of ordinary skill in the art will recognize Variety. In addition, the use of "may" when describing an embodiment of the present disclosure means "one or more embodiments of the present disclosure." The terms "use", "being used" and "being used" as used herein may be considered as synonymous with the terms "utilizing", "being used" and "being utilized" respectively. In addition, the term "example" is intended to refer to an example or illustration.

[0046] Unless defined otherwise, all terms (including technical and scientific terms) used herein have the same meaning as commonly understood by those of ordinary skill in the art to which this disclosure belongs. It will also be understood that terms (such as those commonly defined in dictionaries) should be interpreted as having meanings consistent with their meanings in the context of related technologies and/or this specification, and should not be idealized or overly Interpreted in a formal sense, unless clearly defined in this article.

[0047] The processor, central processing unit (CPU), graphics processing unit (GPU), field-programmable gate array (FPGA), sensor according to embodiments of the present disclosure described herein , Capture devices, circuits, neural networks, filter layers, detectors, autoencoders, denoisers, encoders, decoders, and/or any other related devices or components, which can utilize any suitable hardware (for example, application specific integrated circuits) ), firmware, software and/or an appropriate combination of software, firmware and hardware. For example, various components of the processor, CPU, GPU, neural network, filter layer, detector, sensor, autoencoder, denoiser, encoder, decoder and/or FPGA can be integrated in (or implemented in) an integrated It is formed on an integrated circuit (IC) chip or on a separate IC chip. In addition, various components such as processors, CPUs, GPUs, neural networks, filter layers, detectors, sensors, autoencoders, denoisers, encoders, decoders and/or FPGAs can be used in flexible printed circuit films, carrier tapes It is implemented on a tapecarrier package (TCP), printed circuit board (PCB), or formed on the same substrate as the processor, CPU, GPU, and/or FPGA. In addition, the described actions, neural networks, filter layers, encoders, decoders, autoencoders, etc., may be one or more processors in one or more computing devices (for example, one or more CPUs and /Or processes or threads running on one or more GPUs, executing computer program instructions and interacting with other system components to perform the various functions described herein. The computer program instructions may be stored in a memory, which may be implemented in a computing device using a standard storage device such as, for example, random access memory (RAM). The computer program instructions can also be stored in other non-transitory computer readable media, such as, for example, CD-ROMs, flash drives, etc. Moreover, those skilled in the art should recognize that, without departing from the scope of the exemplary embodiments of the present disclosure, the functions of various computing devices may be combined or integrated into a single computing device, or the functions of a specific computing device may be distributed On one or more other computing devices.

[0048] figure 1 Shows an image denoising neural network training architecture (for example, a Poisson-Gaussian denoising training architecture) according to an embodiment of the present disclosure, and Figure 4 A method of training an image denoising neural network (for example, a Poisson-Gaussian denoising architecture) 20 according to an embodiment of the present disclosure is shown.

[0049] reference figure 1 In an embodiment of the present disclosure, the image denoising neural network includes a variance stabilization transformation (VST) neural network (for example, a convolutional variance stabilization network, a convolutional VST or a VST encoder) 100, an inverse variance stabilization transformation (IVST) A neural network (for example, an IVST decoder) 200 and a denoising network (for example, a stacked denoising autoencoder) 300 between the VST network 100 and the IVST network 200.

[0050] Each of the VST network 100 and the IVST network 200 may be a three-layer convolution neural network (CNN); however, the present disclosure is not limited thereto. In other embodiments, the VST network 100 and the IVST network 200 may have more than three layers or less than three layers. The VST network 100 and the IVST network 200 together can be considered as a Poisson denoiser. In some embodiments, the VST network 100 and the IVST network 200 may have the same number of layers. However, the present disclosure is not limited to this, and in other embodiments, the VST network 100 and the IVST network 200 may have a different number of layers with respect to each other.

[0051] The three-layer convolutional neural network of the VST network 100 may include the first filter layer 101 to the third filter layer 103, and the three-layer convolutional neural network of the IVST network 200 may include the first filter layer 201 to the third filter layer 203.

[0052] The first filter layer 101/201 may have a dimension of 3×3×1×10 (for example, pixel dimensions), the second filter layer 102/202 may have a dimension of 1×1×10×10, and the third filter layer 103 /203 may have a dimension of 1×1×10×1. The first filter layer 101/201 has 3×3 dimensions to utilize a binning operation, which includes summing the pixels in a small area (for example, a 3×3 pixel area) of the image before processing the image through the VST network 100 Or take its weighted average. The first filter layer 101/201 may be a convolution kernel having a 2D dimension of 3×3, and the second filter layer 102/202 may be a rectifier having a dimension of 1×1 (for example, a rectified linear unit or ReLU (rectified linear unit) , Rectification linear unit)), and the third filter layer 103/203 may be another rectifier having a dimension of 1×1.

[0053] In the VST network 100 and the IVST network 200, the rectified linear function can be applied to the output of the first filter layer 101/201 and the second filter layer 102/202. For example, each of the first filter layer 101/201 and the second filter layer 102/202 may be a rectifier (for example, a rectified linear unit or ReLU). However, the present disclosure is not limited to this, and in some embodiments, all filter layers may be rectifiers, or only one filter layer may be rectifiers.

[0054] As described above, the denoising network 300 is between the VST network 100 and the IVST network 200. The denoising network 300 can be considered as a Gaussian denoiser. In some embodiments, the denoising network 300 may include (or may be) one or more stacked convolutional autoencoders (SCAE). According to an embodiment of the present disclosure, the autoencoder has a single hidden layer neural network architecture, which can be used to learn a meaningful representation of data in an unsupervised manner. The following describes a method of training SCAE according to an embodiment of the present disclosure.

[0055] Similar to the VST network 100 and the IVST network 200, the denoising network 300 may be a convolutional neural network (CNN) including multiple filter layers. For example, the denoising network 300 may include four filter layers 301-304. In some embodiments, each of the filter layers 301-304 may have a dimension of 3×3×1×10, and each of the first filter layer 301 and the second filter layer 302 may be a rectifier (eg, rectifier Linear unit or ReLU). However, the present disclosure is not limited to this, and in some embodiments, all filter layers 301-304 may be rectifiers.

[0056] The denoising network 300 may use a stacked convolutional autoencoder (SCAE) architecture. Any suitable number of SCAE filters (e.g., filter layers) in the denoising network 300 can be utilized. Auto encoder includes encoder and decoder.

[0057] The image denoising neural network training architecture may include a pure data neural network (for example, a bootstrap network). The pure data neural network can be used to train the denoising network 300 (for example, SCAE used to train the denoising network 300). The pure data neural network may also be a convolutional neural network (CNN), and may include the same number of filter layers (for example, the first filter layer to the fourth filter layer) 31-34 as the denoising network 300. The pure data neural network can be trained as SCAE more deeply by gradually adding encoder-decoder pairs. The encoder-decoder pair is trained to learn a sparse latent representation by using regularization to minimize the mean square error between the original pure image and the reconstructed image to achieve the sparseness of the latent representation. In some embodiments, the denoising network 300 and the pure data neural network may have the same architecture as each other. For example, in some embodiments, each of the filter layers 31-34 may have a dimension of 3×3×1×10, and only the first filter layer 31 and the second filter layer 32 may be rectifiers. However, the present disclosure is not limited to this, and the pure data neural network may have any number and/or arrangement of filter layers.

[0058] reference figure 1 with Figure 4 , The method of training image denoising neural network by using image denoising neural network training architecture (500) includes training variance stabilization transformation (VST) neural network 100 (s510), training inverse variance stabilization transformation (IVST) neural network 200 (s520) and/or train the denoising network 300 (s530).

[0059] In some embodiments, the VST network 100 and the IVST network 200 may be trained (eg, optimized) by using gradient-based stochastic optimization and/or block coordinate descent optimization. In some cases, gradient-based stochastic optimization can be used within block coordinate descent optimization. An example of gradient-based stochastic optimization is the Adam algorithm known to those skilled in the art

[0060] In some embodiments, the training of the VST network 100 (s510) and the training of the IVST network 200 (s520) may be performed jointly (or simultaneously). For example, the VST network 100 and the IVST network 200 can be trained together. In some embodiments of the present disclosure, a block coordinate descent optimization method is used, in which in each iteration, a parameter update is performed to reduce the VST network 100 target, and then a parameter update is performed to reduce the IVST network 200 target. In this way, the VST network 100 and the IVST network 200 are trained together (e.g., jointly or simultaneously trained).

[0061] The training of the denoising network 300 may include pre-training the denoising network 300, fine-tuning the denoising network 300, and guided training of the denoising network 300. The guided training of the denoising network 300 utilizes pure data neural networks (see, for example figure 1 ). As described further below, the pure data neural network acts as a proxy for the best denoising network.

[0062] In addition, information is shared between the pure data neural network and the denoising network 300 (see, for example figure 1 Dotted arrow in). The information sharing described further below regularizes the learning process of the denoising network 300. In addition, using the loss function described further below, this achieves joint sparsity between the pure data (eg, target data) input from the pure data neural network and the noise data input into the denoising network 300.

[0063] After training the image denoising neural network by, for example, the above-mentioned method, according to the embodiments of the present disclosure, the image denoising neural network can be used to improve images taken under weak lighting conditions. Figure 5 It shows a method of improving an image taken under a weak lighting condition by using a trained image denoising neural network according to an embodiment of the present disclosure.

[0064] As mentioned above, images captured under relatively weak lighting conditions usually have two image noise components-signal-related Poisson noise components and signal-independent Gaussian noise components.

[0065] The image (for example, damaged image or noisy image) input to the trained image denoising neural network is first operated by the VST network 100 (s610). The VST network 100 changes (for example, transforms or encodes) the input image to have a constant variance instead of depending on the variance of the input signal (for example, the input signal of the camera sensor). The VST network 100 is optimized to minimize the loss function that achieves a constant output variance, while ensuring monotonicity, to achieve the reversibility of the learned transformation under the conditional expectation for the pixel value. The resulting image signal is corrupted by noise with constant variance, and therefore can be modeled as Gaussian noise. That is, the trained VST network 100 is used to transform Poisson noise in the input image into Gaussian noise.

[0066] Next, the image (for example, an encoded image) is operated by the denoising network 300 (s620). The trained denoising network 300 removes Gaussian noise (or reduces the amount of Gaussian noise) in the image. For example, the image is passed through a continuous auto encoder to gradually reduce the amount of Gaussian noise present in the image. The trained denoising network 300 can be trained by minimizing the perceptual loss compared with a similarly transformed real noise-free image, or by minimizing the mean square error distance between the noise image and the noise-free image.

[0067] Next, the IVST network 200 operates the image (s630). The IVST network 200 acts as a decoder to return the image to its original domain, essentially reversing the encoding done by the VST network 100. The IVST network 200 is trained by minimizing the distance metric between the output from the identity transformation and the desired output of the cascade of the VST network 100 and the IVST network 200. For example, the IVST network 200 learns based on the identity mapping under the expected output, such as:

[0068] IVST(E[VST(y)|x])=x

[0069] Among them, y|x~Poi(x) and E(V) represent the expected value of V.

[0070] The above-mentioned features and/or steps of the embodiments of the present disclosure will be further described below.

[0071] Variance Stabilization Transformation (VST) Network 100 and Inverse Variance Stabilization Transformation (IVST) Network 200

[0072] When the image source x is recorded by a detector (for example, a digital camera sensor), a digital image (for example, a digital image signal) y is generated. Both x and y can be defined on a uniform spatial grid, where the (i, j)th generated image pixel y ij Depends only on x ij. Due to the quantum nature of light, given x ij In the case of y ij There is some uncertainty in it. The number of photons (i, j) recorded by the detector in T seconds then follows a rate of x ij Poisson distribution. This Poisson distribution can be modeled by Equation 1.

[0073] Equation 1:

[0074]

[0075] The Variance Stabilization Transformation (VST) smoothes the digital image, and should allow (for example, allow) accurate and unbiased inverse transformation under ideal circumstances. However, in some cases, VST may not allow accurate and unbiased inverse transformation. For example, when VST adopts Anscombe transformation, accurate and unbiased inverse transformation may not be allowed. This smoothing requirement of VSTΨ can be modeled by Equation 2.

[0076] Equation 2:

[0077] var(Ψ(y)|x)=1

[0078] An ideal denoiser (for example, an ideal Poisson denoiser) can be thought of as E[Φ(y)|x]. Next, recover x from E[Φ(y)|x] to provide the inverse VST. Then the inverse VST (IVST) and Π should satisfy Equation 3.

[0079] Equation 3:

[0080] ∏(E[Ψ(y)|x])=E[y|xl=x

[0081] However, according to some exemplary embodiments, not every VST will provide an IVST that satisfies Equation 3, and not every IVST will provide a VST that satisfies both smoothing and inverse transformation requirements.

[0082] According to an embodiment of the present disclosure, the VST network 100 and the IVST network 200 are provided by two neural networks. According to an embodiment of the present disclosure, the method of training the VST network 100 and the IVST network 200 is described as follows.

[0083] The neural networks of the VST network 100 and the IVST network 200 can each have a parameter θ VST And θ IVST. Generate training set Such that for each x n , From Poi(y nm , X n ) Randomly selected y nm. Assume Where Ψ NN (·) refers to the VST transformation implemented by the VST neural network 100, and Ψ NN (y nm ) Is in response to input y nm Shorthand for the output of the VST network 100. Without loss of generality, let x 1 2 N. Then, according to one embodiment, equation 4 is optimized to provide VST.

[0084] Equation 4:

[0085]

[0086] In Equation 4, n′=n-1 and with Respectively refers to calculating the empirical mean and variance of the input data set. The first term in the objective function follows the smoothing requirements, and the second term in the objective function is to ensure that the learned transformation is monotonic, so the reversibility condition is feasible. When Ω n When the empirical mean value of is a monotonically increasing function of n, the second term in the objective function is equal to 0, and it is guaranteed that there is an IVST that meets the reversibility condition.

[0087] For example, learn IVST by optimizing Equation 5 that follows the reversibility condition.

[0088] Equation 5:

[0089]

[0090] In some embodiments of the present disclosure, a block coordinate down training method is used to train the VST network 100 and the IVST network 200, wherein in each iteration, a parameter update is performed to reduce the VST target, and then a parameter update is performed to reduce the IVST target. Therefore, training (for example, jointly or simultaneously training) the VST network 100 and the IVST network 200 together ensures that there is a corresponding and accurate IVST for the trained VST.

[0091] Denoising network 300

[0092] Refer to above figure 1 As described, the denoising network 300 may include (or may be) one or more stacked convolutional autoencoders (SCAE). The following describes a method of training SCAE as the denoising network 300 according to an embodiment of the present disclosure.

[0093] Consider an example where the denoising network 300 includes K convolutional autoencoders. In response to the input y, the output of the denoising network 300 is given by Equation 6.

[0094] Equation 6:

[0095]

[0096] In Equation 6, with Respectively represent the encoding and decoding functions of the k'th convolutional autoencoder. function And function These are given by Equation 7 and Equation 8, respectively.

[0097] Equation 7:

[0098]

[0099] Equation 8:

[0100]

[0101] In Equation 7 and Equation 8, R represents the number of filters in the encoder and decoder, and φ(·) is a scalar nonlinear function applied to each element of the input. Here, φ(·) is set as a rectified linear function.

[0102] According to some embodiments, the denoising network 300 can be further trained in two steps: 1) a pre-training (or baseline training) step; 2) a fine-tuning step.

[0103] Denoising network 300 pre-training

[0104] reference figure 2 According to an embodiment of the present disclosure, the pre-training step occurs after the training of the VST network 100 and the IVST network 200. The pre-training of the denoising network (for example, denoising SCAE) 300 includes a sequence of K steps.

[0105] The denoising network 300 is presented with noisy input (or noisy data) Where y is the target data, and the purpose is to restore y. The input of the denoising network 300 in the objective function can be replaced by To learn network parameters. in figure 2 , The encoder (for example, the VST network 100) and the decoder (for example, the IVST network 200) are respectively referred to as with And will The potential representation of is referred to as among them The VST network 100 and the IVST network 200 can be regarded as the first encoder/decoder pair.

[0106] Such as figure 2 As shown, the denoising SCAE 300 is arranged between the trained VST network 100 and the trained IVST network 200. Consider the k′th encoder/decoder pair arranged between the (k-1)′th encoder/decoder pair (for example, the VST/IVST network pair 100/200), and the k′th encoder/ The decoder pair is greedily optimized, while other layers (for example, other encoder/decoder pairs) are frozen by using a loss function, as shown in Equation 9.

[0107] Equation 9:

[0108]

[0109] In Equation 9, θ k Indicates the weight and deviation of parameterizing the k'th denoising SCAE 300.

[0110] In some embodiments, a stacked sparse denoising autoencoder (SSDA) can be used instead of a single-layer sparse denoising autoencoder.

[0111] Fine tuning of denoising network 300

[0112] In some embodiments, the fine-tuning of the denoising network 300 includes end-to-end fine-tuning by optimizing Equation 10.

[0113] Equation 10:

[0114]

[0115] Guided learning

[0116] As mentioned above, according to some exemplary embodiments, SCAE (such as SCAE for pure data neural networks for learning potential representations of input signals) has a neural network architecture, which can be used to learn meaningful data in an unsupervised manner. Said. For example, automatic encoders include encoder g: R d →R m And decoder f: R m →R d. The encoder maps the input y to the latent representation h given by Equation 11, and the decoder maps h to Equation 12.

[0117] Equation 11:

[0118] h=g(y)=φ(W e y+b e )

[0119] Equation 12:

[0120] f(h)=ψ(W d h+b d )

[0121] In Equation 11 and Equation 12, φ(·) and ψ(·) are nonlinear scalar functions for each element of the input vector. The purpose is to make f(g(y))≈y, so that after the pure signal y is encoded using the encoder g(y), the pure signal y is reconstructed using the decoder f(h) in order to learn the latent representation h, and The network parameters can be learned by solving Equation 13.

[0122] Equation 13:

[0123]

[0124] In Equation 13, θ={W e , B e , W d , B d }, N represents the number of training points, and y i Indicates the i'th training point.

[0125] However, autoencoders do not necessarily learn meaningful representations of data, where the term "meaningful" is contextual. In order to manipulate the autoencoder, additional constraints are added to the structure or objective function of the autoencoder, thereby manipulating the autoencoder to learn potential representations with certain attributes.

[0126] For example, if h (of Equation 11 and Equation 12 above) is constrained to be under-complete, meaning m d. In this case, the auto-encoder objective function is modified so that the auto-encoder learns a sparse latent representation. An autoencoder that learns sparse latent representations can be called a "sparse autoencoder". To this end, the objective function can be modified to Equation 14.

[0127] Equation 14:

[0128]

[0129] When H=[h^1… h N ], equations 15 and 16 are as follows.

[0130] Equation 15:

[0131]

[0132] Equation 16:

[0133]

[0134] In Equation 15 and Equation 16, h i [j] is h i The j′th element of τ is a scalar. When τ is assigned a small value, the sparsity is improved. Additional regularization means having a mean value τ and a mean value ρ averaged over all j j Kullback-Leibler divergence (KLD) between Bernoulli random variables.

[0135] Sparse autoencoder is a useful architecture for denoising, in this case it is called "sparse denoising autoencoder". In this case, the input signal is a noise signal Denoising encoder Encoding and then denoising decoder Decode to remove the noise signal Construct pure signal y i , And the encoder-decoder pair can be trained by minimizing the distance metric as in Equation 16b below. Equation 16b:

[0136]

[0137] In some embodiments, its input and target output can be changed by adding (for example, stacking) with The additional denoising autoencoder is shown to make the denoising network 300 deeper. The number of denoising autoencoders is not limited, and additional denoising autoencoders can be added to provide a deeper structure. In some embodiments, the SSDA parameters are learned in a greedy manner by optimizing the denoising autoencoder target for one sparse denoising autoencoder at a time. Then a stacked sparse denoising autoencoder (SSDA) structure is used to initialize the deep neural network (DNN) denoiser, which is fine-tuned by optimizing Equation 17.

[0138] Equation 17:

[0139]

[0140] In Equation 17, Indicates response to input The output of the denoising network 300, and Represents the collection of all parameters of the DNN.

[0141] In some embodiments, SSDA is trained. One challenge of learning a single sparse denoising autoencoder is to find a good encoder At a high level, the encoder definition is assigned to The potential representation of, and the quality of the representation can define the optimal denoising performance of the autoencoder. In some embodiments, the encoder g(·) of an autoencoder trained on pure data (e.g., relatively noise-free images) (e.g., a pure data neural network) is used as a proxy for the best denoising encoder And used to pass The distance between and g(·) will be used to train the regularization of the objective function of each denoising autoencoder. g(·) and The distance between can be measured by h and Quantify the joint sparsity between.

[0142] A sparse denoising autoencoder (SDA) (for example, a single SDA) can be jointly trained with pure SCAE by modifying the objective function to include constraints on both pure SCAE and noisy SCAE and realize their learning as in Equation 18. The joint sparsity of the latent representation of.

[0143] Equation 18:

[0144]

[0145] In Equation 18, Defined by Equation 19.

[0146] Equation 19:

[0147]

[0148] In Equation 18 (for example, the objective function), the first and second terms correspond to the sparse autoencoder (for example, SDA) reconstruction loss of the pure data neural network, and the third and fourth terms correspond to the sparse automatic Encoder denoising loss, and the last term indicates that g(·) is linked to The guiding term of, which regularizes learning by maximizing the joint sparsity between the latent representation learned by the pure data neural network and the latent representation learned by the denoising network. Joint sparsity regularization attempts to improve h with similar sparsity contours i with

[0149] In some embodiments, the guided SSDA (G-SSDA) objective function is differentiable and can be optimized using, for example, stochastic gradient-based optimization techniques.

[0150] The embodiments of the present disclosure provide a flexible method for training the denoising network 300, which can be incorporated into a variety of different denoising architectures (for example, denoising neural networks), and can be modified so as to reconstruct The error term is replaced by the classification error term. By replacing the reconstruction error term with the classification error term, the denoising neural network can be used for image classification and organization instead.

[0151] Initially, the guided autoencoder (for example, image denoising neural network) will be relatively far away from the target image (for example, a pure image or a noise-free image). Therefore, in the early stages of training, λ 3 (See, for example, Equation 18) may not be used as a reference. However, as the training progressed, the guided autoencoder was improved, proving that the larger regularization parameters are reasonable. Therefore, in some embodiments, λ 3 Increase at a log-linear rate.

[0152] The guided SDA training method according to an embodiment of the present disclosure can be extended to a deeper structure (for example, a deeper network). In other embodiments, a guided autoencoder (for example, a pure data network) can be used as an alternative training strategy for the guided SDA training method.

[0153] image 3 An example of training a denoising network with an SSDA architecture including two SDA 410/420 is shown. The first of the two SDAs (for example, the trained SDA or pure data autoencoder) 410 has been pre-trained, and the second 420 of the two SDAs has not started training. SDA 410/420 can refer to the pure data neural network and the denoising network 300 respectively. For example, the trained SDA 410 has been trained by using pure data (e.g., on pure or relatively noise-free images) and can be considered as the best SDA agent.

[0154] The baseline strategy for training the second SDA (for example, untrained SDA or noisy data autoencoder) 420 is to optimize equation 20, where, It is the new encoder and decoder functions to be learned in SDA.

[0155] Equation 20:

[0156]

[0157] However, according to an embodiment of the present disclosure, the network uses g 1 (y) As the target data of the second SDA 420, not used As the target data of the second SDA 420, g 1 (y) is the coding output of the pure data neural network at the corresponding network level. Therefore, the objective function represented by Equation 21 can be optimized.

[0158] Equation 21:

[0159]

[0160] Instead of the latent representation assigned to y by the second SDA 420, SSDA uses the latent representation assigned to y by the first SDA 410 as the target data, because Instead of learning by using noisy input (e.g., noisy input signal), g(·) is learned by using pure input (e.g., pure input signal), so it should provide a better potential representation of the target.

[0161] Next, by minimizing (or optimizing) The distance between g(·) and the objective function (for example, Equation 21) is regularized to train the second SDA 420. For example, by measuring the latent representation h of dimension m and Joint sparsity between And g(·) such that H=[h 1 … H N ].

[0162] Next, the loss function represented by Equation 22 is optimized.

[0163] Equation 22:

[0164]

[0165] The optimization of the loss function (eg, equations 19 and 22) provides joint training of the pure data autoencoder 410 and the noisy data autoencoder 420.

[0166] When the pure data autoencoder 410 is pre-trained, its potential representation can be used as the target of each additional autoencoder (for example, each additional encoder/decoder pair) of the pre-trained noisy data autoencoder 420.

[0167] Refer to above Figure 5 As mentioned, once the image denoising neural network has been properly trained by the methods described herein, it can be used to denoise any appropriate input image. For example, users can take digital images by using a mobile phone camera. When an image is taken under relatively weak lighting conditions, it may be affected by relatively high noise and result in low-quality images. In order to remove or reduce the noise in the image, the image can be input to the image denoising neural network. The image denoising neural network can run on the processor of a mobile phone, for example, and can run automatically when the image is taken. Then, the VST network 100 transforms (or encodes) the image so that it has a constant or substantially constant output variance. Next, the denoising network 300 will remove or reduce the Gaussian noise present in the image. Finally, the IVST network 200 transforms (or decodes) the image back into its original domain. Therefore, the user is provided with an output image that has less noise than the input image and thus has a higher quality.

[0168] Although the present disclosure has been described with reference to exemplary embodiments, those skilled in the art will recognize that various changes and modifications can be made to the described embodiments, all without departing from the spirit and scope of the present disclosure. In addition, those skilled in various fields will recognize that the present disclosure described herein will suggest solutions for other tasks and adaptability for other applications. The applicant’s intention is to cover all these uses of the present disclosure and those changes and modifications that can be made to the exemplary embodiments of the present disclosure selected herein for disclosure by the claims herein, all without departing from the present disclosure Spirit and scope. Therefore, the exemplary embodiments of the present disclosure should be regarded as illustrative rather than restrictive in all aspects, and the spirit and scope of the present disclosure are indicated by the appended claims and their equivalents.