[0043] The embodiments of the present invention will be described in further detail below with reference to the accompanying drawings.
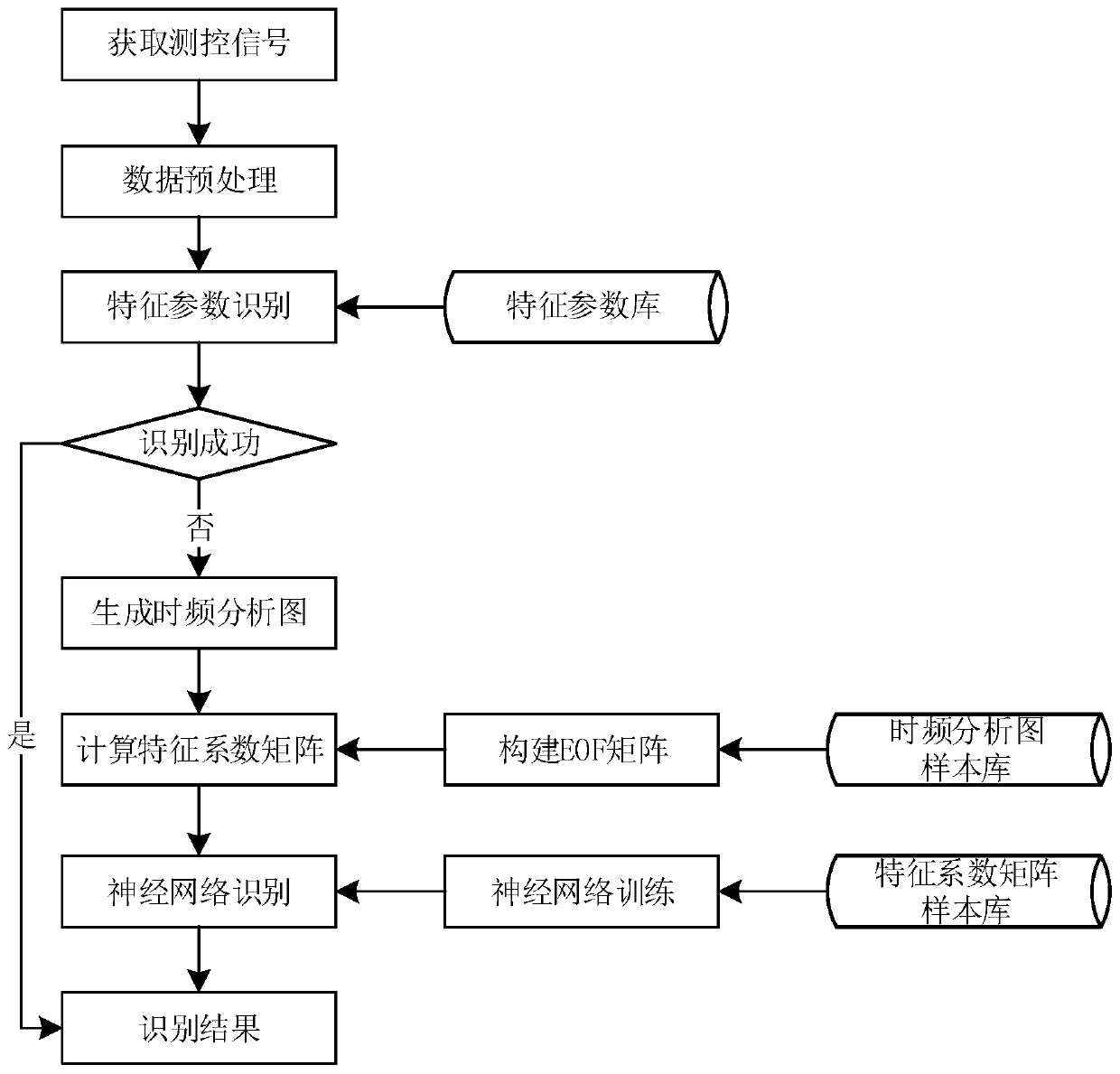
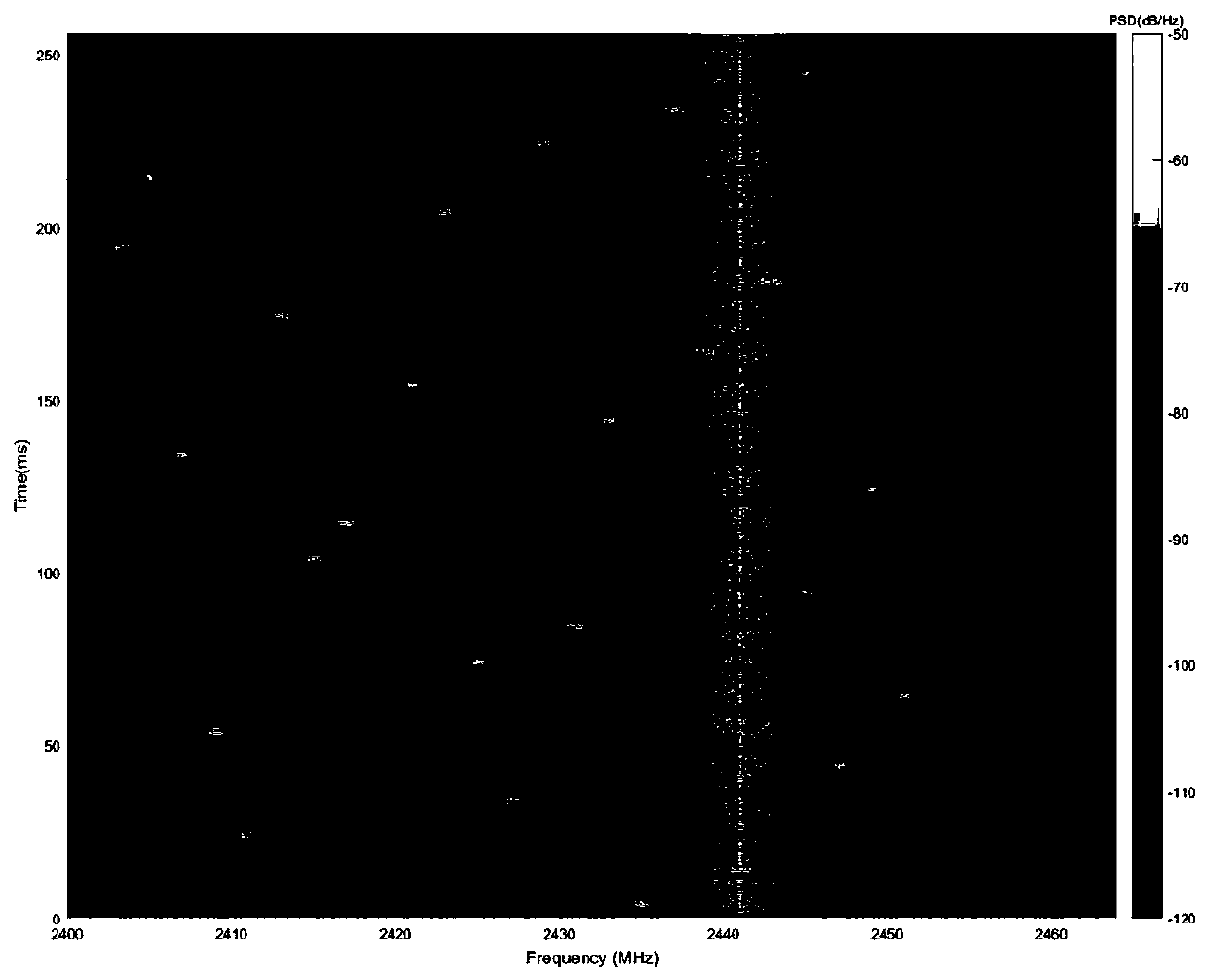
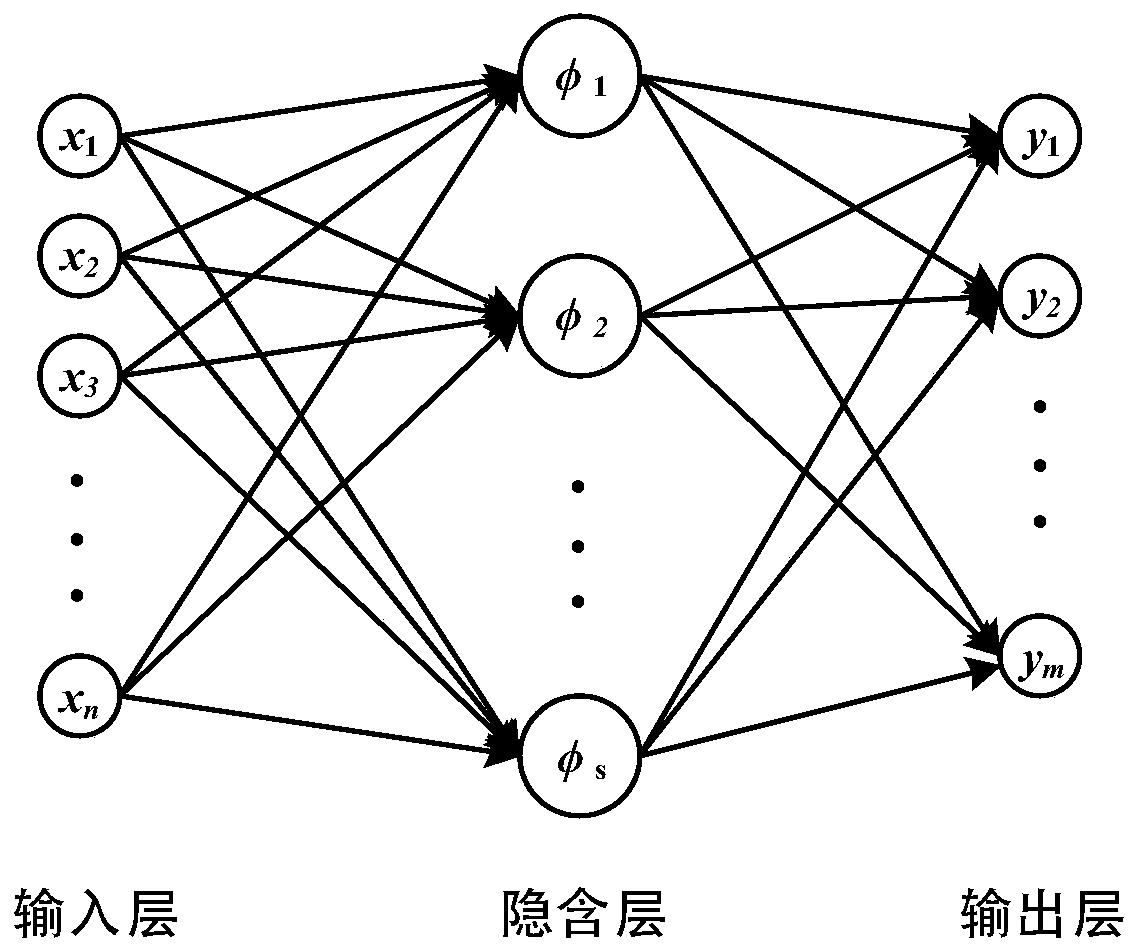
[0044] Aiming at the problem that similar UAV signals are difficult to identify, the present invention proposes an EOF-based UAV signal identification method. The specific principle of EOF is as follows.
[0045] Empirical Orthogonal Function (EOF) is an analysis method that separates the contributions of different physical processes and mechanisms to the variable field through the analysis of observation data. The basic idea of the EOF method is to think that a large amount of related data must always have common factors that dominate. Under the condition of not losing or losing the information contained in the original data as much as possible, the original data is simplified to extract the characteristic information of the original data. Using the EOF method, we can identify the main orthogonal spatial distribution patterns from the data set of the variable field and extract the main independent new variable sequences from the multivariate sequence, so as to use a few new variable sequences to reflect the original multiple variables Change information. Using this method can help us grasp the main points more easily when studying problems with more complicated mechanisms.
[0046] When we analyze observations or model data, in principle, we should treat them as random variables, because they contain the influence of many contingency factors. Consider an m-dimensional random vector X composed of variables on m grid points in time or space. For convenience, it is assumed that the mathematical expectation of the original variable has been removed, that is, X is an anomaly field, and its expectation value E(X)=0. Now select the sample X with the capacity n of X 1 , X 2 ,..., X n , Each sample is an m-dimensional column vector:
[0047] X t =(x 1t ,x 2t ,L,x mt ) T t=1,2,L,m (3)
[0048] Now, we need to find a set of orthogonal basis vectors, we can put X t Express it as accurately as possible. The linear combination of such a set of orthogonal basis vectors can be expressed as:
[0049]
[0050] Where V u Is the u-th vector among the m orthogonal basis vectors. There are N vectors in this group, N u (t) is for the t-th sample X t Vector V u The corresponding weight coefficient. ε t Represents the error vector.
[0051] In order to determine the orthogonal basis vector group for sample X t For the expression effect of, we define the sample average of the residual error sum of squares:
[0052]
[0053] The smaller E is, the higher the degree of agreement between the result of orthogonal basis vector fitting and X is.
[0054] V 1 , V 2 ,..., Vu is established in sequence. First we consider the basis vector V 1 The corresponding expansion is:
[0055] X t =a 1 (t)V 1 +ε t t=1,2,L,m (6)
[0056] Our goal is to make E 1 Reach the minimum.
[0057] From formula (2), formula (3) can be obtained,
[0058]
[0059] considering Have
[0060]
[0061] And V is the normalized vector, Therefore, formula (5) can be reduced to
[0062]
[0063] Where VarX is the total variance of field X, which is the same as V 1 And a 1 (t) Irrelevant. P is the covariance matrix of X.
[0064]
[0065] E 1 Is V 1 The function of v 11 , V 21 ,...V m1 Is a multivariate function of the independent variable, so that it is in V 1 T V 1 The minimum value is reached when =1. This is a conditional extreme value problem of a multivariate function, which can be solved by the Lagrangian conditional extreme value method.
[0066] Construct auxiliary function:
[0067]
[0068] To get the extreme value, equation (7) is required for V 1 The partial derivative of is 0, that is
[0069]
[0070] Therefore:
[0071] PV 1 =λ 1 V 1 (13)
[0072] Visible V 1 Is the eigenvector of the covariance matrix P, and the corresponding eigenvalue is λ. At this time E1 reaches the minimum,
[0073] E 1 =VarX-λ 1 (14)
[0074] By analogy, the u-th orthogonal basis vector V u Satisfy:
[0075] PV u =λ u V u u=1,2,L m (15)
[0076] Consider the linear combination of the first N orthogonal basis vectors,
[0077]
[0078] It can be seen that all V u In fact, they are all determined by the self-correlation structure of the analyzed field X. These V u The set of is the empirical orthogonal function.
[0079] Considering that P is a real symmetric matrix, by the eigenvalue properties of the real symmetric matrix, there is
[0080]
[0081] Therefore, if N=m, that is, complete expansion of order m, then
[0082]
[0083] Definition due to V u The addition of to reduce the error E by V u The variance contribution of Q u ,Have:
[0084]
[0085] From this, V u The variance contribution rate of is:
[0086]
[0087] The cumulative variance contribution rate of the first N eigenvectors is:
[0088]
[0089] Consider the matrix M,
[0090]
[0091] Each row of the matrix M is a sequence of values of data on the same grid point in different samples, and each column is a sequence of data on the same sample at each grid point.
[0092] A matrix can be formed by using the first N eigenvectors as column vectors:
[0093]
[0094] Each column of the matrix is an eigenvector.
[0095] The weight coefficients corresponding to the first N eigenvectors form a matrix a,
[0096]
[0097] The matrix is a sequence of weight coefficients corresponding to different eigenvectors of the same sample along the column direction, and the matrix is the weight coefficients of the same eigenvector corresponding to different samples along the row direction.
[0098] The matrix ε is formed by the residual error
[0099]
[0100] The relationship can be expressed as:
[0101] M=Va+ε (26)
[0102] For the entire sample set M, we can use the empirical orthogonal function V and the characteristic coefficient matrix a to fit, and the effect of the fitting can be seen from the deviation matrix ε. Where a is the characteristic coefficient matrix used for identification.
[0103] When analyzing data with obvious regularity such as time-frequency analysis graphs, the empirical orthogonal functions obtained from the sample data, if arranged according to the eigenvalues corresponding to the eigenvectors, often the first few eigenvectors (set to N) correspond to The variance contribution rate is much larger than other eigenvalues, that is to say, the first N items occupy a very large proportion in the fitting. Tests have proved that for the time-frequency analysis graph obtained by FFT with 1024 points, if N=10, the cumulative variance contribution rate of these feature vectors can reach 90%, and if N=100, the cumulative variance contribution rate can reach More than 99% is close to 100%. In this case, the linear combination of the first N feature vectors can be used to fit the data distribution, thereby simplifying the difficulty of data analysis and processing. In this way, the structure that may have required tens of thousands of parameters to determine can be characterized by a small number of weight coefficients through the determined empirical orthogonal function, which can effectively reduce the amount of calculation. At the same time, the number of feature parameters used for identification is greatly reduced. Effectively improve the stability of recognition.
[0104] Such as figure 1 Shown is a flow chart of the EOF-based UAV signal recognition method of the present invention.
[0105] An EOF-based UAV signal recognition method, including the following steps:
[0106] 1) First, the received UAV signal is initially identified by the method of feature parameter matching;
[0107] 2) For UAV signals that cannot be identified through feature parameter matching, after performing FFT processing, the corresponding time-frequency analysis diagram is generated;
[0108] 3) Using the empirical orthogonal function analysis method, the video analysis matrix corresponding to the video analysis diagram is decomposed into the EOF matrix reflecting the common characteristics of the signal and the characteristic coefficient matrix reflecting the signal difference characteristics;
[0109] 4) Perform feature data extraction and BP neural network training on the feature coefficient matrix, construct the corresponding UAV type classifier, and output the recognition results.
[0110] After we obtain the signal, we first perform data preprocessing, and then perform feature parameter extraction, and use the extracted feature parameters to match the data in the feature parameter library. For drones with large signal differences, the identification can be completed after parameter matching; including Calculate the key parameters of the signal's center frequency, bandwidth, and frequency hopping signal time slot, and compare them with the corresponding data in the characteristic parameter library.
[0111] If the matching recognition fails, a time-frequency analysis graph is generated for the next step of recognition. Such as figure 2 As shown, the time-frequency analysis diagram uses the observation data of a period of observation time for sampling, and intercepts a period of sampled data every time difference △t for FFT processing. The obtained spectrum data is used as a column of data, and these data are arranged in chronological order. Construct a time-frequency analysis matrix and generate a time-frequency analysis graph, figure 2 The abscissa is the frequency and the ordinate is the time. The gray scale of each point represents the spectral coefficient at the corresponding time and frequency. Then we use a large number of video analysis graph sample libraries of similar-signal drones accumulated by experiments and data collection to construct the corresponding EOF matrix and the feature coefficient matrix library corresponding to different drones. The EOF matrix is used to time the current target. Frequency analysis graph is used to calculate the characteristic coefficient matrix. The characteristic coefficient matrix sample library is used for neural network training. Finally, we use the calculated characteristic coefficient matrix as input for recognition and output the recognition result.
[0112] The EOF matrix is required to be solved, and a sample library of time-frequency analysis graphs is required. These samples are mainly from the collection of time-frequency analysis graphs generated by the measured data of drones with similar signals. Arranging these according to a certain rule, an m×n sample matrix can be constructed, which can be expressed as:
[0113]
[0114] Then calculate its anomaly matrix:
[0115]
[0116] Where △xij represents the anomaly value:
[0117]
[0118] From this, the covariance matrix of B can be obtained:
[0119]
[0120] among them
[0121] From the above formula
[0122]
[0123] Use Jacobian orthogonal transformation to transform it into a diagonal square matrix with all other elements being 0:
[0124]
[0125] Introduce orthogonal matrix:
[0126]
[0127] Use orthogonal matrix to perform orthogonal transformation:
[0128] P (1) =(Φ (1) ) T P (0) Φ (1) (34)
[0129] And so on:
[0130]
[0131] Continuous conversion in this way can make P (s) Gradually approach ∧.
[0132] P (s) =V T P (0) V→Λ (36)
[0133] Where V is the product of all orthogonal matrices, that is, the EOF matrix:
[0134]
[0135] Where V i Is the eigenvector, which corresponds to the element λ of ∧. Generally, the value of λ is used as the measurement standard to determine how many order eigenvectors should be used to form the EOF matrix. How many order eigenvectors need to be taken for fitting, and the cumulative variance contribution rate of these eigenvectors needs to be considered, which can be expressed as:
[0136]
[0137] Where λi represents the characteristic value corresponding to Vi. The size of Hu directly reflects the fitting degree of the original Nu orthogonal basis vectors to the original variables. Due to the characteristics of the empirical orthogonal function itself, when analyzing some structures with strong regularity, the cumulative variance contribution rate of the orthogonal basis vector with the largest contribution rate in the front part of the EOF matrix can be very high. In this case, you can The linear combination of these eigenvectors is used to fit the original data distribution. Generally speaking, if the variance contribution rate of the first N-order eigenvectors reaches more than 90%, we can only use the first N-order eigenvectors to construct the EOF matrix, thus Simplify the difficulty of data analysis and processing. In order to ensure the completeness of the data as much as possible, the order of the eigenvectors with a variance contribution rate of more than 99% can also be selected. Generally, for the time-frequency analysis graph obtained by FFT with 1024 points, the first 100 orders can be used completely. fulfil requirements.
[0138] Let's introduce the method of orthogonal conversion in detail below.
[0139] Consider the sth round of orthogonal transformation process:
[0140] P (S) =(Φ (S) ) T P (S-1) Φ (S). (39)
[0141] Where P (s-1) Is the matrix before the sth round of conversion. P (s) Is the matrix after the sth round of conversion, Φ (s) Is the S round conversion matrix.
[0142]
[0143]
[0144] The result of the operation can be summarized as:
[0145]
[0146] After each round of conversion, the elements of the corresponding orthogonal matrix V will also change:
[0147]
[0148] Using orthogonal transformation, the purpose is to make all the elements of the non-main diagonal tend to 0, so in each transformation, you must use:
[0149]
[0150] Incorporating formula (38), you can get:
[0151]
[0152] Where σ and μ are the intermediate parameters taken by the simplified expression,
[0153]
[0154] Therefore:
[0155]
[0156] Where w is the intermediate parameter taken by the simplified expression, and its value is:
[0157]
[0158] In this way, the orthogonal transformation is used repeatedly, and the diagonal matrix ∧ can be obtained.
[0159] But in actual calculations, a critical value ε can be selected so that the absolute value of each off-diagonal element is less than this value:
[0160]
[0161] When all the non-diagonal elements satisfy the above formula, we can consider that the non-diagonal elements are sufficiently small.
[0162] The calculation of the characteristic coefficient matrix requires the EOF matrix V and the time-frequency analysis matrix D. The time-frequency analysis matrix D is the matrix corresponding to the time-frequency analysis diagram obtained after data processing of the target signal in a period of time. Each row of the matrix represents different Frequency, each column represents a different time, the time-frequency analysis matrix D can be expressed as follows:
[0163]
[0164] Where m represents the number of samples of the time-frequency analysis matrix FFT, and n is the number of time points at which data is collected at intervals of Δt within a period of time.
[0165] If we select the number of feature vectors as N, the EOF matrix V can be expressed as:
[0166]
[0167] The characteristic coefficient matrix a can be expressed as:
[0168]
[0169] When the selected eigenvectors are large enough and the cumulative variance contribution rate is large enough, we can think that as long as the target exists in the sample library, the deviation matrix ε is negligible. Therefore, the relationship between the characteristic coefficient matrix a and D, V can be expressed as:
[0170] D=Va (50)
[0171] Therefore, the coefficient matrix a can be expressed as:
[0172] a=V -1 D (51)
[0173] In the actual operation, the calculation of matrix inversion is large and unnecessary errors are easily introduced. Therefore, iterative algorithm can be used to solve the characteristic coefficient matrix. Here we can use the ART iterative algorithm to solve the problem. The iterative equation is as follows:
[0174]
[0175] Where the superscript (k) represents the initial value a (0) The result of the k-th iteration. λ k For the relaxation factor, the value is between 0 and 2. For data containing measurement errors, a proper selection of the relaxation factor can improve the quality of the reconstructed image and the efficiency of iteration. Generally, the relaxation factor can take a fixed value during the iteration process.
[0176] Finally, based on the neural network image classification algorithm, combined with UAV signal characteristics, an automatic signal recognition method is realized. The specific method is as follows:
[0177] 1) Feature data extraction
[0178] This paper adopts HOG+LBP hybrid feature extraction method to extract the feature data of the time-frequency analysis graph.
[0179] HOG feature is a descriptor that describes local information. The edge information is expressed by calculating the gradient histogram of the area pixels, and then normalized to improve the performance of the feature. The normalization operation on local cell units can enhance the robustness of HOG features to image geometric transformation. The most distinctive advantage of the HOG feature lies in the histogram statistics divided by blocks, and it has good anti-interference ability to the changes of light and background. In the time-frequency analysis graph, for the uneven distribution of color noise and the appearance of broadband The edge information of the target signal can still be extracted under fixed frequency interference.
[0180] The HOG feature extraction steps are:
[0181] 1. Read in the picture, and standardize the picture Gamma space and color space. In order to reduce the interference of light changes, local shadows and other factors, so that the image has the same standard, it can also have a certain suppression effect on noise interference. The amplitude of the signal time and frequency points can be converted into a single-channel grayscale waterfall map, and the pixel gray The degree range is [0, 255], and the gamma compression formula is:
[0182] I(x,y)=I(x,y) gounma (53)
[0183] 2. Calculate the gradient of the gray value of each pixel in the graph and save it as a table. The gradient calculation formula is as follows:
[0184]
[0185] 3. Determine the scanning parameters of the sliding window, such as the length and width of the window, the window moving step, and use the coordinate origin (upper left corner of the image) as the current position of the sliding window.
[0186] 4. Intercept the area in the picture where the sliding window is located as a block. Divide the block into four equal parts, and calculate the gradient of the pixel points in each cell according to the gradient direction: divide the gradient direction in each cell into 9 equal bins, and the 9 bins correspond to each component of the 9-dimensional vector . Then traverse the pixels in the cell in turn, and count the gradient direction. If the direction falls within the range of that bin, the value of the component corresponding to the vector increases by 1. Use this method to count the vectors corresponding to all cells.
[0187] 5. Normalize the histogram of each small block, which can have better invariance to lighting, shadows, edge contrast, etc.
[0188] 6. Move the sliding window according to the specified step and go to step 4. If the sliding window cannot be moved, that is, the last piece of the picture has been reached, go to step 7.
[0189] 7. Concatenate the feature vectors of all small blocks to form HOG feature data
[0190] The LBP feature (Local Binary Pattern, LBP) is often used in the field of machine vision to describe the local texture features of an image. The basic idea is to compare the gray value of each pixel with the gray value of the neighboring pixels as a threshold. If it is greater than the threshold, it is recorded as 1, otherwise it is recorded as 0, and the result is saved as a binary number. Describe the local texture features of the image. The LBP algorithm does not use a single pixel to describe the texture, but uses a local area pattern to describe the texture, and links the value of each pixel to the description code value of the local texture. It is a local feature algorithm; at the same time, The LBP algorithm also has the characteristics of statistical features. It counts the number of different modes in the entire image. The LBP feature has both statistical and structural features. Therefore, the LBP method has more advantages than other texture algorithms, and has a wide range of applications in texture classification and recognition.
[0191] The LBP feature extraction steps are:
[0192] 1. Divide the detection window into 16×16 cells;
[0193] 2. For a pixel in each cell, compare the gray values of the adjacent 8 pixels with it. If the surrounding pixel value is greater than the central pixel value, the position of the pixel is marked as 1, otherwise it is 0. In this way, 8 points in the 3*3 neighborhood can be compared to generate an 8-bit binary number, that is, the LBP value of the center pixel of the window can be obtained;
[0194] 3. Then calculate the histogram of each cell, that is, the frequency of appearance of each number (assumed to be a decimal number LBP value); then normalize the histogram.
[0195] 4. Finally, connect the obtained statistical histogram of each cell into a feature vector, which is the LBP texture feature vector of the entire image;
[0196] Although a single feature has a smaller feature dimension than a hybrid feature, its accuracy is often not as good as a hybrid feature that is described from multiple angles. Therefore, this paper adopts hybrid features based on multi-feature fusion. Although the dimensionality of the mixed feature is greater than that of a single feature, which leads to a decrease in the speed of the feature extraction process. Feature extraction takes a longer time in the offline training phase, but it can improve the recognition ability of the classifier.
[0197] After the sample HOG feature extraction and LBP feature extraction are completed, the two features need to be fused to obtain mixed features. At present, feature fusion mainly includes feature combination, feature selection, and feature transformation. This paper uses the serial method in feature combination to complete the fusion of HOG features and LBP features, mainly considering: in the actual processing process, it is found that HOG features and LBP features have similar eigenvalue ranges in each dimension, so you can directly use serial The way to achieve feature fusion, and the fused features do not need to be normalized.
[0198] 2) Neural network training
[0199] This paper takes the feature data samples obtained by HOG+LBP hybrid feature extraction as input, and uses neural network training to realize the recognition function of video analysis graphs. In training, the RBF neural network is mainly used, which is an improved method of BP neural network, which can effectively improve the problem of BP neural network easily falling into local minimum. This paper adopts the Gaussian radial basis kernel function, and its expression is:
[0200]
[0201] Where K(x,c i ) Is the kernel function, x is the training sample, c i Is the center vector of each basis function, and σ is the width of the kernel function.
[0202] RBF neural network structure diagram such as image 3 As shown, the network is a three-layer static forward network, which is divided into three layers: input layer, hidden layer and output layer. The first layer is the input layer, which is composed of the feature data samples obtained from the above-mentioned mixed feature extraction. The second layer is the hidden layer. The mapping from the input layer space to the hidden layer space is nonlinear, and the third layer is the output layer. The output is the judgment probability of various types of drones. The mapping from the hidden layer space to the output layer space is linear, and the weight coefficient w here is an adjustable parameter. We can collect those similar UAV signals, generate time-frequency analysis graphs, calculate through feature coefficient matrix and extract feature parameters, and obtain data samples as input samples of neural network for training, and then we can build the classifier of the corresponding UAV type . After the actual measurement of the UAV time-frequency analysis chart is obtained, the UAV type can be identified in real time.
[0203] Correspondingly, an EOF-based UAV signal recognition system includes a characteristic parameter recognition module, a time-frequency analysis graph generation module, an EOF analysis module, a characteristic extraction and classification recognition module; the characteristic parameter recognition module is used for matching through characteristic parameters The method performs preliminary identification of the received UAV signal; the time-frequency analysis graph generation module is used to perform FFT processing on the UAV signal that cannot be identified through feature parameter matching, and then generates the corresponding time-frequency analysis graph; EOF analysis module Used to use the empirical orthogonal function analysis method to decompose the video analysis matrix corresponding to the video analysis graph into the EOF matrix reflecting the common characteristics of the signal and the characteristic coefficient matrix reflecting the signal difference characteristics; the feature extraction and classification recognition module is used to analyze the characteristic coefficient matrix Perform feature data extraction and BP neural network training, build a corresponding UAV type classifier, and output the recognition results.
[0204] Among them, the EOF analysis module includes a time-frequency analysis graph sample library, an EOF matrix construction unit and a characteristic coefficient matrix calculation unit; the EOF matrix construction unit uses the video analysis graph sample library to construct the corresponding EOF matrix, and the characteristic coefficient matrix calculation unit uses the EOF matrix Calculate the characteristic coefficient matrix with the time-frequency analysis matrix. The feature extraction and classification recognition module includes a feature coefficient matrix sample library, a feature data extraction unit, and a classification recognition unit; the feature data extraction unit uses the feature coefficient matrix sample library to extract HOG features and extract LBP features, and use the feature combination in The serial method completes the fusion of HOG features and LBP features. The classification and recognition unit is used to train the neural network, construct a corresponding UAV type classifier, and output the recognition result. The characteristic parameter recognition module includes a characteristic parameter library, including characteristic parameters for preliminary recognition of UAV signals.
[0205] It should be pointed out that the specific implementations described above may enable those skilled in the art to understand the invention and creation more comprehensively, but do not limit the invention and creation in any way. All technical solutions and improvements that do not depart from the spirit and scope of the invention are covered by the protection scope of the invention.
