Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for measuring stress intensity factors of multi-round-hole multi-crack anisotropic material

A technology of stress intensity factor and anisotropy, applied in special data processing applications, complex mathematical operations, instruments, etc., can solve problems such as difficulty in obtaining high-precision solutions, dependence, and failure to consider the surface stress of round holes and cracks

Active Publication Date: 2021-05-07
CENT SOUTH UNIV
View PDF2 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, there are few studies on the problem of anisotropic multi-circular holes-multiple cracks
For example, Fotuhi and Fariborz used the supersingular integral equation method to calculate the multi-hole-multi-crack interaction stress intensity factor of orthotropic materials under far-field stress. However, this method needs to solve complex supersingular integral equations; Hwu et al. The relationship between the boundary element surface stress and the finite element nodal force, a boundary-finite element coupling method is proposed to calculate the anisotropic multi-hole-multi-crack problem, this method is not suitable for the case of round holes and surfaces subject to surface stress ; Dwyer et al. proposed a boundary function method to calculate the anisotropic multi-hole-multi-crack problem under far-field stress. Approximation
It can be seen that the above method is limited to the calculation of isotropic or anisotropic multi-hole-multi-crack interaction stress intensity factors under far-field stress, without considering the surface stress of round holes and cracks, let alone the arbitrary distribution of surface stress
Moreover, these methods for studying anisotropic hole-crack problems need to solve complex singular integral equations, or it is difficult to obtain high-precision solutions

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for measuring stress intensity factors of multi-round-hole multi-crack anisotropic material
  • Method for measuring stress intensity factors of multi-round-hole multi-crack anisotropic material
  • Method for measuring stress intensity factors of multi-round-hole multi-crack anisotropic material

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0053] Preferred embodiment 1, the specific steps of the method for measuring the stress intensity factor of the multi-hole multi-crack anisotropic material disclosed in this embodiment are as follows.

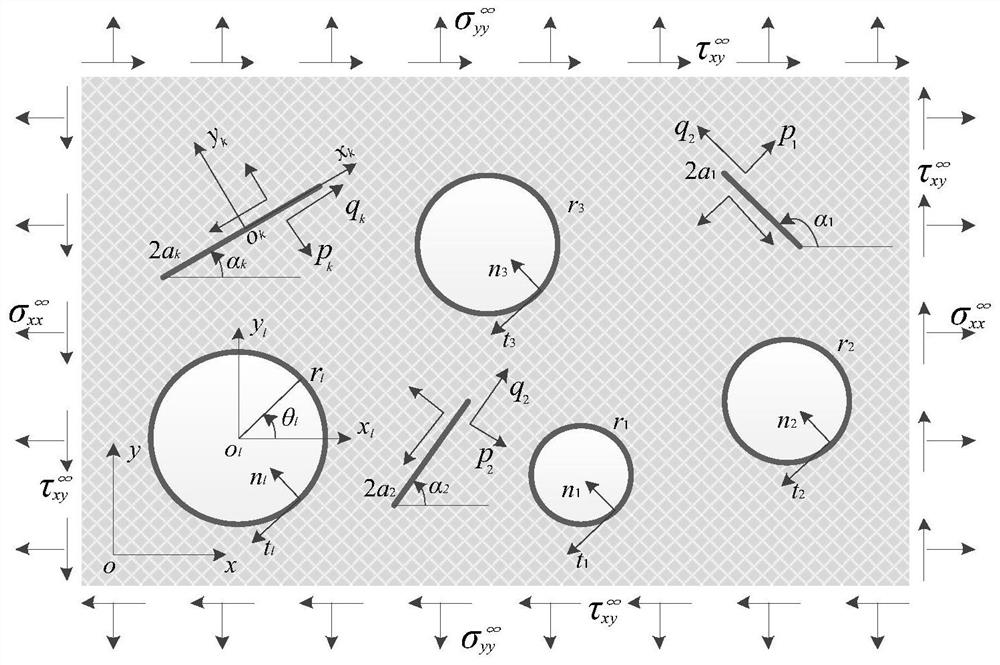
[0054] The first step is to construct an anisotropic body, such as figure 1 As shown, the anisotropic body contains L circular holes (radius r l ,l=1,2,3,…,L) and K cracks (half-length a k , inclination α k ,k=1,2,3,…,K), the far-field effect has uniform stress ( and ), the hole and the surface of the crack act on the surface of arbitrarily distributed normal stress and shear stress (n k , t k and p l ,q l ).

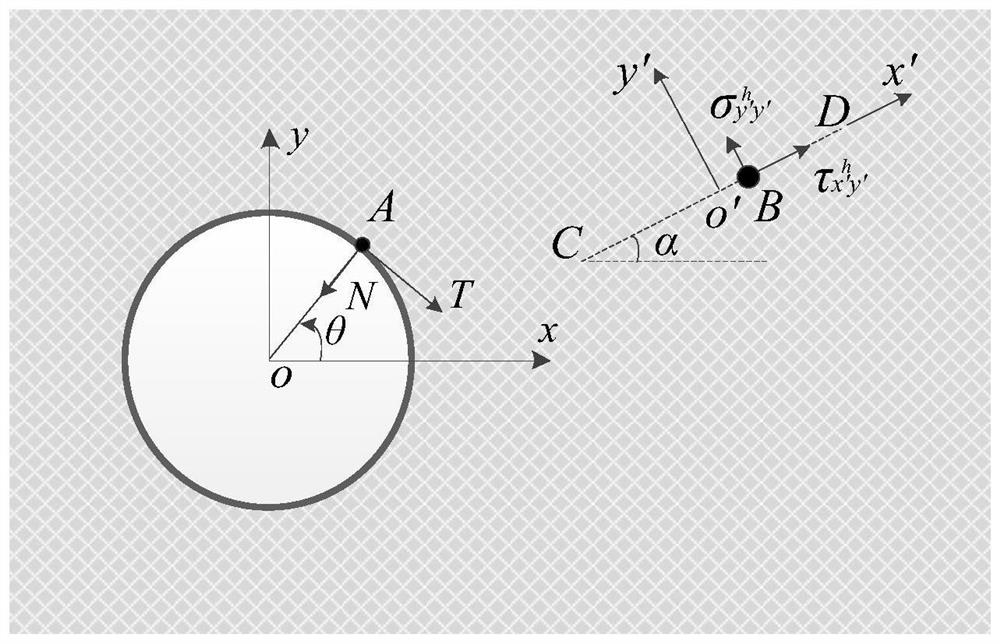
[0055] The second step is to construct a planar unit model with a single circular hole, such as figure 2 As shown, when the plane unit model contains a single circular hole (aperture r) and any point A(r, θ) of the anisotropic body acts on the concentrated force (N, T), any point B on the virtual crack CD (inclination angle α) normal and tangential stress ...

Embodiment 2

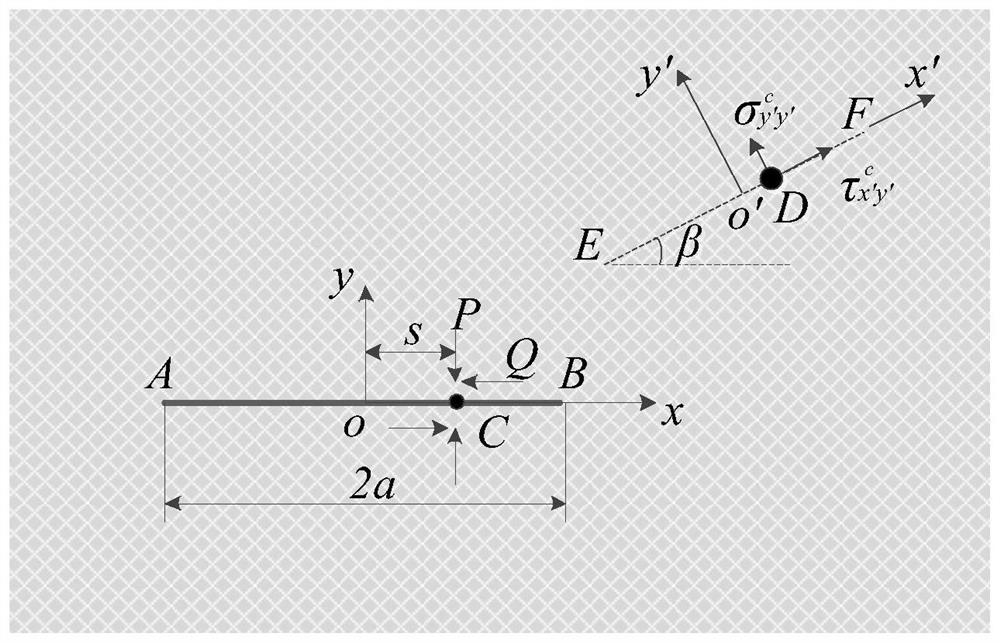
[0104] Preferred Embodiment 2. This embodiment is used to calculate isotropic materials. Such as Figure 4 As shown, construct an infinite isotropic flat plate (Poisson's ratio ν=0.3) containing a horizontal crack with a radius r and a length 2a (a=0.5r), and a uniform Brass stress σ acts on the vertical crack surface at infinity, s and t denote the horizontal and vertical distances between the center of the circle and the midpoint of the crack, respectively.

[0105] Let the two roots u of the characteristic equation of the anisotropic material j (j = 1, 2) are approximately equal, and the basic stress solution of the isotropic body with a single circular hole subjected to the concentrated force on the orifice surface is obtained approximately, and the crack inclination angle α in the basic solution is set to 0, and the stress caused by the concentrated force on the surface of the circular hole is obtained The normal and tangential stresses on the horizontal crack surface. ...

Embodiment 3

[0135] Preferred Embodiment 3. This embodiment can be used to calculate anisotropic materials. Such as Figure 5 As shown, construct an infinite anisotropic flat plate with a radius r and a length 2a (a=0.5r) inclined crack (inclination angle α=30°), and biaxial tensile stress acts at infinity Uniformly distributed surface stress n(n=-cos 2 θMPa), s represents the distance between the center of the circle and the midpoint of the crack. Anisotropic material properties are:

[0136]

[0137] S1: Make the crack inclination angle α=30 ° in the basic solution, obtain the surface normal direction and tangential stress of the inclined crack surface caused by the concentrated force on the surface of the circular hole;

[0138] S2: Determine the normal and tangential stresses on the surface of the circular hole caused by the concentrated force on the surface of the crack;

[0139] S3: Based on the derived basic solution and the stress boundary conditions of the circular hole an...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for measuring stress intensity factors of a multi-round-hole multi-crack anisotropic material. The method comprises the following steps of: constructing a plane unit model containing a plurality of round holes and a plurality of cracks by taking a to-be-measured material as a prototype, and defining boundary conditions; constructing a plane unit model containing a single round hole, and solving a stress basic solution of a concentrated force on the surface of the hole of the model according to a complex variable function Cauchy integral theory; constructing a plane unit model containing a single crack, and solving a stress basic solution of a concentrated force on the surface of the crack of the model according to a complex variable function Cauchy integral theory; according to the obtained stress basic solution and stress boundary conditions, obtaining an integral equation about the interaction surface stress of each round hole and each crack; discretizing the obtained integral equation into a linear algebraic equation; and deriving a stress intensity factor calculation formula of the plane unit model containing the single crack, and calculating a stress intensity factor of the plane unit model under the interaction of multiple round holes and multiple cracks by combining the solved crack surface interaction surface stress.

Description

technical field [0001] The invention belongs to the technical field of fracture mechanics, in particular to a method for measuring the stress intensity factor of anisotropic materials with many round holes and many cracks. Background technique [0002] In rock mass engineering such as slopes, water conservancy projects, tunnels, and mineral mining, natural rocks often show obvious anisotropy characteristics, and often contain defects such as cracks inside, and the existence of cracks causes cracks in the rock mass structure. The stress is more concentrated, which reduces the mechanical properties of the rock mass structure and greatly increases the engineering risk factor. Since arranging suitable round holes near the crack can effectively reduce the stress intensity factor of the crack tip, the drilling arrest method is a common and effective method to improve the engineering strength of rock mass. In addition, in the exploitation of shale gas, the hydraulic fracturing tec...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/20G06F17/11G06F17/15G06F17/16G06F111/10G06F119/14
CPCG06F30/20G06F17/11G06F17/15G06F17/16G06F2119/14G06F2111/10
Inventor 饶秋华易威孙栋良
Owner CENT SOUTH UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com