Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

LMI-based bionic flapping-wing aircraft H-infinity robust control method and system

A flapping-wing aircraft and robust control technology, applied in the field of bionic flapping-wing aircraft, can solve problems such as poor control accuracy, body differences, and enhanced model uncertainty

Active Publication Date: 2021-10-15
SHANGHAI JIAO TONG UNIV
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Traditional control methods such as linear quadratic regulation control and adaptive control have unsatisfactory tracking performance and stability when the modeling is inaccurate and the system is disturbed, especially the instantaneous lift generated by the flapping wing has high-frequency harmonics. component, so the control accuracy of the actual control process is poor
Moreover, the differences between the bodies of the current flapping-wing aircraft due to manufacturing errors will increase the uncertainty of the model, so it is necessary to develop a robust controller

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • LMI-based bionic flapping-wing aircraft H-infinity robust control method and system
  • LMI-based bionic flapping-wing aircraft H-infinity robust control method and system
  • LMI-based bionic flapping-wing aircraft H-infinity robust control method and system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

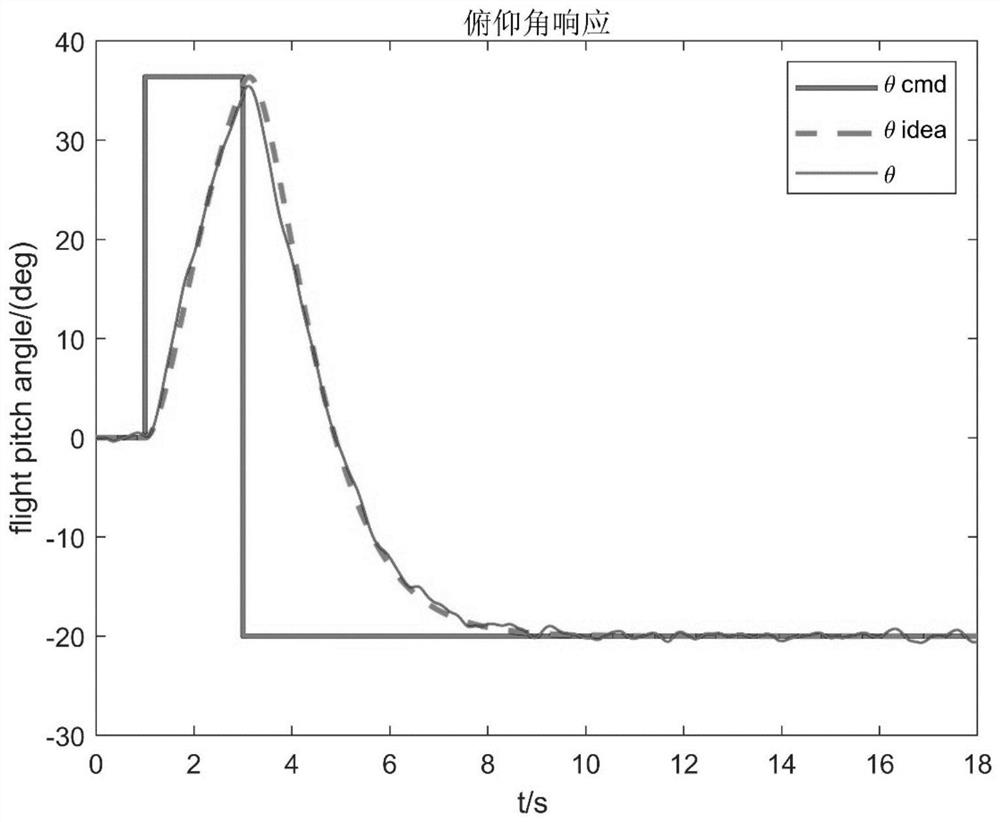
[0084] Aiming at the problem that the bionic flapping-wing aircraft has poor longitudinal stability and is easily affected by disturbances, the present invention aims at quantitatively describing the noise, disturbance and the uncertainty of the actuator for the aircraft model with uncertain parameters and external disturbances, and designs a bionic flapping-wing aircraft based on LMI. The H∞ robust control of wing aircraft, the final control system can eliminate the following error and resist the influence of disturbance and noise.

[0085] According to a kind of LMI-based bionic flapping-wing aircraft H∞ robust control method provided by the present invention, comprising:

[0086] Step S1: Establish a time-varying longitudinal dynamics model of the bionic flapping-wing aircraft;

[0087] Step S2: Periodically average the aerodynamic forces and moments of the bionic flapping-wing aircraft to obtain a longitudinal steady model of the nonlinear bionic flapping-wing aircraft;

...

Embodiment 2

[0172] Embodiment 2 is a preferred example of embodiment 1

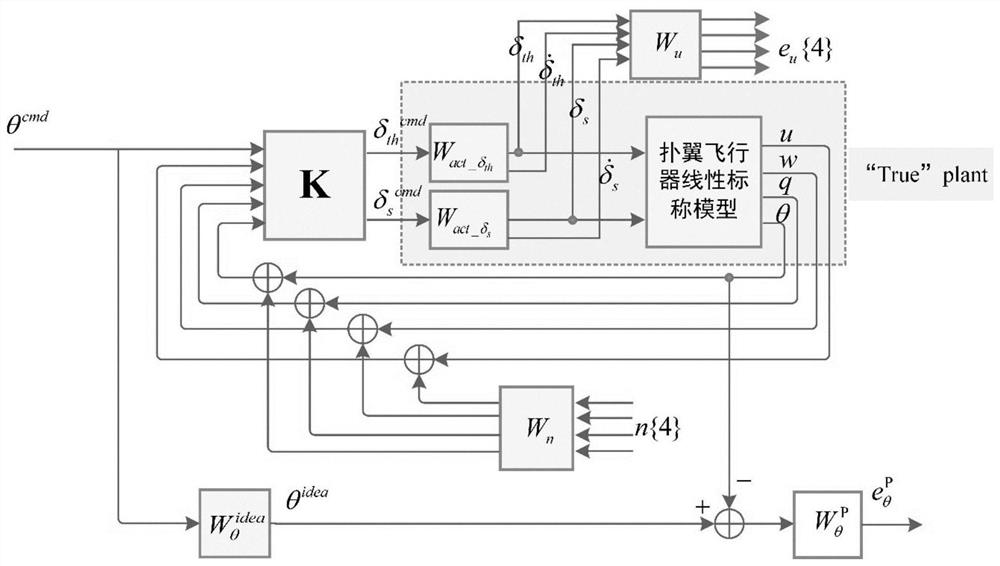
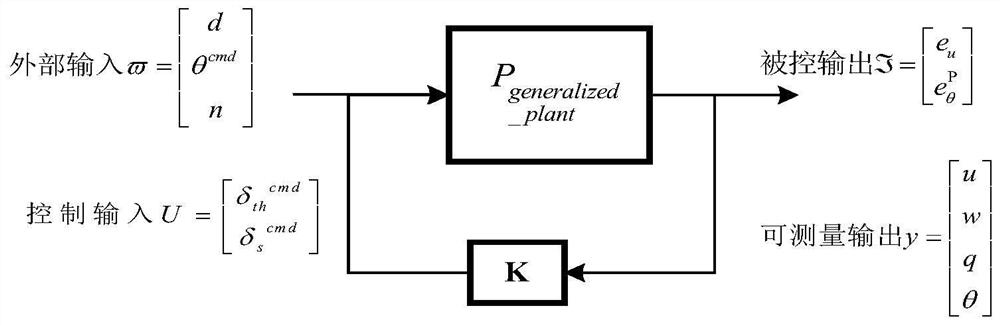
[0173] According to the LMI-based bionic flapping wing aircraft H∞ robust control method provided by the present invention, such as Figures 1 to 6 shown, including:

[0174] A steady longitudinal linear model of the aircraft is obtained according to the average theory. Using the hovering steady-state equilibrium operating point of the aircraft to apply small disturbances to the system input variable parameters one by one, the form of the small disturbance equation is obtained as:

[0175] Neglecting the effect of rotational circulation during wing flapping, then is approximately equal to 0, the state transition equation of the longitudinal nominal model can be abbreviated as Where B is the control matrix, and the control amount is the deflection angle δ of the linear servo that controls the pitching motion s and throttle amount δ th . The measured quantity is [u w q θ] T , the output equation is where t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an LMI-based bionic flapping-wing aircraft H-infinity robust control method and system. The method comprises the steps of establishing a bionic flapping-wing aircraft time-varying longitudinal dynamic model; performing periodic averaging on aerodynamic force and torque of the bionic flapping-wing air vehicle to obtain a longitudinal steady model of the nonlinear bionic flapping-wing air vehicle; linearizing the nonlinear longitudinal dynamic steady model at a balance point to obtain a linear nominal model; modeling noise, errors and dynamic characteristics of an execution mechanism of the bionic flapping-wing aircraft according to an actual control process, and designing a weight function according to the amplitude and frequency characteristics of the noise, the amplitude attenuation gain and frequency characteristics of the errors and the frequency characteristics of the dynamic characteristics of the execution mechanism; obtaining a generalized state space model of a controlled object according to the linear nominal model and the weight function, and converting a closed-loop system of the bionic flapping-wing aircraft into a standard form solved by an H-infinity controller; and solving a linear matrix inequality based on an LMI method to obtain a controller meeting robust stability and robust performance.

Description

technical field [0001] The present invention relates to the technical field of bionic flapping-wing aircraft, in particular to an LMI-based H∞ robust control method and system for a bionic flapping-wing aircraft. Background technique [0002] The bionic flapping-wing aircraft imitates the insects in nature, which is flexible and maneuverable, but has the characteristics of poor longitudinal stability, while the control amount produced by the current control mechanism is small, and the actuator has uncertainty, even exceeding 100% at some frequencies; The parasitic structural vibration generated by flapping wings of the insect-like flapping wing aircraft will generate noise, and the noise is similar to the flapping frequency, which is much smaller than the noise frequency caused by the motor rotation of the rotorcraft, which further increases the difficulty of control. [0003] Patent document CN112173101A (application number: 202011223949.X) discloses a hovering double flapp...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 张卫平郭倾城郑可心张逸晨郭彦含
Owner SHANGHAI JIAO TONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com