Method of encoding structured low density check code

A coding method and check code technology, which are applied in error detection coding using multi-bit parity bits, error correction/detection using block codes, digital transmission systems, etc., and can solve the problem that the shortest loop period is not well solved problem, to achieve good general applicability, good frame error rate performance, and the effect of reducing storage space

Inactive Publication Date: 2008-03-12
BEIJING UNIV OF POSTS & TELECOMM +1
View PDF0 Cites 47 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0016] However, how to construct such an LDPC code with as few short loops as possible and as large a shortest loop pe

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method of encoding structured low density check code
  • Method of encoding structured low density check code
  • Method of encoding structured low density check code

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0043] In order to make the objectives, technical solutions and advantages of the present invention clearer, the specific steps, features and performances of the method of the present invention are further described in detail below with reference to the accompanying drawings and embodiments.

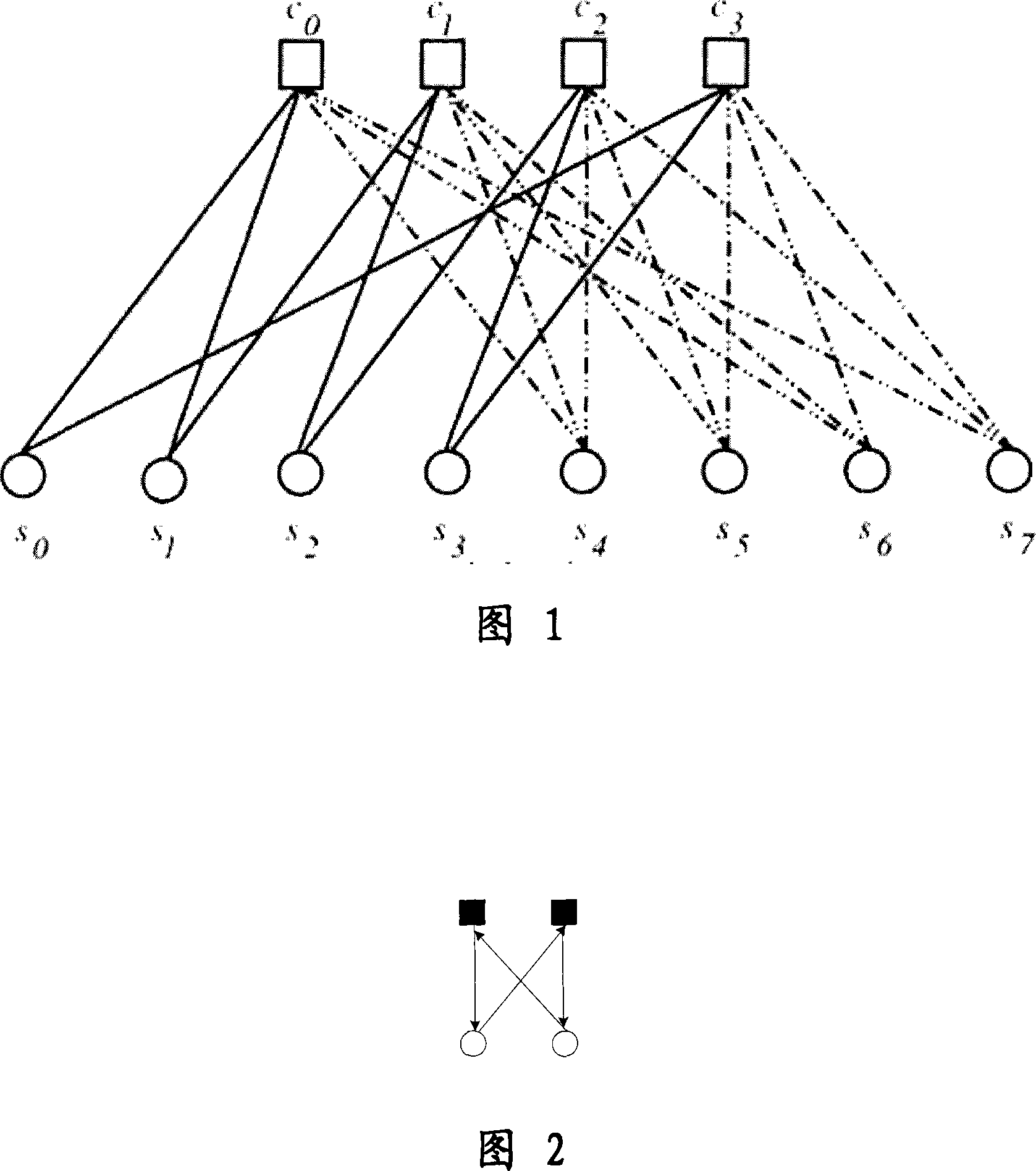
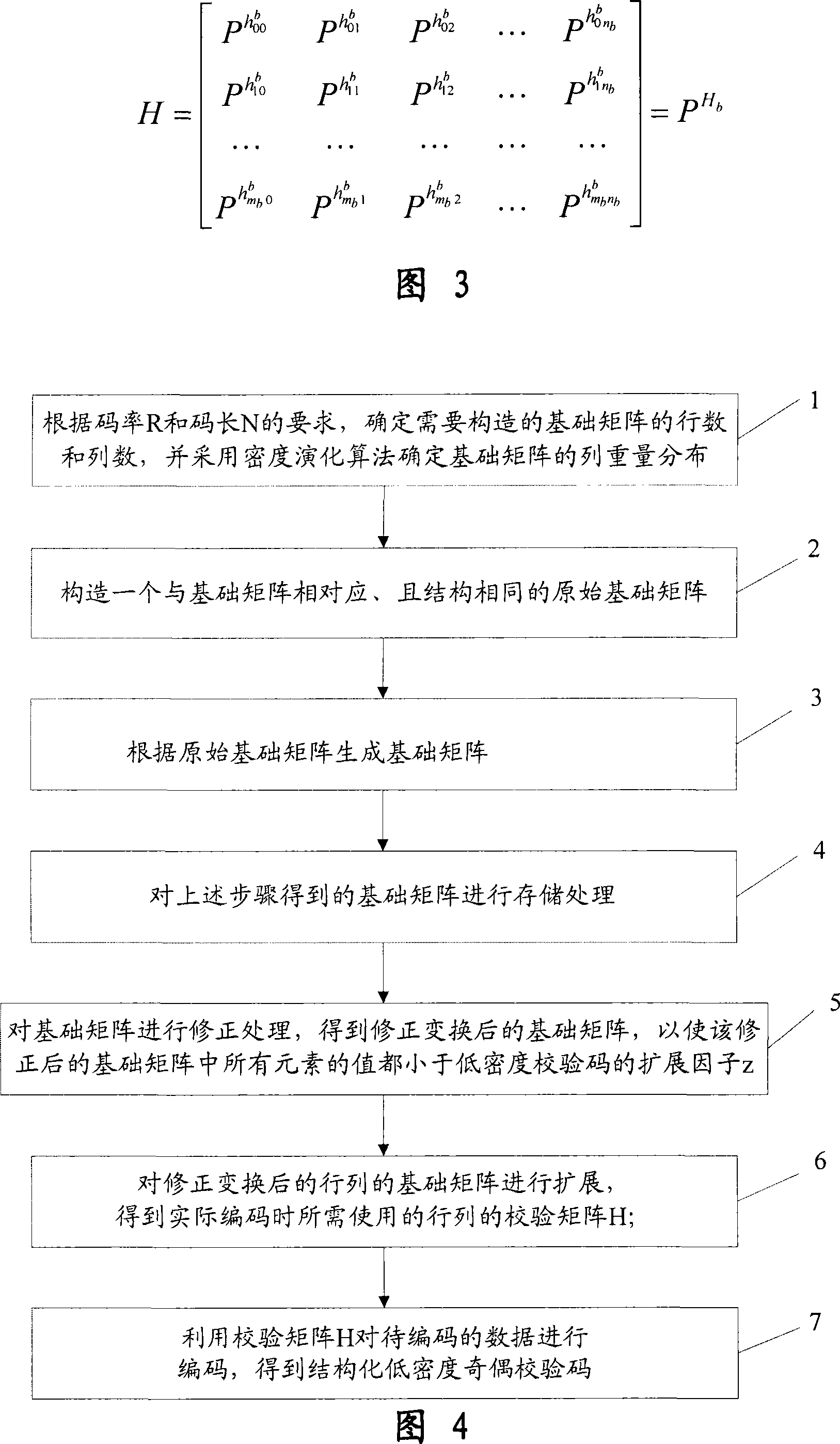
[0044] Referring to Fig. 3, the coding method of the structured low-density check code of the present invention is introduced, and the method comprises the following operation steps:

[0045] Step 1: Determine the basic matrix H that needs to be constructed according to the requirements of the code rate R and the code length N b the number of rows m b and the number of columns n b , and use the density evolution algorithm to determine the fundamental matrix H b The column weight distribution of The length M is a positive integer.

[0046] In the embodiment of the present invention, the selected code rate is 1 / 2, m b =16, n b = 32, and then use the density evolution algorithm to obt...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The utility model discloses a structured encoding method of low density parity checking code encoder. The rows mb and lines mb basic matrix Hb that needs to contracture are confirmed according to the requirements of code rate and code length, the weight distribution of the matrix Hb is determined by the density evolution algorithm. An original basic matrix Hb<>MASK<> that matches and has the same structure with the with the basic matrix Hb is formed; a basic matrix Hb is generated according to the original matrix Hb<>MASK<> for storage; then the basic matrix Hb is modified to become a basic matrix Hb' so as to make all element value inside the modified basic matrix Hb'smaller than the extension factor Z of the low density parity code; the modified basic matrix Hb'is extended to gain the parity matrix H of the (mb is multipled by Z) row and (nb is multipled by Z)that is used in actual encoding. Finally, the data is encoded with the parity matrix H to obtain structured low density parity checking code. The coding method is simple and practical and a low density checking code that has a plurality of code length and excellent frame error rate performance.

Description

technical field [0001] The invention relates to an encoding method of an error-correcting code in a digital communication system, to be precise, relates to an encoding method of a structured low-density check code, and belongs to the technical field of communication. Background technique [0002] The environment of data transmission in wireless mobile communication is usually affected by various factors such as channel fading, inter-symbol interference and time-varying noise. The introduction of channel coding (also known as error correction code) is to use error correction codes at the sending end and the receiving end respectively. The purpose of encoding and decoding data is to add error correction protection to the transmitted data to improve and ensure the transmission quality of the digital communication system. From the perspective of the construction method of channel coding, the basic idea is to add some artificial redundant code elements-check codes to the informat...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): H03M13/11H04L1/00
Inventor 吴湛击欧阳子月王文博郑辰雷旭胡炜
Owner BEIJING UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap