Non-probability set theory based bounded uncertainty structure static response upper and lower bound assessment method
A non-probabilistic set, uncertainty technology, applied in the field of evaluation of bounded uncertainty structural static response boundary, can solve the problem of too wide interval boundary, can not provide objective and effective data for structural reliability assessment and design, lose practical Application significance, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment
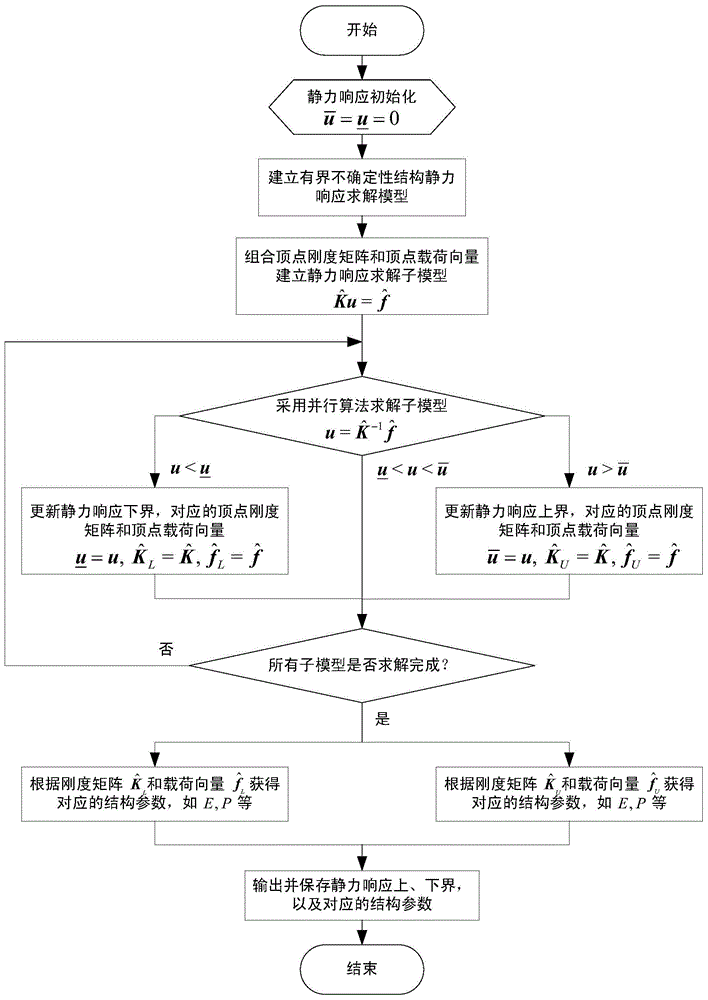
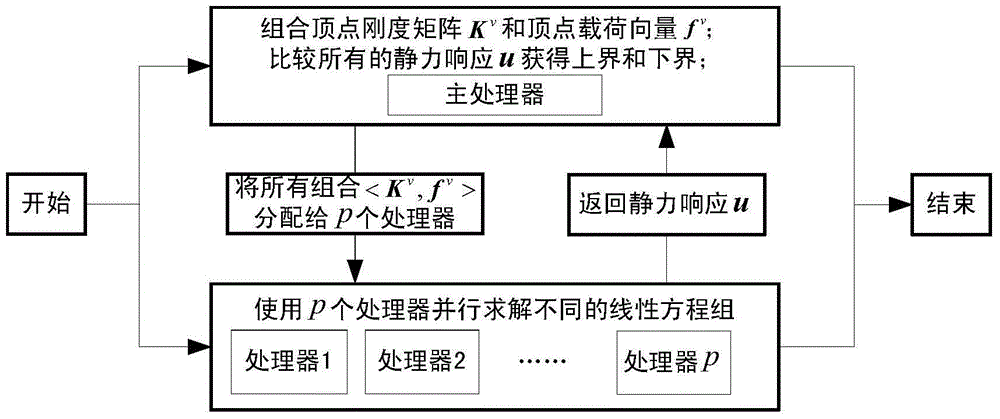
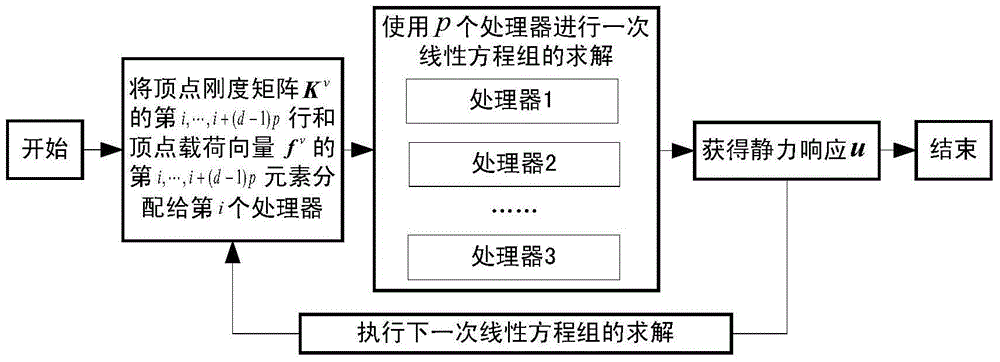
[0093] 1. Introduction to structural parameters and model analysis
[0094] In order to understand more fully the characteristics of this invention and its applicability to engineering practice, the present invention uses Figure 4 The two-segment rod shown is taken as an example for static response boundary evaluation. Figure 4 middle and Represent the stiffness coefficients of the two-section rods in the structure respectively, and the load p acts on the 2nd and 3rd ends of the rod respectively 1 and p 2 , due to manufacturing and measurement errors, stiffness coefficients and loads are bounded uncertainty parameters, and have p 1 = [49.5,50.5] and p 2 =[29.7,30.3], in this example, it is necessary to evaluate the static displacement boundary of the 2nd and 3rd ends of the rod.
[0095] 2. Evaluate the model
[0096] The governing equation of the static response of the two-section bar structure with bounded uncertainty is:
[0097] ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com