Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Quick design method of earth-moon L1 Lagrange point transfer orbit

A design method and technology for transferring orbits, applied in calculation, special data processing applications, instruments, etc., can solve the problems of long flight period and long calculation time of probes

Active Publication Date: 2016-08-31
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF3 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Designing this type of orbit requires a long calculation time, the engine is often on during the entire mission and the probe has a long flight period

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Quick design method of earth-moon L1 Lagrange point transfer orbit
  • Quick design method of earth-moon L1 Lagrange point transfer orbit
  • Quick design method of earth-moon L1 Lagrange point transfer orbit

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

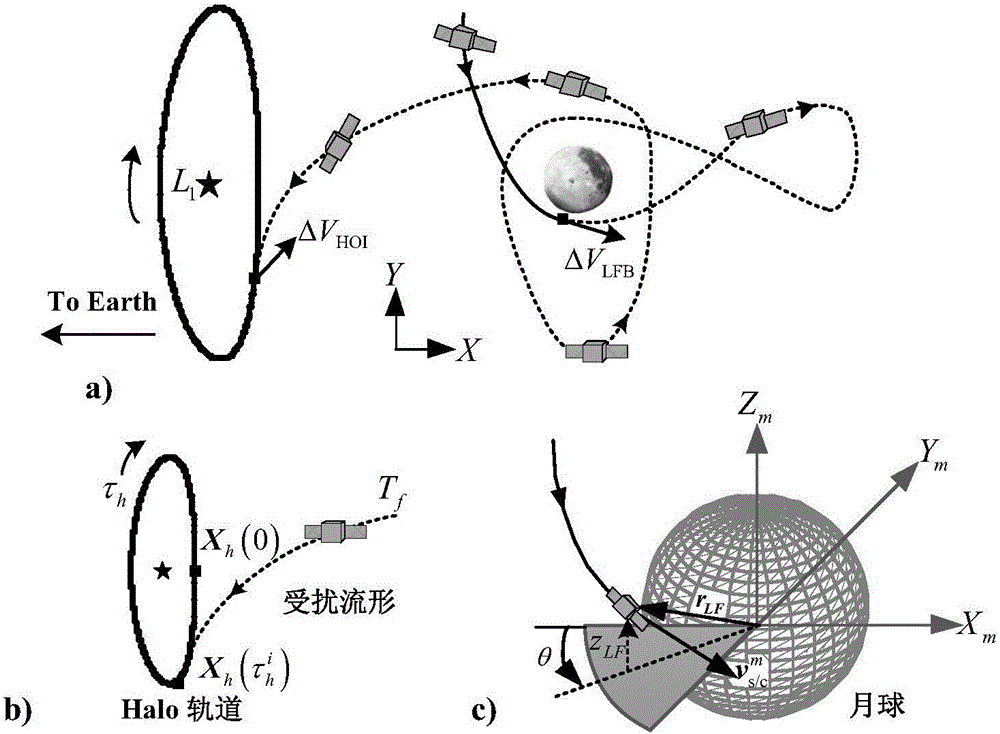
[0042] Such as figure 1 As shown, the invention discloses a method for quickly designing the transfer orbit of the Earth-Moon L1 Lagrangian point, aiming at the small normal amplitude A z = 5000km target Halo orbit design steps are as follows:

[0043] Step 1. The probe applies the first maneuvering pulse at the ideal orbit point of the target Halo orbit, and recursively from the L1 Lagrangian point Halo orbit to the position of the near-moon point that satisfies the leverage constraint;

[0044] When designing the orbit of the probe, it is necessary to consider the influence of the gravity of the earth and the moon in the coordinate system of the convergent center of mass. The dynamic equation can be expressed as:

[0045] x ·· - 2 y · = ∂ U ∂ x = x - ( 1 - μ ) r E S 3 ( x + μ ) - μ r M S 3 ( x - 1 + μ ) y ·· + 2 x · = ∂ U ∂ y = ...

Embodiment 2

[0066] Such as figure 1 As shown, the invention discloses a method for quickly designing the transfer orbit of the Earth-Moon L1 Lagrangian point, aiming at the large normal amplitude A z = 30000km target Halo orbit design steps are as follows:

[0067] Step 1. The probe applies the first maneuvering pulse at the ideal orbit point of the target Halo orbit, and recursively from the L1 Lagrangian point Halo orbit to the position of the near-moon point that satisfies the leverage constraint;

[0068] When designing the orbit of the probe, it is necessary to consider the influence of the gravity of the earth and the moon in the coordinate system of the convergent center of mass. The dynamic equation can be expressed as:

[0069] x ·· - 2 y · = ∂ U ∂ x = x - ( 1 - μ ) r E S 3 ( x + μ ) - μ r M S 3 ( x - 1 + μ ) y ·· + 2 x · = ∂ U ∂ y = ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a quick design method of an earth-moon L1 Lagrange point transfer orbit, and belongs to the technical field of spacecraft orbit design and optimization. The quick design method comprises the following steps: a detector applies a first-time maneuvering pulse to the ideal orbit entering point of a Halos orbit, and carries out reverse recursion on the first-time maneuvering pulse to a perilune position which meets leveraging constraints from the Halo orbit of the L1 Lagrange point; the detector applies a second-time maneuvering pulse to the perilune, and enters an earth-moon transfer orbit segment; and the detector applies a third-time maneuvering pulse and finally realizes earth parking orbit capture. Since the design method adopts an inverse integration strategy, a practical detector track departs from the earth, and finally, the Halo orbit of the earth-moon L1 Lagrange point can be achieved. The quick design method aims at different constraint sets, can automatically regulate the target orbit entering point of the Halos orbit, avoids the selection uncertainty of the orbit entering point, and has good reliability and practicality. In addition, speed increment required for finishing a task is small.

Description

Technical field [0001] The invention relates to a method for quickly designing the transfer trajectory of the Earth-Moon L1 Lagrangian point, in particular to a constraint selection method when a detector uses celestial body borrowing during interstellar navigation, and belongs to the technical field of spacecraft trajectory design and optimization. Background technique [0002] As a solid satellite in the solar system that revolves around the earth and is closest to the earth, the moon has become a research focus in the field of aerospace engineering and applications. The L1 translational point orbit that exists near the moon and is visible to the earth can be used as an ideal place for the probe to observe the moon and maintain communication with the earth (Farquhar, RW The utilization of haloorbits in advanced lunar operations[R].Technical Report NASA TN D- 6365, 1973). For the Earth-Moon L1 Lagrangian point transfer orbit mission, it can usually be divided into four stages: ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
CPCG06F30/15G06F30/367
Inventor 张景瑞曾豪祁瑞胡权张尧
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com