Quantification method for discrete Lorenz chaotic sequences

Abstract

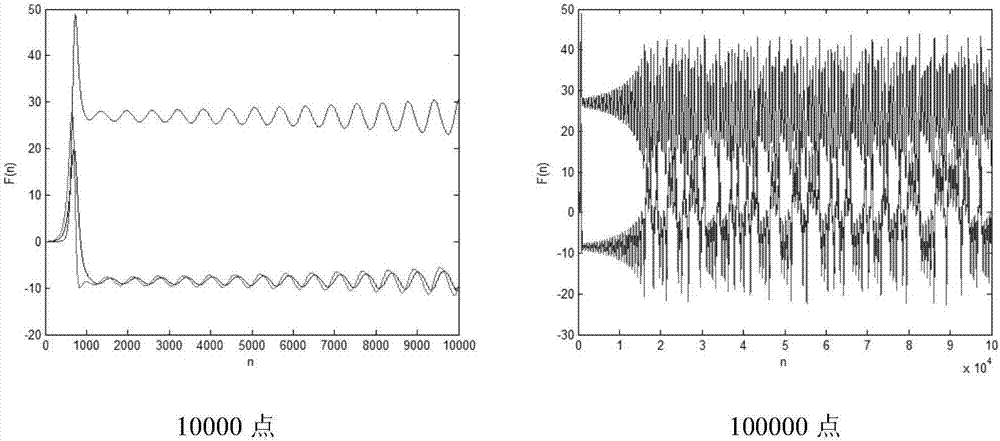
A quantization method for discretized Lorenz chaotic sequences, which takes the positive value of the real-valued sequence value; then moves the decimal point of the real-valued sequence value backward by 5 bits; removes the decimal part of all the real-valued sequence values, that is, rounds; converts the integer Partially divided by 10 to get the remainder, that is, to obtain the 5th digit after the decimal point of the original real-valued sequence, whose value is in the range of [0,9], adopt the threshold quantization method, take the expectation of all values ​​as the threshold, compare the value, if it is greater than this The threshold is taken as 1, and the threshold is taken as 0 if it is less than or equal to this threshold. 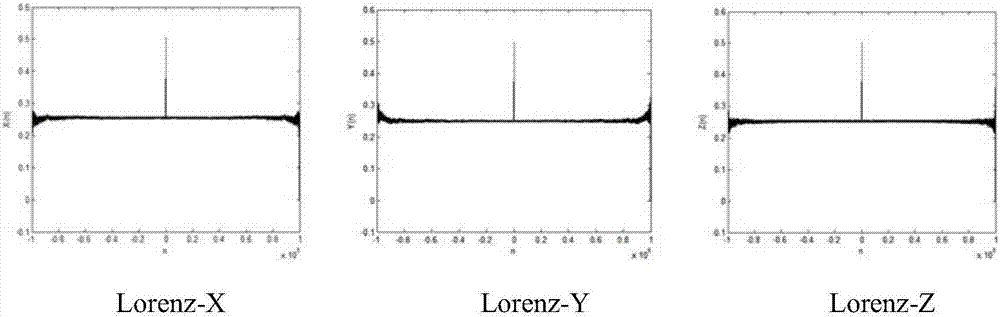The sequences in the X, Y, and Z directions generated by the Lorenz chaotic system are respectively quantized to obtain pseudo-random binary sequences in the three directions. The invention well overcomes the long-run phenomenon that occurs after the real-valued sequence of the Lorenz chaotic system is quantized by a typical quantization method, and the sequence exhibits excellent random characteristics, and has extremely high practical application value in the field of data encryption.

Description

technical field [0001] The invention relates to a quantization method for discrete Lorenz chaotic sequences. Background technique [0002] The three-dimensional Lorenz chaotic system equation is a model extracted by the American meteorologist Lorenz when he studied the atmospheric convection model. The system model is a ternary first-order nonlinear differential equation, which is different from the one-dimensional and two-dimensional chaotic systems. A chaotic system model that is continuous, not discrete. It is the most discussed and studied nonlinear dynamical system today, and it is a typical high-dimensional chaotic system, and its system equation is: [0003] [0004] where a, b, c are real parameters limited within a certain range of variation, and x, y, z are variables of the equation. [0005] After the continuous Lorenz chaotic system is discretized, a real-valued chaotic sequence is obtained, but in order to obtain a pseudo-random sequence that can be used fo...

AI Technical Summary

Problems solved by technology

This method is suitable for the case where the range of sequence values ​​is small. If the range is large, it is difficult to determine the value of m. If m is too large, the cost of specific hardware implementation will be too large. If m is too large Small, long run phenomenon will appear

[0015] according to figure 1 The distribution diagram of the discrete real-valued sequence of the Lorenz chaotic system is given, where the abscissa n represents the length of the sequence, F(n) represents the size of the iterative value of the sequence, the upper part is the distribution diagram of the Z(n) sequence, and the lower part is X The distribution diagram of (n) and Y(n) sequence, according to the distribution characteristics of sequence values ​​in the figure, is completely different from the distribution of one-dimensional and two-dimensional chaotic sequence values, and the range of sequence values ​​is very large, from -20 to 40 Between, the threshold quantization method and the interval quantization method are not applicable, and it is easy to generate a large number of long runs, and there will be a continuous increasing and decreasing trend between the parts, so the incremental quantization method is not applicable. According to the above analysis, although These typical quantization methods can quantify the Lorenz chaotic sequence, but there will be a large number of long-run phenomena in the quantization result, which will affect the randomness of the sequence, and then affect the security of the encryption result. Therefore, these three typical quantization methods are all Not suitable for quantization of Lorenz chaotic sequences

Images