Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

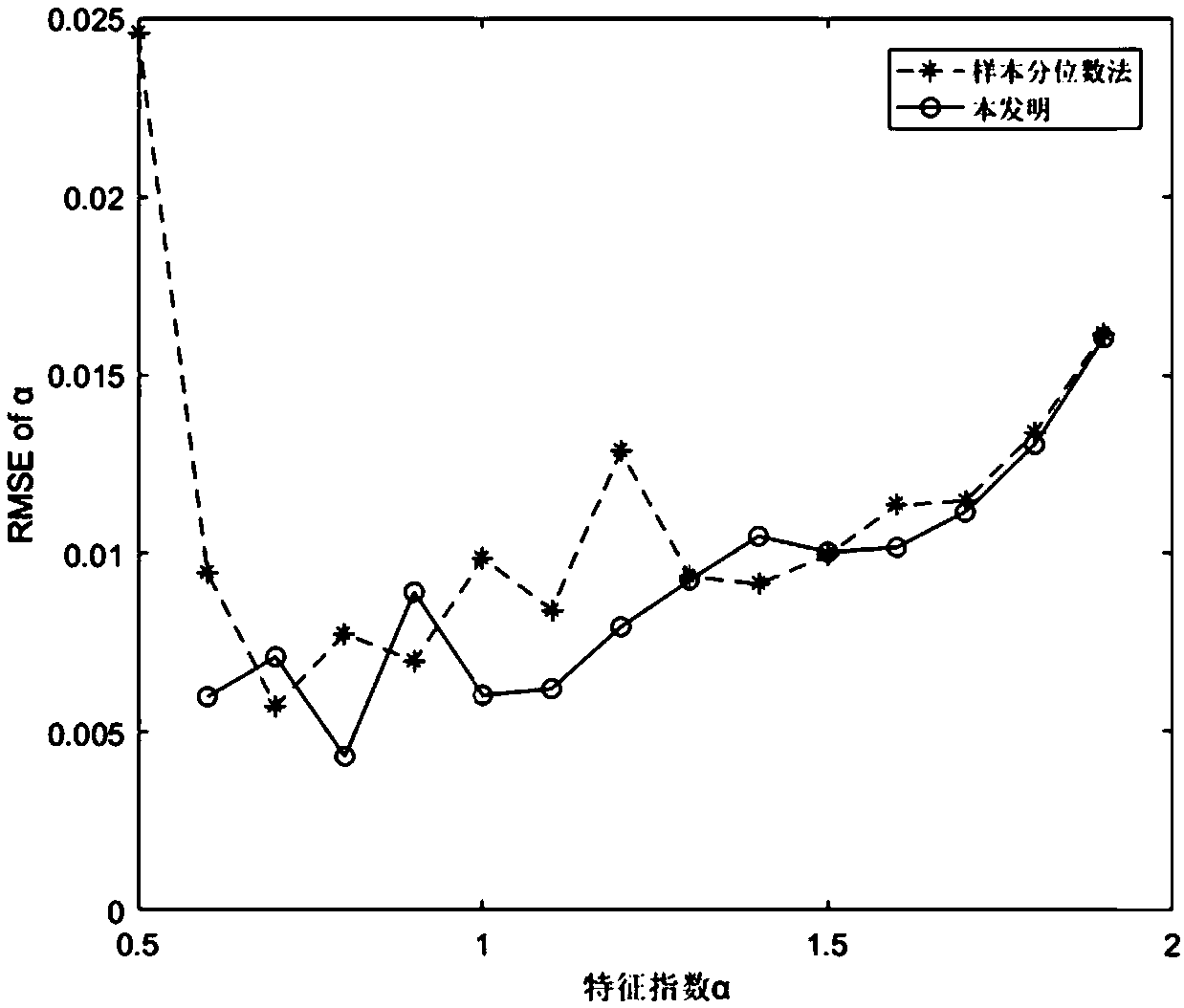
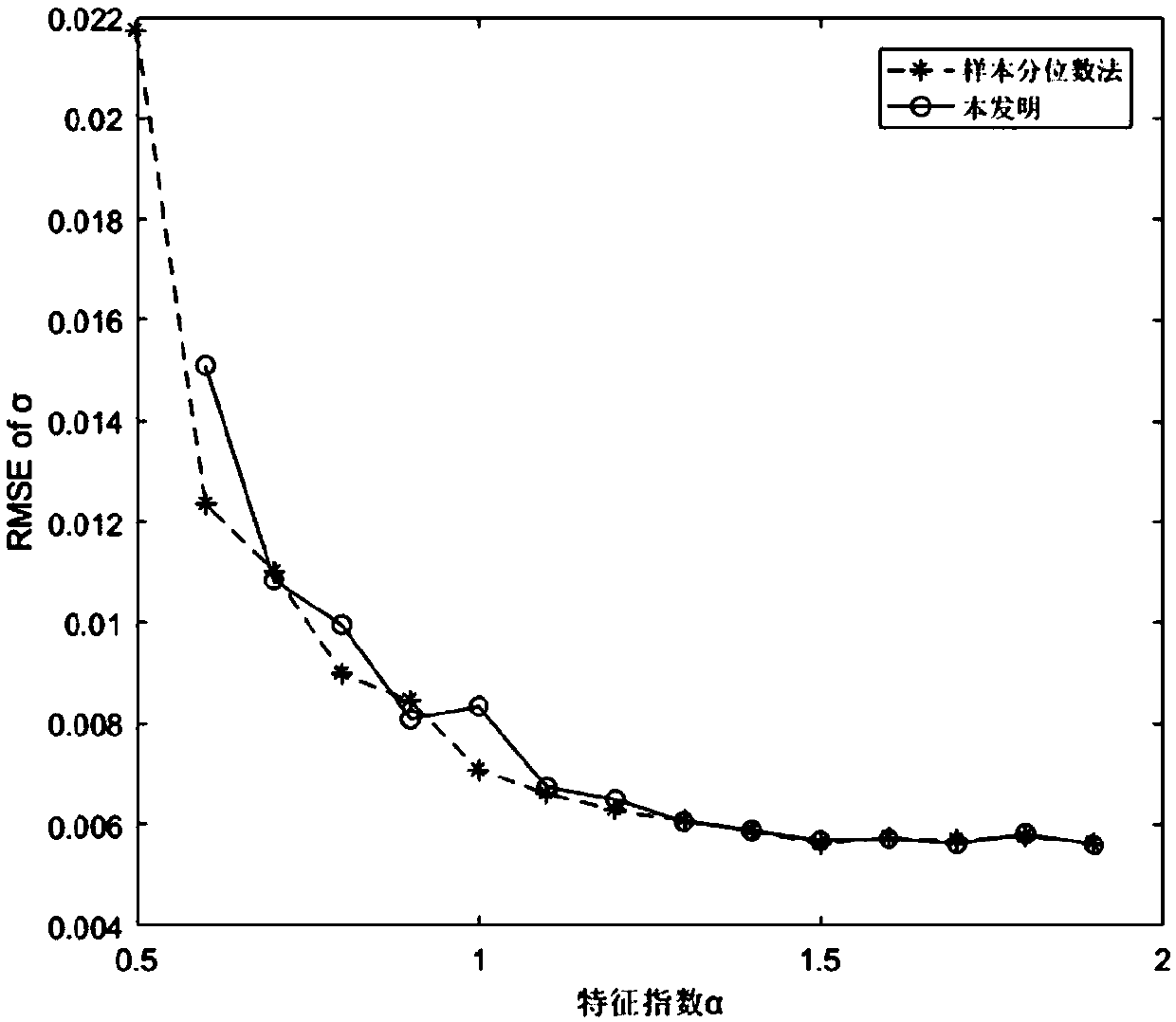
iteration method for SS distribution parameter estimation based on sample quantile

A technology of distribution parameters and quantiles, which is applied in the field of parameter estimation based on sample quantiles of symmetric α-stable distributions, can solve the problems of large quantile calculations, improve work efficiency, improve the accuracy of sample parameter estimation, and calculate The effect of increased complexity

Inactive Publication Date: 2019-03-26
CHONGQING UNIV OF POSTS & TELECOMM
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, due to the need to use quantiles, the calculation of quantiles in large-scale samples is large, so it is a big challenge for the computing speed and memory capacity of computers.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • iteration method for SS distribution parameter estimation based on sample quantile
  • iteration method for SS distribution parameter estimation based on sample quantile
  • iteration method for SS distribution parameter estimation based on sample quantile

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

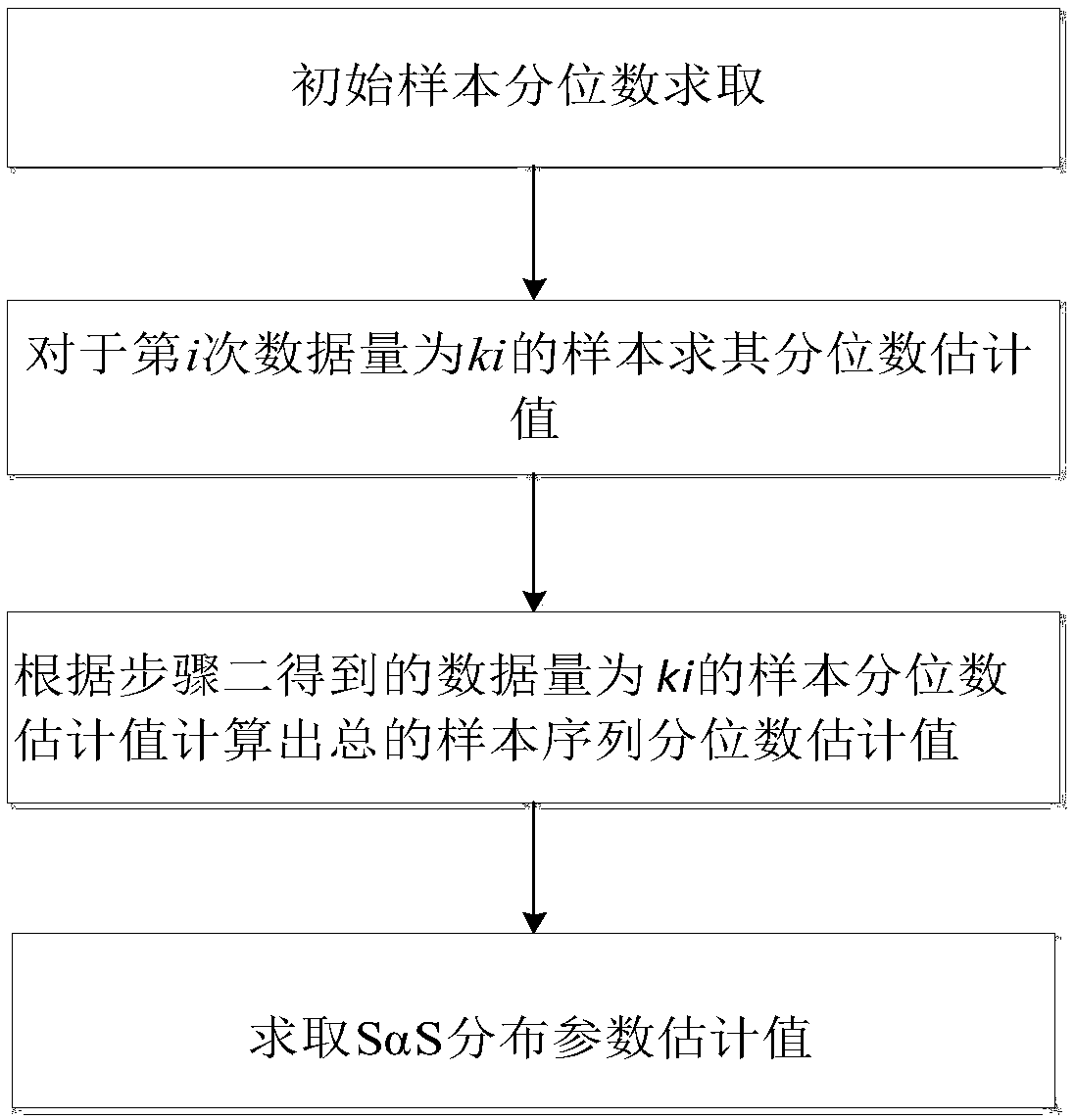
[0030] The present invention will be further described below in conjunction with accompanying drawing. refer to figure 1 , the present invention mainly comprises the following steps:

[0031] Step 1: For data size N 0 The sample, first find its 0.95, 0.05, 0.75, 0.25 quantile ε 0.95 (0),ε 0.05 (0),ε 0.75 (0),ε 0.25 (0).

[0032] The calculation of the sample quantile is based on the quantile estimation method of the empirical distribution, that is, the sequence X i The sample data in Sort to get order statistics x (1) ≤x (2) ≤…≤x (N) . definition:

[0033]

[0034] Then the quantiles under the empirical distribution are: [x] means to round x.

[0035] Step 2: According to the initial value of the quantile estimate obtained in step 1, iteratively calculate the estimated value of the sample quantile.

[0036] i) The amount of data added for the i-th time is k i , find its quantile estimate ε 0.95 (i),ε 0.05 (i),ε 0.75 (i),ε 0.25 (i).

[0037] ii) The qu...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention requests to protect an iteration method of SalfaS distribution parameter estimation based on a sample quantile method, and is mainly used for solving the problem of low execution efficiency of SS distribution parameter estimation based on the sample quantile method. The method mainly comprises the following steps: 1, for a sample with a certain data volume, firstly solving a quantileinitial value of the sample; 2, iteratively calculating a sample quantile estimation value according to the obtained sample quantile initial value; And 3, estimating a sample characteristic index alfa and a dispersion coefficient alfa according to the quantile estimation value. According to the method, the calculation complexity of the sample quantile estimation method is effectively reduced, theestimation precision is improved to a certain extent, and the method can meet the requirement for real-time estimation of the SalfaS distribution sample parameters.

Description

technical field [0001] The invention belongs to the field of communication signal processing, and in particular relates to a parameter estimation method based on sample quantiles of Symmetric α-Stable (SαS) distribution. Background technique [0002] In the current signal processing, Gaussian signals are mostly used as the background. This assumption is reasonable in many cases. However, in many actual scenarios such as underwater acoustic signal processing, biomedical engineering, low-frequency atmospheric noise signal processing and other signals often is non-Gaussian distributed. If Gaussian distribution is still used to describe these signals, it will lead to system performance degradation. The α-stable distribution, as a generalized Gaussian distribution, can well characterize such non-Gaussian signals with sharp peaks and thick tails. The concept of α-stable distribution was first proposed by Levy in 1925 in his study of the generalized central limit theorem. After ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/17G06K9/00
CPCG06F17/17G06F2218/00
Inventor 罗忠涛余达敏吴太锋黄利军
Owner CHONGQING UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com