Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for identifying fractional order viscoelastic model parameters based on multi-population genetic algorithm

A technology of model parameter identification and genetic algorithm, which is applied in the field of fractional viscoelastic model parameter identification, can solve the problem that the model parameter value cannot be identified

Active Publication Date: 2019-07-19
HARBIN INST OF TECH
View PDF8 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to solve the problem that the existing method cannot identify all parameter values ​​in the model when realizing the mutual conversion between creep compliance, relaxation modulus and dynamic modulus with the increase of parameters

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for identifying fractional order viscoelastic model parameters based on multi-population genetic algorithm
  • Method for identifying fractional order viscoelastic model parameters based on multi-population genetic algorithm
  • Method for identifying fractional order viscoelastic model parameters based on multi-population genetic algorithm

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

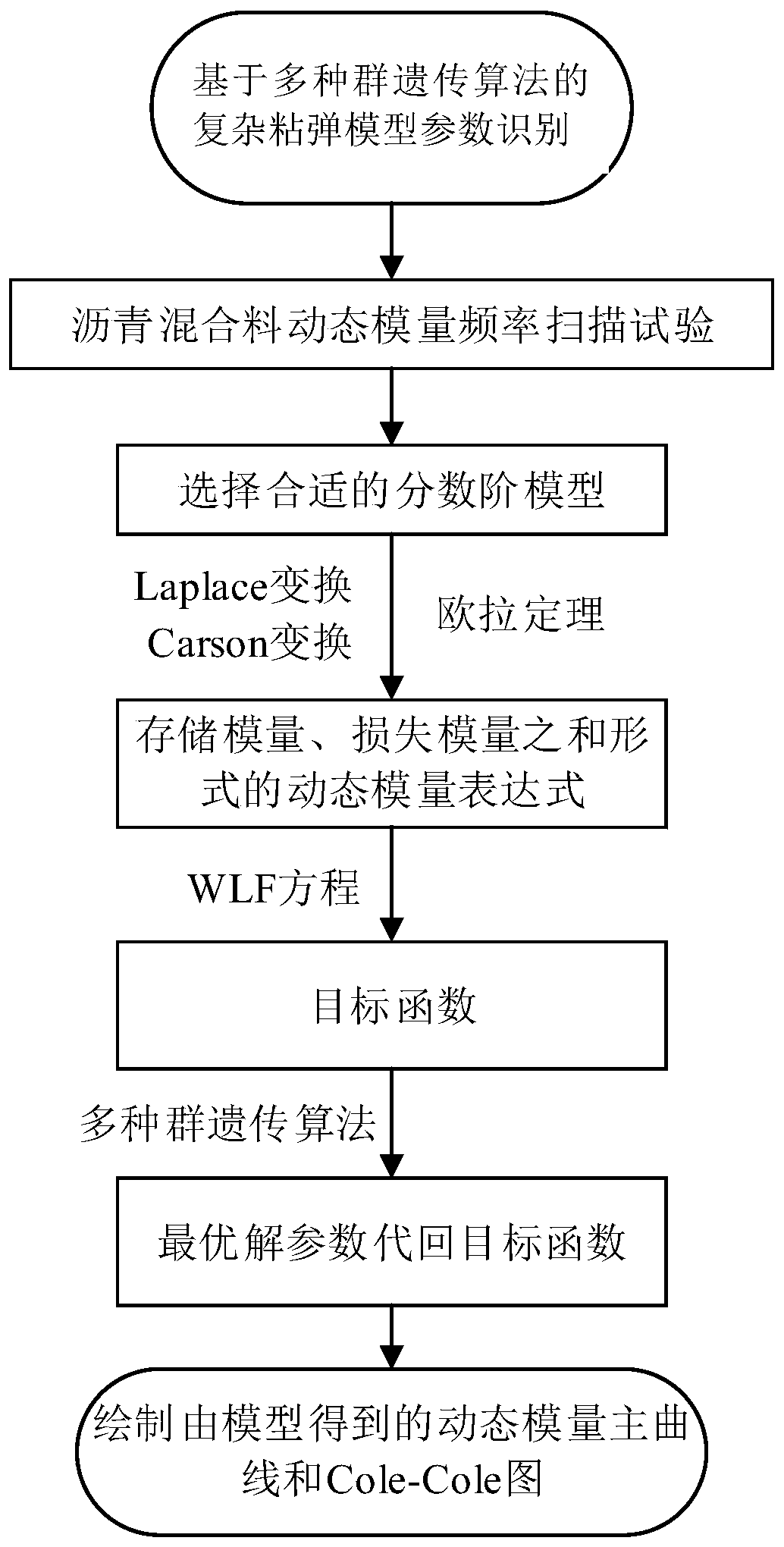
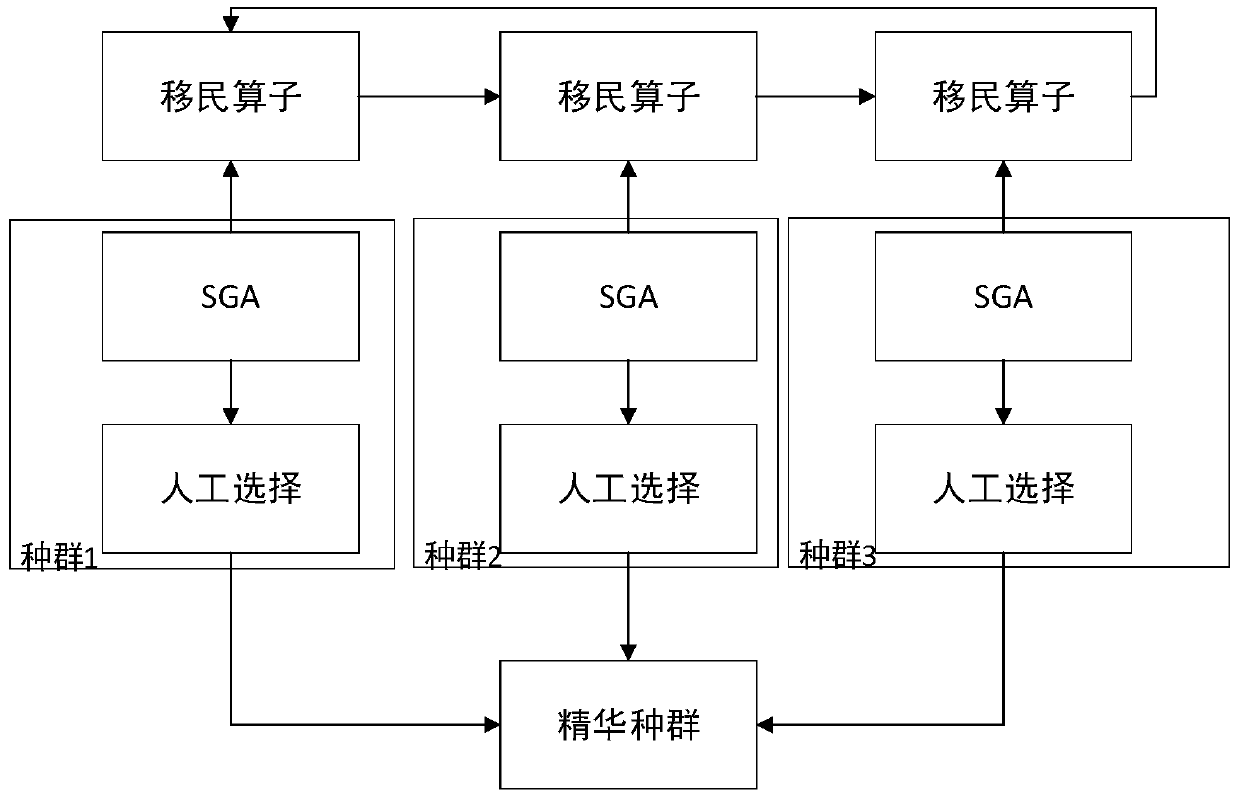
[0030] Specific implementation manner one: such as figure 1 , figure 2 with image 3 As shown, the method for identifying parameters of a fractional viscoelastic model based on multiple population genetic algorithms in this embodiment includes the following steps:

[0031] Step 1. Perform a dynamic frequency sweep test on the unaged asphalt at a temperature of [-30,-10,0,10,20,30,40,50] degrees Celsius, and obtain that each temperature point has a frequency of [1 ,5,10,15,20,25,30,40,50,60,70] dynamic modulus value at Hz;

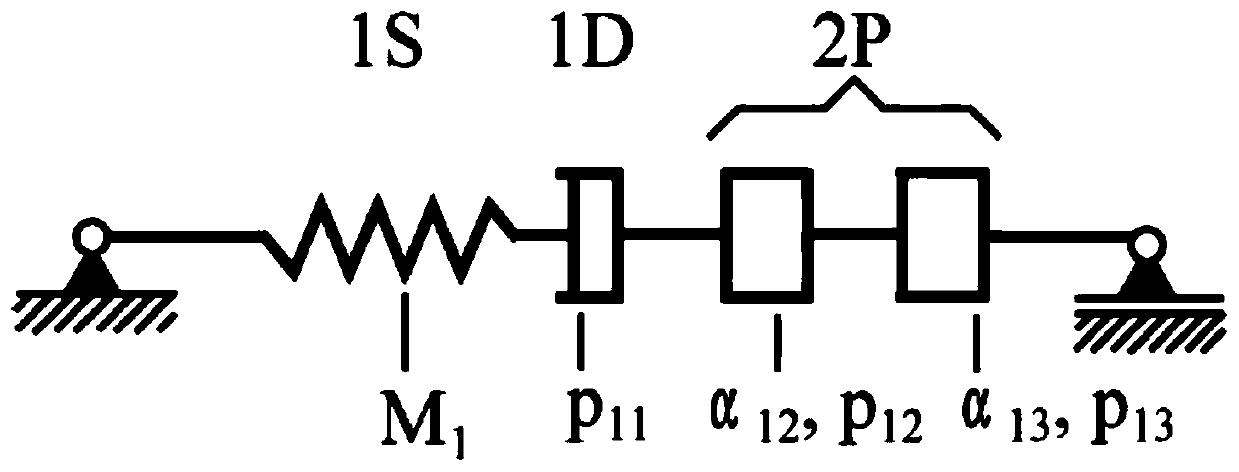
[0032] Step 2: Draw a Cole-Cole image (Cole-Cole image) according to the dynamic modulus value obtained in Step 1, and then select the fractional model as the 1S2P1D model based on the characteristics of the Cole-Cole diagram;

[0033] Combining the stress-strain relationship of the spring element, the viscous element and the fractional element in the 1S2P1D model, the stress-strain relationship of the 1S2P1D model in the Laplace domain can be obtained through La...

specific Embodiment approach 2

[0054] Specific embodiment two: this embodiment is different from specific embodiment one in that the stress-strain relationship of the spring element, the viscous pot element and the fractional element in the 1S2P1D model combined in the second step is through Laplace (Laplace) The transformation obtains the stress and strain relationship of the 1S2P1D model in the Laplace domain; the specific process is:

[0055] Combining the stress-strain relationship of the spring element, the viscous pot element and the fractional element in the 1S2P1D model, the stress-strain relationship of the 1S2P1D model in the Laplace domain is obtained by Laplace transformation as shown in formula (1):

[0056]

[0057] Among them: s is the independent variable in the complex number domain, Represents stress, Represents strain, M 1 Is the spring modulus, α 12 And α 13 Are all fractional sticky pot orders, p 11 Is the coefficient of linear viscosity, p 12 And p 13 All are the fractional viscosity coeff...

specific Embodiment approach 3

[0061] Specific embodiment three: this embodiment is different from specific embodiment two in that in the second step, Carson transform (Kasson transform) is performed on the stress and strain relationship of the 1S2P1D model in the Laplace domain to obtain the frequency domain expression of the dynamic modulus According to Euler’s theorem, the frequency domain expression of dynamic modulus is expressed as the sum of storage modulus and loss modulus; according to the influence of temperature on the parameters of the 1S2P1D model, the parameters of the 1S2P1D model considering the temperature effect are obtained; its specific The process is:

[0062] Carson transform formula (2) to obtain the frequency domain expression of dynamic modulus E(iω), the frequency domain expression of dynamic modulus is shown in formula (3):

[0063]

[0064] Among them: i is the imaginary unit, ω is the loading frequency;

[0065] According to Euler's theorem, the frequency domain expression of the dyna...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a method for identifying fractional order viscoelastic model parameters based on a multi-population genetic algorithm, and belongs to the technical field of constitutive behavior studies of bituminous mixtures. The problem that as for an existing method, all parameter values in a model cannot be identified during mutual transformation among the creep compliance, the relaxation modulus and the dynamic modulus is solved. According to the dynamic modulus value, the appropriate 1S2P1D model is selected, and through Laplace conversion, the stress-strain relationship of the 1S2P1D model is converted into the stress-strain relationship of the 1S2P1D model within the Laplace domain; then 1S2P1D model parameters considering the temperature effect are obtained; and finally, all the parameter values in the model are automatically obtained at a time based on the multi-population genetic algorithm, and thus the problem that as for the existing method, all the parameter valuesin the model cannot be identified during mutual transformation among the creep compliance, the relaxation modulus and the dynamic modulus is solved. The method can be applied to the technical field of the constitutive behavior studies of the bituminous mixtures.

Description

Technical field [0001] The invention belongs to the technical field of research on the constitutive behavior of asphalt mixtures, and specifically relates to a method for identifying parameters of a fractional viscoelastic model based on multiple population genetic algorithms. Background technique [0002] As a viscoelastic material, the mechanical behavior of asphalt and asphalt mixture is closely related to temperature and frequency, which conforms to the principle of time-temperature equivalence. As one of the mechanical parameters of viscoelastic materials, dynamic modulus is widely used in asphalt and asphalt mixture research. In order to obtain the dynamic modulus value of asphalt and asphalt mixture at any given temperature and frequency, the researchers used frequency scanning to obtain the dynamic modulus curve clusters of asphalt and asphalt mixture at different temperatures and specific frequencies. The principle of temperature equivalence translates the curve cluster...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01N33/42
CPCG01N33/42
Inventor 董泽蛟全蔚闻杨士真马宪永王彤旭
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com