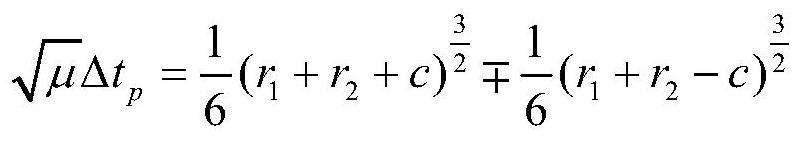Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

semi-major axis iteration space transfer orbit calculation method for Lambert orbital transfer problem based on Newton iteration

A technology for transferring orbits and calculation methods, which is applied in complex mathematical operations and other directions, and can solve problems such as poor timeliness and complex calculations

Pending Publication Date: 2020-10-09
HARBIN INST OF TECH
View PDF2 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, this method still needs to solve the hypergeometric function, the calculation is complicated, and the timeliness is poor

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • semi-major axis iteration space transfer orbit calculation method for Lambert orbital transfer problem based on Newton iteration
  • semi-major axis iteration space transfer orbit calculation method for Lambert orbital transfer problem based on Newton iteration
  • semi-major axis iteration space transfer orbit calculation method for Lambert orbital transfer problem based on Newton iteration

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

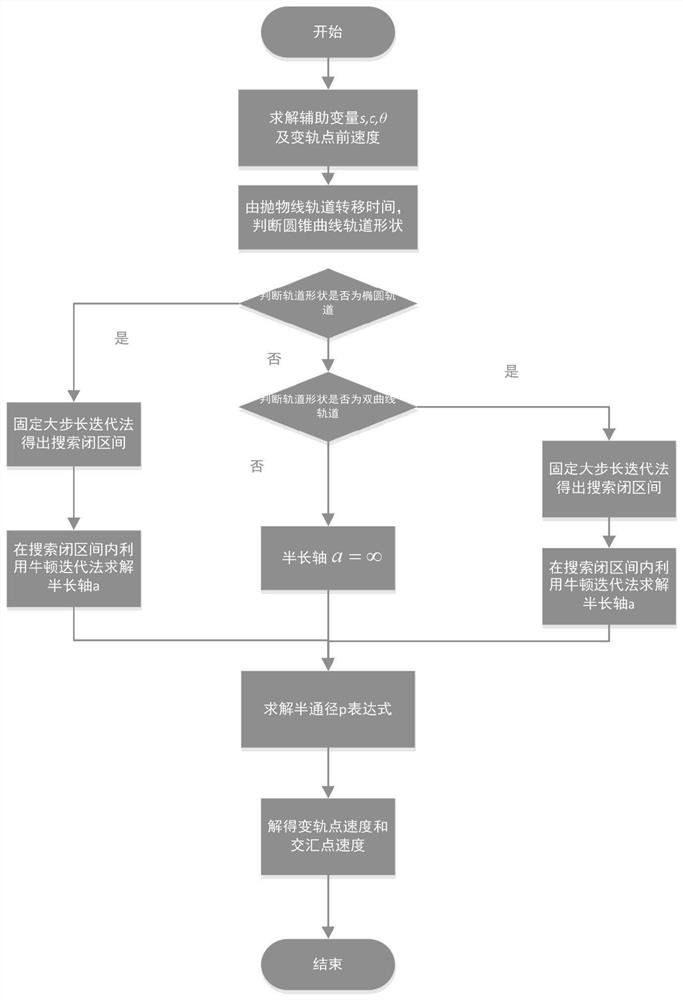
[0049] A semi-major axis iterative solution method for the Lambert orbit problem based on Newton's iterative thought, the semi-major axis iterative solution method comprises the following steps:

[0050] Step 1: Know the initial time t 1 The position vector of the mission vehicle on the initial orbit is r 1 , rendezvous time t 2 The position vector of the target aircraft in the target orbit is r 2 , calculate the transfer angle θ, auxiliary variable c and auxiliary variable s;

[0051] Step 2: According to the transfer angle θ, auxiliary variable c and auxiliary variable s calculated in step 1, determine the shape of the space transfer orbit of the aircraft;

[0052] Step 3: When the transfer time Δt is greater than the parabolic orbit transfer time Δt p , the transfer orbit is an elliptical orbit, and the elliptical orbit is solved;

[0053] Introducing the semi-major axis of the minimum energy ellipse When am , there is no elliptical transfer orbit between the two poi...

Embodiment 2

[0093] Next, select the orbit change position in the geocentric inertial system as r 1 =[-0.6058 0.3742 0.4001]×10 7 m, the intersection position is r 2 =[-1.5981 -2.1344 0.1212]×10 7 m as an example, the technical solution of the present invention will be further described in conjunction with the accompanying drawings.

[0094] Step 1: Calculate transfer angle θ=1.4707rad, auxiliary variable c=2.7121×10 7 m and auxiliary variable s=3.0990×10 7 m;

[0095] Using the orbital elements to solve the mission vehicle's orbit change position r at the initial moment 1 Velocity vector at

[0096] Calculate the distance r between the initial position and the intersection position 1 =||r 1 ||=8.168×10 6 m,r 2 =||r 2 ||=2.6691×10 7 m.

[0097] Step 2: Determine the track shape according to the transfer angle θ calculated in step 1, the auxiliary variable c and the auxiliary variable s;

[0098]

[0099] Where μ is the gravitational constant of the earth, and the parabol...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an improved solving method for a Lambert orbital transfer problem based on a Newton iteration thought. The method comprises the steps of 1, calculating a transfer angle theta,an auxiliary variable c and an auxiliary variable s; 2, determining the shape of the track according to the transfer angle and the auxiliary variable in the step 1; 3, when delta t is larger than delta tp, determining that the transfer orbit is an elliptical orbit, and carrying out solving; 4, when delta t is smaller than delta tp, determining that the transfer orbit is a hyperbolic orbit, and carrying out solving; 5, when delta t is equal to delta tp, determining that the transfer orbit is a parabola orbit, and carrying out solving; 6, expressing the Lambert orbital transfer problem analytical equation in the steps 3-5 as a function of a conic curve semi-major axis, and calculating a conic curve semi-drift diameter; 7, calculating orbital transfer point speed and intersection speed; and 8, proving the high efficiency and accuracy of the improved solving method for the Lambert orbital transfer problem based on the Newton iteration thought. The invention aims to improve the solving speed of the Lambert orbital transfer problem in spacecraft rendezvous.

Description

technical field [0001] The invention belongs to the technical field of spacecraft orbit design, and in particular relates to a method for calculating a semi-major axis iterative space transfer orbit of the Lambert orbit change problem based on Newton iteration. Background technique [0002] The Lambert orbit change problem, also known as the two-point boundary value problem, refers to the determination of the orbit of a spacecraft flying through two predetermined position vectors at a specified transfer time. The method to solve the space transfer orbit is not affected by the orbit height, orbit inclination and other conditions, and can solve the conic curve orbit between any two position vectors, and has wide applicability. From the Lagrange transfer time equation, it can be known that the relationship between the transfer time and the orbital elements of the transfer orbit is complicated, and it is impossible to directly determine the transfer orbit curve that meets the re...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/10
CPCG06F17/10
Inventor 王松艳晁涛蒋瑞晔杨明
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com