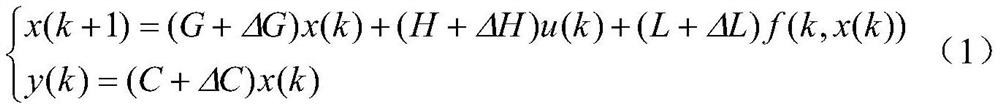Non-fragile optimal control method for Lipschitz nonlinear system

A nonlinear system, optimal control technology, applied in the direction of adaptive control, general control system, control/regulation system, etc., can solve the problems of uncertainty, system control performance impact, poor non-fragility, etc.

Active Publication Date: 2020-12-01
NANTONG UNIVERSITY
View PDF4 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Due to the influence of factors such as analog-to-digital conversion accuracy and word length, there are uncertainties when the controller is implemented by digital devices
However, the existing optimal control of Lipschitz nonlinear systems has the following pro...

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Non-fragile optimal control method for Lipschitz nonlinear system
  • Non-fragile optimal control method for Lipschitz nonlinear system
  • Non-fragile optimal control method for Lipschitz nonlinear system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0047] The present invention will be further explained below in conjunction with the accompanying drawings.

[0048] like figure 1 and figure 2 Shown, are respectively the flow chart and the structural diagram of the non-fragile optimal control of Lipschitz nonlinear system, the non-fragile optimal control method of a kind of Lipschitz nonlinear system of the present invention, comprises the following steps:

[0049] 1) The sensor samples the state of the Lipschitz nonlinear system with model uncertainty, converts it into a digital quantity with a logarithmic quantizer, and transmits it to the remote controller;

[0050] 2) Quantified data may be lost due to network congestion or interference during transmission to the controller. The Markov chain is used to describe the data transmission process, and the controller adopts corresponding control strategies according to the received data;

[0051] 3) The closed-loop system is described as a Markovian jump system. Based on the...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a non-fragile optimal control method for a Lipschitz nonlinear system. The method comprises the steps of 1) enabling a sensor to sample the state of the Lipschitz nonlinear system with model uncertainty, employing a logarithm quantizer to convert the state into a digital quantity, and transmitting the digital quantity to a far-end controller; 2) describing the data transmission process by adopting a Markov chain, and adopting a corresponding control strategy by the controller according to the data receiving condition; and 3) describing the closed-loop system as a Markovjump system, and designing a non-fragile infinite time optimal controller by using a linear matrix inequality based on the system model and performance indexes of the system. Aiming at the design problem of the non-fragile infinite time optimal controller of the Lipschitz nonlinear system with quantitative and incomplete measurement data, the invention provides the design method of the optimal controller, so that the system is stable, and the performance index functional takes the minimum value.

Description

technical field [0001] The invention relates to the field of optimal control, in particular to a non-fragile optimal control method for Lipschitz nonlinear systems. Background technique [0002] Lipschitz system is a kind of common nonlinear system, which can describe many physical processes. For example, robotic systems with sinusoidal terms, nonlinear systems satisfying Lipschitz conditions in a given interval, etc. When the sensor, controller, and actuator components of the system are distributed in a distant physical space, information transmission can be carried out through the network. The network-based control system has the advantages of low cost, good scalability, and convenient installation and maintenance, and has become the development trend of the control system. When the sensor measures and samples the state of the controlled system and converts it into a digital signal, it needs to be quantified. During the process of transmitting quantitative data to the c...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 马卫国许霞刘羡飞陈峰吴晓新
Owner NANTONG UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap