Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Adaptive control method and system for non-standard discrete-time nonlinear systems

A nonlinear system and adaptive control technology, applied in the field of control, can solve problems such as nonlinear parameterization uncertainty, non-standard discrete-time nonlinear systems cannot adapt to standard discrete-time nonlinear system control methods, etc.

Active Publication Date: 2022-04-01
ACAD OF MATHEMATICS & SYSTEMS SCIENCE - CHINESE ACAD OF SCI +1
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] An adaptive control method and system for a non-standard discrete-time nonlinear system proposed by the present invention can solve the problem that the non-standard discrete-time nonlinear system cannot adapt to the control method of the standard discrete-time nonlinear system, and there is an implicit relative order , nonlinear parametric uncertainty, and technical issues with non-affine control inputs

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Adaptive control method and system for non-standard discrete-time nonlinear systems
  • Adaptive control method and system for non-standard discrete-time nonlinear systems
  • Adaptive control method and system for non-standard discrete-time nonlinear systems

Examples

Experimental program
Comparison scheme
Effect test

example 1

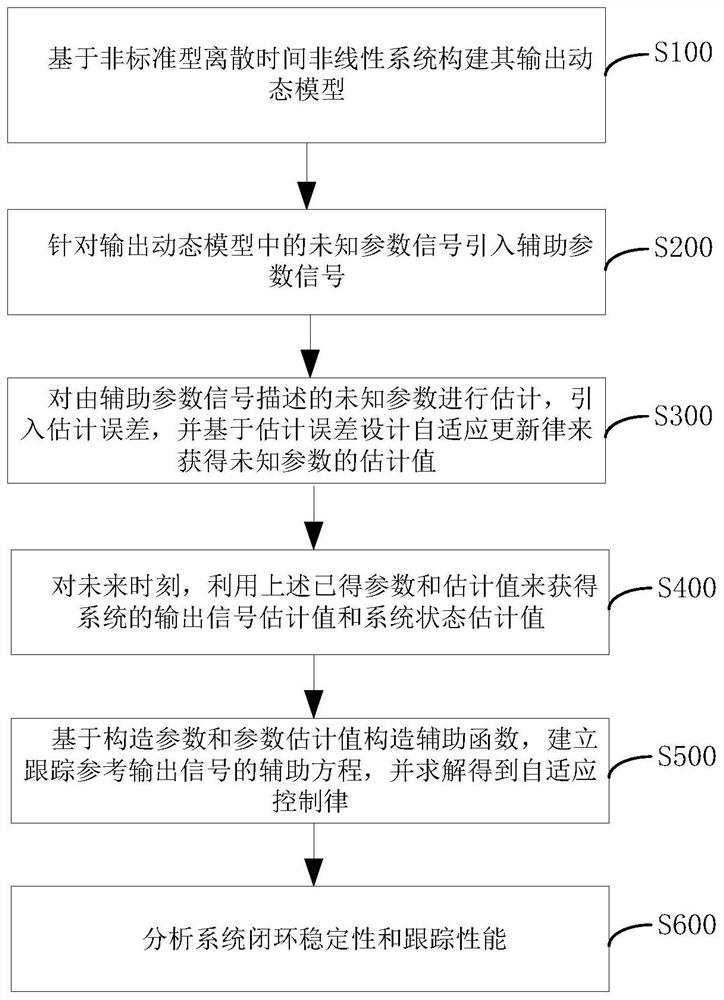
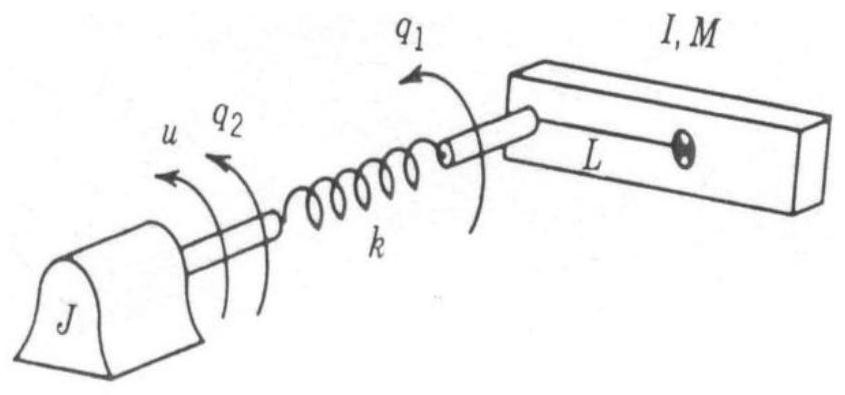
[0310] The self-adaptive control method of a non-standard discrete-time nonlinear system proposed by the invention can be effectively used in the design of the control law of a single-link flexible joint robot. For the sake of simplicity, the influence of damping is ignored in the actual control. First, a brief introduction to this type of robot system is given.

[0311] like figure 2 As shown, the motion equation of the single-link flexible joint robot is described as follows:

[0312]

[0313]

[0314] In the formula, q 1 ,q 2 is the angular position of the connecting rod and the motor, I and J are the moments of inertia, g is the acceleration due to gravity, k is the elastic constant of the joint spring, M and L represent the mass of the connecting rod and the position of the center of gravity, and u is the torque applied to the motor. First convert it into a mathematical model with control signals. make x 1 =q 1 , x 3 =q 2 , Then equations (53)(54) can ...

example 2

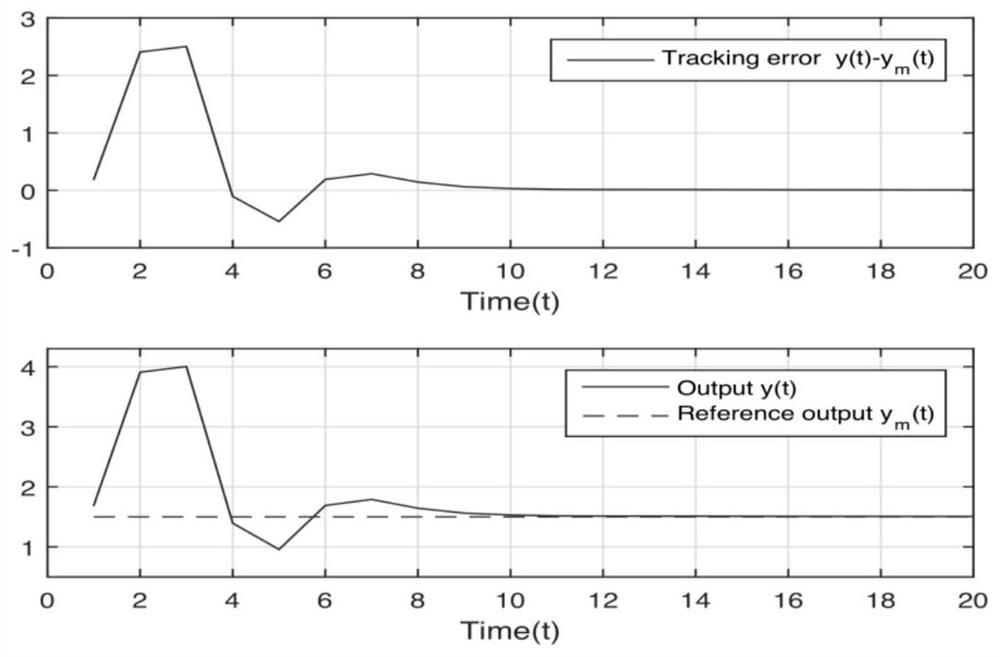
[0343] Take the following numerical simulation model as an example:

[0344]

[0345] x 2 (t+1)=0.2x 2 (t)5arctanx 1 (t)+1.3sinx 3 (t)

[0346] x 3 (t+1)=0.2x 3 (t)+1.6sinx 2 (t)

[0347] in, i=1, 2, 3 are the 3 state variables of the system, is the system input.

[0348] The system model is parameterized as

[0349]

[0350] y(t)=Cx(t)

[0351] in A known, and

[0352]

[0353] in

[0354] φ f (x(t))=[sinx 1 (t)cosx 3 (t), arctanx 1 (t), sin x 3 (t), sinx 2 (t)] T , C=[0,1,0] T . suppose C is unknown, φ f , φ g is known.

[0355] but,

[0356] Step 1: Suppose the system output y=x 2 (t), to establish a system output dynamic model;

[0357] It can be seen from the above that y(t+1)=0.2x 2 (t)+1.5arctanx 1 (t)+1.3sinx 3 (t) does not include the control input, so there are

[0358]

[0359] This means that y(t+2) contains both linear and nonlinear parameter uncertainties, and the nonlinearity depends on the control input. ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

An adaptive control method and system for a non-standard discrete-time nonlinear system of the present invention, including constructing its output dynamic model based on the non-standard discrete-time nonlinear system; introducing auxiliary parameter signals; introducing an estimation error, and based on the estimation error Design an adaptive update law to obtain the estimated value of the unknown parameter; for the future t+1 time, use the above-mentioned parameters and estimated value to obtain the estimated value of the output signal of the system and the estimated value of the system state; establish an auxiliary equation for tracking the reference output signal , and solve the adaptive control law; analyze the system closed-loop stability and tracking performance. The present invention first uses feedback linearization and implicit function theory to construct a standard form dependent on the relative order, then proposes a method based on adaptive parameter reconstruction to deal with the uncertainty of linear and nonlinear parameters in dynamic output, and finally constructs a key The implicit function equation is used to obtain the adaptive control law to ensure the closed-loop stability and asymptotic output tracking of the system.

Description

technical field [0001] The invention relates to the technical field of control, in particular to an adaptive control method and system for a non-standard discrete-time nonlinear system. Background technique [0002] Adaptive control is a control technique that can effectively deal with linear or nonlinear systems with parameter uncertainties. In recent years, adaptive control design has been widely used by applying techniques such as feedback linearization and BackStepping. Most existing adaptive control methods focus on standard-form nonlinear systems with explicit relative order structures and infinite zero structures. However, in practical applications, many system models are non-standard, and their system parameters or structures have large uncertainties, such as aircraft flight control systems and smart grid systems. Therefore, it is of great theoretical and practical significance to study non-standard nonlinear systems with parameter uncertainties. [0003] For stan...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 张纪峰张言军康宇赵延龙吕文君
Owner ACAD OF MATHEMATICS & SYSTEMS SCIENCE - CHINESE ACAD OF SCI
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com