Check patentability & draft patents in minutes with Patsnap Eureka AI!

Flexible Huffman tree approximation for low latency coding

A coding and coding technology, applied in the field of flexible Huffman tree approximation for low-latency coding, can solve problems such as inefficient computing resources

Pending Publication Date: 2022-03-22
MICROSOFT TECH LICENSING LLC
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0002] Although Huffman coding is optimal within the constraints of integer-length codes, Huffman coding can be inefficient in terms of the computational resources required to implement the algorithm
Additionally, Huffman coding poses interesting challenges for hardware implementations

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Flexible Huffman tree approximation for low latency coding
  • Flexible Huffman tree approximation for low latency coding
  • Flexible Huffman tree approximation for low latency coding

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

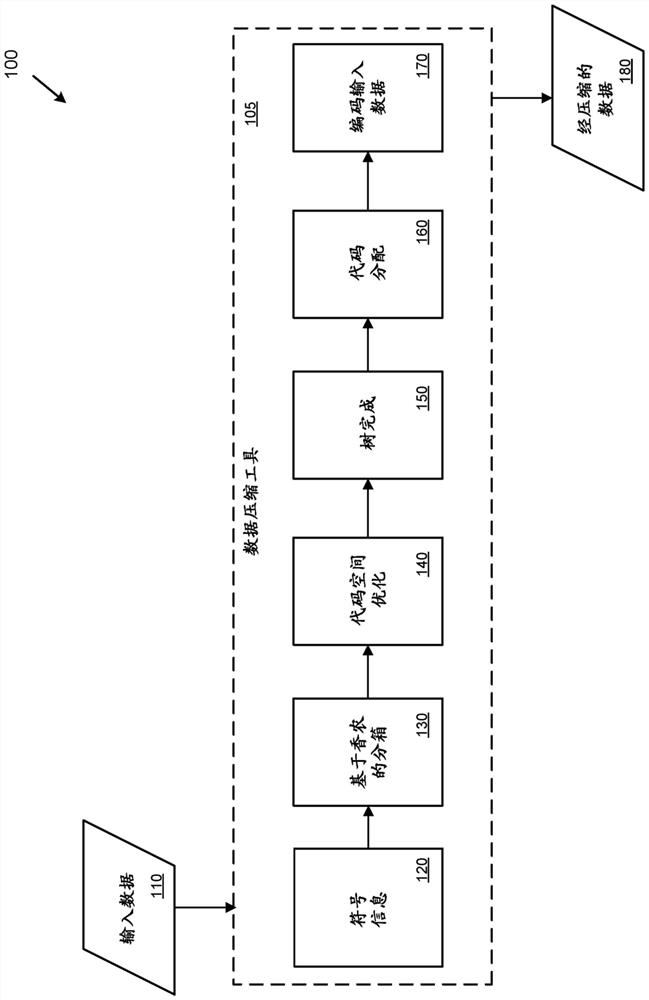
[0012] overview

[0013] As described herein, various techniques and technical solutions can be applied to approximate the Huffman coding algorithm (also known as Huffman algorithm, Huffman decoding, or Huffman coding) without using Huffman coding algorithm. For example, these techniques can be applied to encode (e.g., compress) data that gets close to (e.g., within one percent) Huffman coding but is more efficient (e.g., in terms of computing resources, latency, , hardware implementation, etc.) compression.

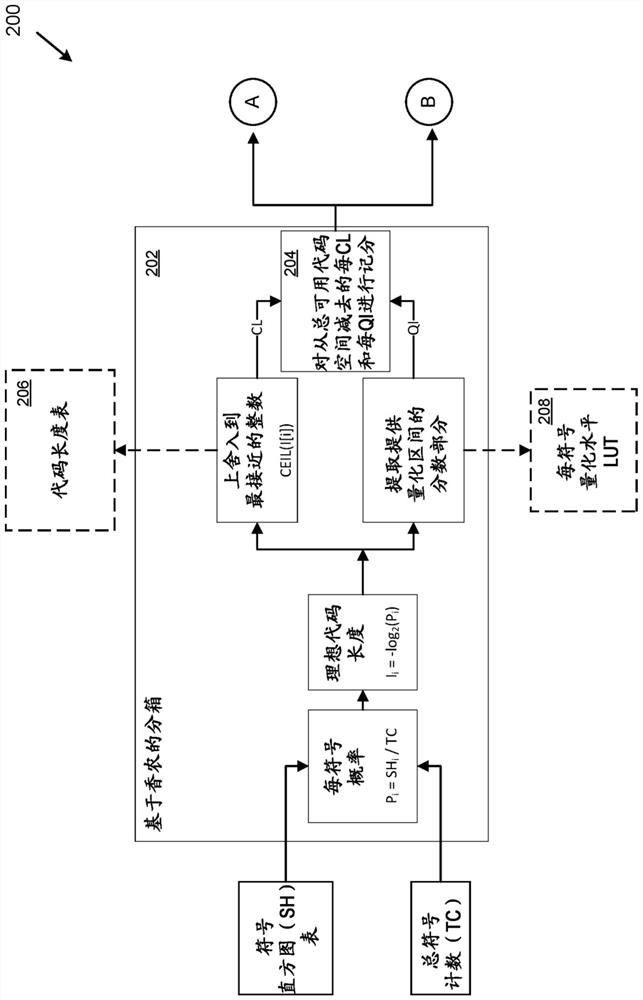
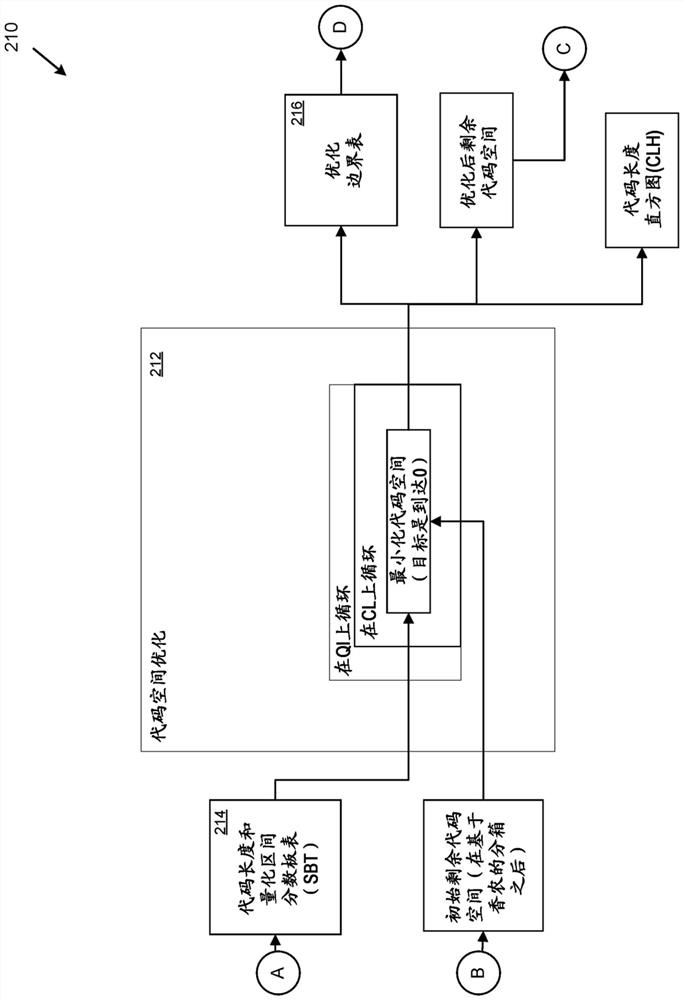
[0014] The technique involves a new algorithm for approximating the Huffman algorithm. The new algorithm is also known as Quantization Interval Huffman Approximation (QuIHA).

[0015] Depending on the implementation, the new algorithm may have one or more of the following properties:

[0016] * It yields good compression ratios, typically within 0.05% of true Huffman coding, which is provably optimal.

[0017] *It is suitable for high-speed implementation in Field P...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

Techniques are described for encoding symbols using a new algorithm that provides flexible Huffman tree approximation and can be used for low latency encoding. For example, a new algorithm may perform encoding using one or more of the following phases: Shannon-based binning, encoding space optimization, tree completion, and code allocation.

Description

Background technique [0001] Huffman trees have become the de-facto standard for optimized coding since their introduction. Their applications span a wide range from real-time multimedia to data center storage. Huffman structures are well understood, and many research articles explore Huffman tree properties and implementations in both software and hardware. In particular, Huffman coding is optimal within the constraints of integer-length codes from a formal algorithmic point of view. [0002] Although Huffman coding is optimal within the constraints of integer-length codes, Huffman coding can be inefficient in terms of the computational resources required to implement the algorithm. Additionally, Huffman coding poses interesting challenges for hardware implementation. Contents of the invention [0003] This Summary is provided to introduce a selection of concepts in a simplified form that are further described below in the Detailed Description. This Summary is not intend...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H03M7/40H03M7/30H03M7/42
CPCH03M7/4037H03M7/42H03M7/405H03M7/6017
Inventor T·H·黑尔B·A·布尔拉库
Owner MICROSOFT TECH LICENSING LLC
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com