Signing and decrypting method and system applied to cloud computing and based on SM2 algorithm

A cloud computing and algorithm technology, applied in the field of cryptography, can solve problems such as the inability to meet the low-latency application requirements of the cloud computing environment, the inapplicability of the cloud computing environment, and the large number of communications, and achieve a solution with less application requirements, low latency, and improved security. Effect

Active Publication Date: 2014-12-24
INST OF INFORMATION ENG CAS
View PDF5 Cites 65 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] However, the implementation of the above algorithms often has complex interactions and a large number of communications, which cannot meet the application re

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Signing and decrypting method and system applied to cloud computing and based on SM2 algorithm
  • Signing and decrypting method and system applied to cloud computing and based on SM2 algorithm
  • Signing and decrypting method and system applied to cloud computing and based on SM2 algorithm

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0030] In view of the problems in the prior art, the present invention proposes a signature scheme and a decryption scheme based on the SM2 algorithm that are suitable for cloud computing environments. SM2 algorithm is a standard commercial cryptographic algorithm, which is widely supported and used in cryptographic products.

[0031] In order to make the technical scheme of the present invention clearer and more comprehensible, the scheme of the present invention will be further described in detail below with reference to the drawings and embodiments.

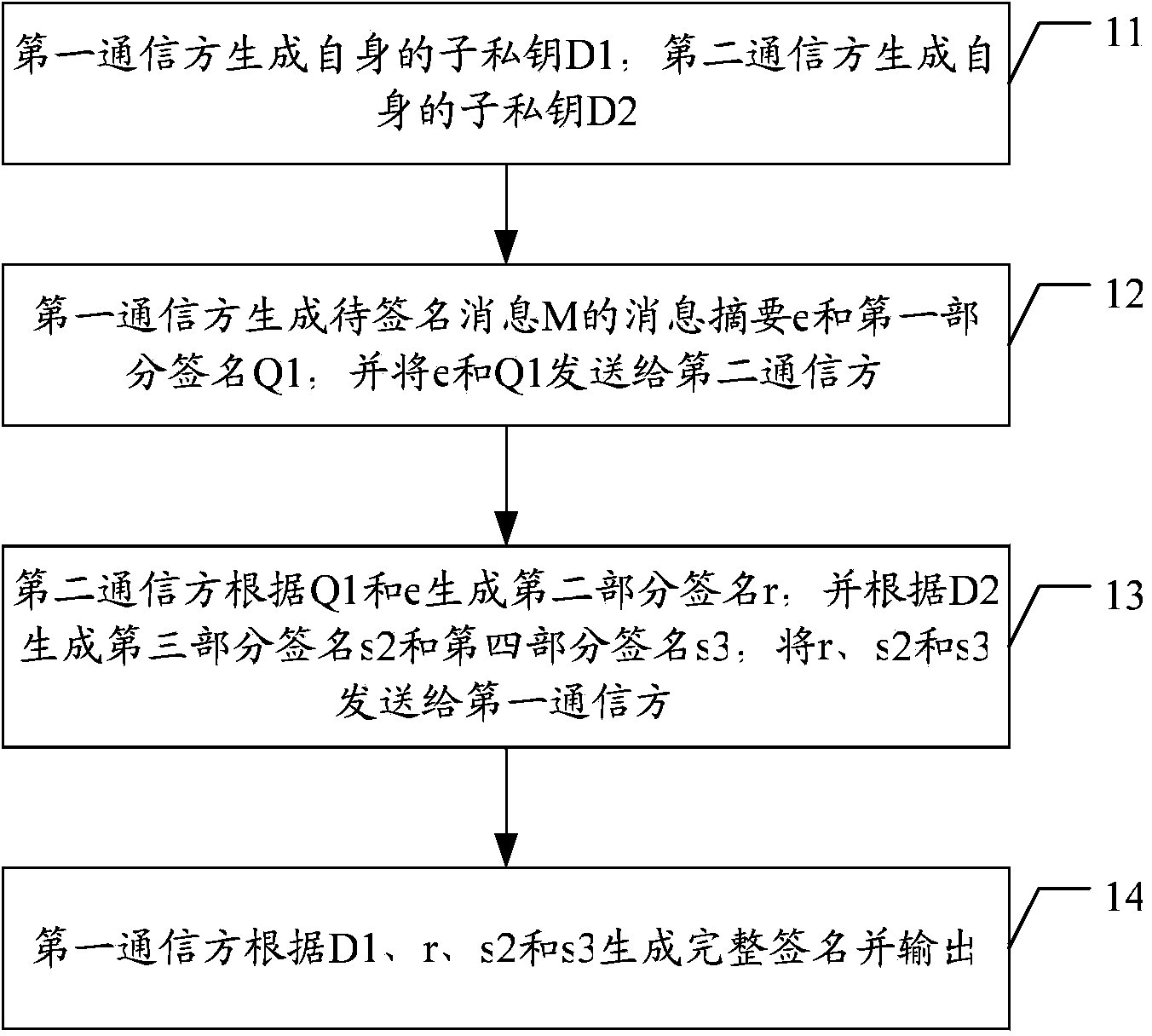
[0032] figure 1 It is a flowchart of an embodiment of a signature method based on the SM2 algorithm suitable for cloud computing in the present invention, such as figure 1 As shown, the following steps 11-14 are included.

[0033] Step 11: The first communicating party generates its own child private key D1, and the second communicating party generates its own child private key D2.

[0034] For ease of presentation, the first communic...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a signing and decrypting method and system applied to cloud computing and based on an SM2 algorithm. Specifically, two communicating parties store some private keys respectively, operation of signing, decrypting and the like can be carried out on information only when the two parties unite, the two communicating parties can not obtain any information about the private key of the opposite side, and therefore under the circumstance that an attacker invades any party, signatures can not be forged, or ciphertexts can not be decrypted, so that the safety of the private keys in the cloud computing environment is improved; moreover, in the signing and decrypting processes, the application requirements for low delay and less interaction in the cloud computing environment can be met with less interaction needing to be carried out between the two communicating parties.

Description

technical field [0001] The invention relates to the field of encryption, in particular to a SM2 algorithm-based signature and decryption method and system suitable for cloud computing. Background technique [0002] At present, digital signature and encryption and decryption technologies based on public key cryptography have been widely used in e-commerce, identity authentication and other applications, and have become an important tool to ensure information security, and the security and use of private keys are the basis for ensuring the security of these applications . [0003] In the cloud computing environment, the main resources are gathered on the server side, and the client side usually exists in the form of weak terminals, such as smart phones, etc. Such weak terminals usually store and use private keys in the form of software, so the security protection capability is poor . For example, if the private key is completely stored in a single file on the smartphone, the...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): H04L29/06H04L9/32H04L29/08
Inventor 林璟锵马原荆继武王琼霄雷灵光蔡权伟王雷
Owner INST OF INFORMATION ENG CAS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap