Sparse representation and empty spectrum Laplace figure based hyperspectral data dimension reduction method
A sparse representation coefficient and sparse representation technology, applied in the pre-processing field of hyperspectral data, can solve the problems of embedding structure influence, storage and calculation difficulties, and failure to consider the spatial structure of hyperspectral data, etc., to achieve fine spatial domain neighborhood structure, Break the limitation of data scale and improve the effect of the effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
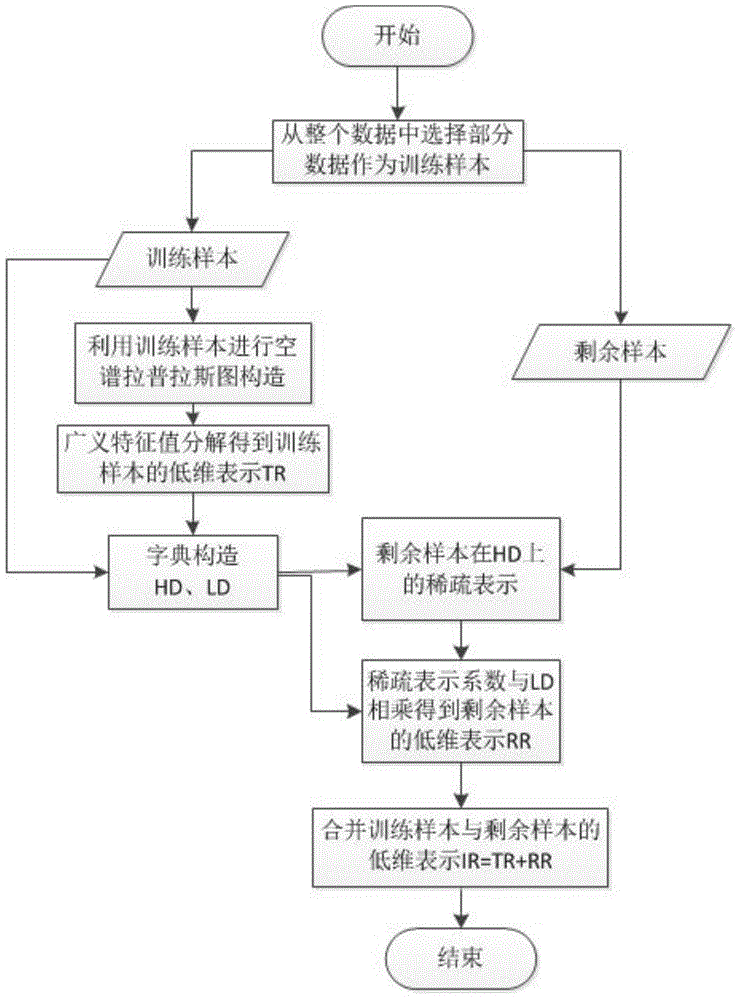
[0033] refer to figure 1 , the specific implementation steps of the present invention are as follows:
[0034] Step 1, select n data points from a piece of hyperspectral image data I as high-dimensional training samples, the dimension of hyperspectral data is p, and the value of n is determined by the scale of hyperspectral image data, taking 10% of the overall number above.
[0035] Step 2: Construct a space-spectrum Laplacian graph G by analyzing the training samples.
[0036] (2a) Construct the interspectral graph G1:
[0037] (2a.1) Spectral information divergence SID is a measure of spectral similarity between spectral data. Compared with the general Euclidean distance, it can better capture the similarity between spectral data, so spectral information divergence is used SID is used as the distance measure of the inter-spectral graph, so that the inter-spectral graph can more accurately capture the similarity relationship between training sample points. The definition...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com