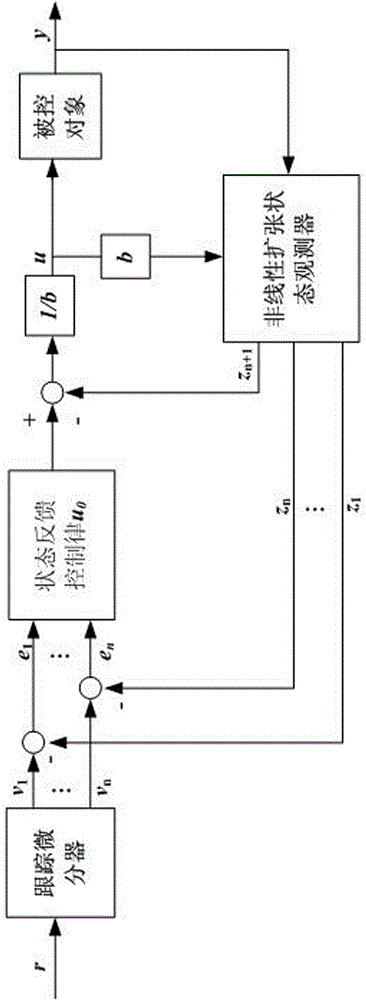
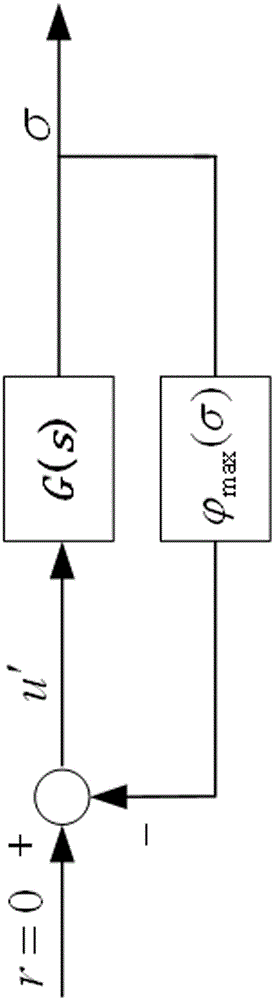
[0110] Combine below Figure 1-Figure 3 And the examples further illustrate the present invention.
[0111] Assuming that the input r of the tracking differentiator in A1 is 0, then the output v of the tracking differentiator is i (i=1, 2, ..., n) are all 0;
[0112] Taking the stability analysis of the second-order nonlinear auto disturbance rejection control system composed of the second-order controlled object and the nonlinear active disturbance rejection controller as an example, the application process of the present invention in practice is explained.
[0113] Stability analysis of nonlinear extended state observer based on Routh criterion.
[0114] Take a second-order linear constant controlled object as an example, its mathematical model is as follows:
[0115] x · 1 = x 2 x · 2 = - 3 x 1 - 5 x 2 + u y = x 1
[0116] (Eq. 29)
[0117] Where x 1 , X 2 Represents the state of the controlled object, Represents the first derivative of the corresponding state, y is the output of the controlled object, and the nonlinear error feedback control law u is the control input of the controlled object.
[0118] Design of nonlinear active disturbance rejection controller:
[0119] In view of the fact that the tracking differentiator is a relatively independent structure, it does not affect the stability of the system, and according to the output v of the tracking differentiator described in hypothesis A1 i (i=1, 2,..., n) are all 0, and no tracking differentiator is designed.
[0120] Since the controlled object is a second-order system, a typical third-order nonlinear extended state observer is designed as follows:
[0121] e = z 1 - y z · 1 = z 2 - β 01 · e z · 2 = z 3 - β 02 · f a l ( e , α 2 , δ ) + b u z · 3 = - β 03 · f a l ( e , α 3 , δ ) (Eq. 30)
[0122] The nonlinear error feedback control law u is designed as follows:
[0123] u=[k 1 fal(v 1 -z 1 , Α′ 1 ,Δ)+k 2 fal(v 2 -z 2 ,α′ 2 ,δ)-z 3 ]/b
[0124] (Eq. 31)
[0125] Here, the output v of the tracking differentiator described in hypothesis A1 i (i = 1, 2, ..., n) are all 0, then v 1 , V 2 All are zero.
[0126] Determine the parameters of the nonlinear active disturbance rejection controller: Let ω o =20, ω c = 10, β 01 =3ω 0 , k 2 = 2ω c , Δ=0.01, α 2 =0.5, α 3 =0.5,α' 1 =0.75,α' 2 = 1.5.
[0127] Stability analysis of nonlinear auto disturbance rejection control system based on robust Popov criterion:
[0128] According to (Equation 17) and (Equation 18), the forward channel transfer function expression of the second-order nonlinear active disturbance rejection control system is obtained:
[0129] G ( s ) = B ‾ 0 s 4 + B ‾ 1 s 3 + B ‾ 2 s 2 + B ‾ 3 s + B ‾ 4 A ~ 0 s 5 + A ~ 1 s 4 + A ~ 2 s 3 + A ~ 3 s 2 + A ~ 4 s + A ~ 5 (Eq. 32)
[0130] The coefficients of the numerator and denominator of (Equation 32) are as follows:
[0131] A ~ 0 = 1 , A ~ 1 = λ 2 , k 2 - a 1 , A ~ 2 = λ 1 k 1 - a 2 - a 1 λ 2 k 2
[0132] A ~ 3 = - a 1 λ 1 k 1 - a 2 λ 2 k 2 , A ~ 4 = - a 2 λ 1 k 1 , A ~ 5 = 0
[0133] B ~ 0 = λ ~ 01 β 01
[0134] B ~ 1 = λ ~ 02 β 02 - a 1 λ ~ 01 β 01 + λ ~ 01 β 01 λ 2 k 2
[0135] B ~ 2 = λ ~ 03 β 03 - a 1 λ ~ 02 β 02 - a 2 λ ~ 01 β 01 + λ ~ 01 β 01 λ 1 k 1 + λ ~ 02 β 02 λ 2 k 2 - a 1 λ ~ 01 β 01 λ 2 k 2
[0136] B ~ 3 = λ ~ 03 β 03 λ 2 k 2 - a 2 λ ~ 02 β 02 + λ ~ 02 β 02 λ 1 k 1 - a 2 λ ~ 01 β 01 λ 2 k 2
[0137] B ~ 4 = λ ~ 03 β 03 λ 1 k 1
[0138] Put ω o =20, ω c = 10, β 01 =3ω 0 , k 2 = 2ω c , Δ=0.01, α 2 =0.5, α 3 =0.5,α' 1 =0.75,α' 2 = 1.5, a 1 =-5, a 2 =-3, set
[0139] e i ∈[0,1](i=1, 2), e∈[0,1], substituting (Equation 32), we can get
[0140] A ~ 0 = 1 , A ~ 1 = [ 7 , 25 ] , A ~ 2 A [ 113 , 419 ] , A ~ 3 A [ 506 , 1640 ] , A ~ 4 A [ 300 , 949 ] , A ~ 05 = 0
[0141] B ~ 0 = A [ 6 , 60 ] , B ~ 1 A [ 282 , 1740 ] , B ~ 2 A [ 3.25 × 10 3 , 3.20 × 10 4 ] ,
[0142] B ~ 3 A [ 2.38 × 10 5 , 2.94 × 10 5 ] , B ~ 4 A [ 8.89 × 10 4 , 2.81 × 10 5 ]
[0143] The 16 transfer functions determined according to the robust Popov criterion are as follows,
[0144] G K = { G ( s ) : G ( s ) } = 60 s 4 + 282 s 3 + 3.25 X 10 3 s 2 + 2.94 X 10 5 s + 2.81 X 10 5 s 5 + 25 s 4 + 113 s 3 + 506 s 2 + 949 s , 60 s 4 + 1740 s 3 + 3.25 X 10 3 s 2 + 2.38 X 10 5 s + 2.81 X 10 5 s 5 + 25 s 4 + 113 s 3 + 506 s 2 + 949 s , 6 s 4 + 1740 s 3 + 3.20 X 10 4 s 2 + 2.38 X 10 5 s + 8.89 X 10 4 s 5 + 25 s 4 + 113 s 3 + 506 s 2 + 949 s , 6 s 4 + 282 s 3 + 3.20 X 10 4 s 2 + 2.94 X 10 5 s + 8.89 X 10 4 s 5 + 25 s 4 + 113 s 3 + 506 s 2 + 949 s , 60 s 4 + 1740 s 3 + 3.25 X 10 3 s 2 + 2.38 X 10 5 s + 2.81 X 10 5 s 5 + 25 s 4 + 419 s 3 + 506 s 2 + 300 s , 60 s 4 + 282 s 3 + 3.25 X 10 3 s 2 + 2.94 X 10 5 s + 2.81 X 10 5 s 5 + 25 s 4 + 419 s 3 + 506 s 2 + 300 s , 6 s 4 + 1740 s 3 + 3.20 X 10 4 s 2 + 2.38 X 10 5 s + 8.89 X 10 4 s 5 + 25 s 4 + 419 s 3 + 506 s 2 + 300 s , 6 s 4 + 282 s 3 + 3.20 X 10 4 s 2 + 2.94 X 10 5 s + 8.89 X 10 4 s 5 + 25 s 4 + 419 s 3 + 506 s 2 + 300 s ,
[0145] 6 s 4 + 1740 s 3 + 3.20 × 10 4 s 2 + 2.38 × 10 5 s + 8.89 × 10 4 s 5 + 7 s 4 + 419 s 3 + 1640 s 2 + 300 s , 60 s 4 + 282 s 3 + 3.25 × 10 3 s 2 + 2.94 × 10 5 s + 2.81 × 10 5 s 5 + 7 s 4 + 419 s 3 + 1640 s 2 + 300 s , 60 s 4 + 1740 s 3 + 3.25 × 10 3 s 2 + 2.38 × 10 5 s + 2.81 × 10 5 s 5 + 7 s 4 + 419 s 3 + 1640 s 2 + 300 s , 6 s 4 + 282 s 3 + 3.20 × 10 4 s 2 + 2.94 × 10 5 s + 8.89 × 10 4 s 5 + 7 s 4 + 419 s 3 + 1640 s 2 + 300 s , 6 s 4 + 282 s 3 + 3.20 X 10 4 s 2 + 2.94 X 10 5 s + 8.89 X 10 4 s 5 + 7 s 4 + 506 s 3 + 1640 s 2 + 949 s , 60 s 4 + 282 s 3 + 3.25 X 10 3 s 2 + 2.94 X 10 5 s + 2.81 X 10 5 s 5 + 7 s 4 + 506 s 3 + 1640 s 2 + 949 s , 60 s 4 + 1740 s 3 + 3.25 X 10 3 s 2 + 2.38 X 10 5 s + 2.81 X 10 5 s 5 + 7 s 4 + 506 s 3 + 1640 s 2 + 949 s , 6 s 4 + 1740 s 3 + 3.20 X 10 4 s 2 + 2.38 X 10 5 s + 8.89 × 10 4 s 5 + 7 s 4 + 506 s 3 + 1640 s 2 + 949 s }
[0146] (Eq. 33)
[0147] Then according to (Equation 33), the corresponding Popov curve is drawn as image 3 Shown. by image 3 It can be seen that all the Popov curves satisfy the Popov criterion, so the system is stable.
[0148] Stability analysis of nonlinear extended state observer based on Routh criterion:
[0149] Due to α 2 =α 3 , Therefore (Equation 28) is established, namely
[0150] β 01 β 02β 03 (Eq. 34)
[0151] Therefore, the nonlinear extended state observer represented by (Equation 30) is stable.
[0152] The above-mentioned embodiments are only preferred embodiments of the present invention, rather than exhaustive lists of possible embodiments of the present invention. For those of ordinary skill in the art, any obvious changes made to the present invention without departing from the principle and spirit of the present invention should be deemed to be included in the protection scope of the present invention.
