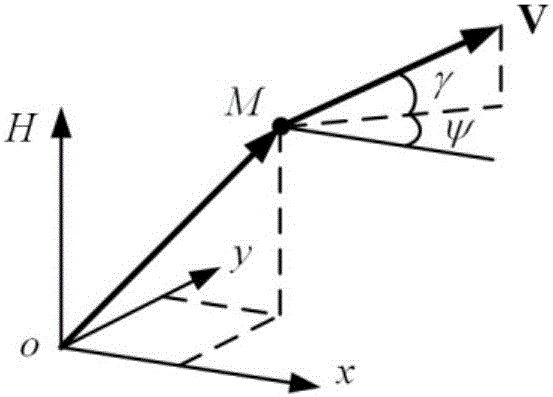
Explicit guidance law for rocket with terminal speed, trajectory inclination angle and overload constraint

A technology of ballistic inclination and guidance law, applied in the field of explicit guidance law, which can solve the problem of increasing the amount of misses

Inactive Publication Date: 2017-06-13
BEIHANG UNIV
View PDF0 Cites 21 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At the same time, the traditional explicit guidance law cannot satisfy the constraints on terminal velocity, ballistic inclination

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Explicit guidance law for rocket with terminal speed, trajectory inclination angle and overload constraint
  • Explicit guidance law for rocket with terminal speed, trajectory inclination angle and overload constraint
  • Explicit guidance law for rocket with terminal speed, trajectory inclination angle and overload constraint

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

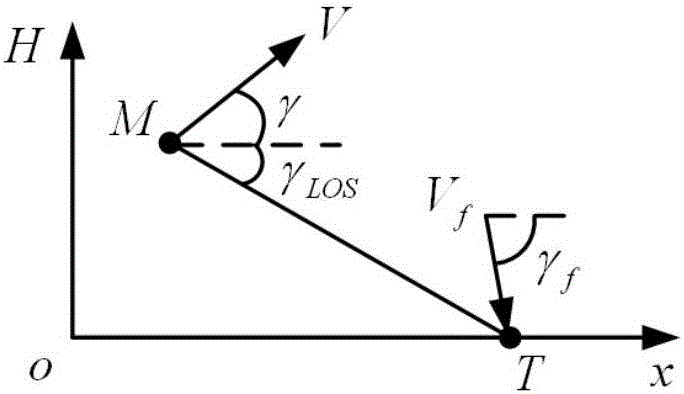
[0351] In this embodiment, the influence of gravity is ignored, and the aircraft performs deceleration and glide movement: V(t)=1000-5t(m / s), and it is hoped that the aircraft will hit the target with a ballistic inclination angle of 0deg. The initial condition of the aircraft is: x 0 =0km,H 0 =10km,γ 0 =0deg, the initial condition of the target is: x T =50km,H T = 0 km.

[0352] By assuming γ-γ LOS ≈0 get, Solve the expression of remaining flight distance with respect to time By solving the equation R(t f )=0 to obtain the terminal time t f value. Set the values ​​of the characteristic roots to be λ 1 =-2,λ 2 =-2.5, then equation (32) can be solved to obtain the guidance law coefficient C 1 =10.5,C 2 =-5. At this point, the analytical form of the ballistic shaping guidance law of the present invention can be obtained as

[0353]

[0354] As a comparison, the traditional ballistic shaping guidance law has a constant velocity and a linear motion equation i...

Embodiment 2

[0359] This embodiment is consistent with the initial conditions of Embodiment 1, and the characteristic value is set to λ 1 =-2+2i,λ 2 =-2-2i. The available guidance law coefficient is C 1 =13,C 2 =-8, then the analytical form of the ballistic shaping guidance law of the present invention is

[0360]

[0361] The analytical form of the traditional ballistic shaping guidance law is

[0362]

[0363] Fig. 4 (a) shows the ballistic curve under the action of the ballistic shaping guidance law of the present invention, and Fig. 4 (b) shows the acceleration time curve of the ballistic shaping guidance law of the present invention and the traditional ballistic shaping guidance law and numerical simulation comparison. The results show that the ballistic shaping guidance law of the present invention has a high degree of approximation to the nonlinear model, which proves that the acceleration command does have oscillations, but the acceleration tends to zero when approaching ...

Embodiment 3

[0365] This embodiment is consistent with the initial conditions of Embodiment 1, and the characteristic value is set to λ 1 =λ 2 =-2, then the guidance law coefficient can be obtained as C 1 =9,C 2 =-4, then the analytical form of the ballistic shaping guidance law of the present invention is

[0366]

[0367] The analytical form of the traditional ballistic shaping guidance law is

[0368]

[0369] Fig. 5(a) shows the ballistic curve under the action of the ballistic shaping guidance law of the present invention, and Fig. 5 (b) shows the acceleration time curve of the guidance law of the present invention compared with the traditional ballistic shaping guidance law and numerical simulation. The results show that in this case, the ballistic shaping guidance law of the present invention can highly approximate the numerical simulation results of the nonlinear model, and can control the moment when the aircraft hits the target, and the ballistic inclination angle and ac...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The present invention provides an explicit guidance law for a rocket with a terminal speed, a trajectory inclination angle and overload constraint. The explicit guidance law for a rocket is formed by integration of an optimal trajectory-shaping guidance law and a terminal speed control scheme. The optimal trajectory-shaping guidance law can control an aircraft to hit a target from a predetermined direction, the terminal speed control scheme controls the transverse maneuverable accelerated speed of the aircraft bending so as to control the prolonging of flight distance to regulate the size of the terminal speed, and the size of the transverse maneuverable accelerated speed is determined through an iteration correction algorithm. The analysis guidance law can satisfy the terminal trajectory inclination angle and the terminal speed constraint, and allow an aircraft to approach to the maneuverable accelerated speed of the target to gradually decrease to 0; further, the present invention provides a method for determination of coefficients of guidance law for a rocket, namely the coefficients of guidance law for a rocket are determined through proper selection of features of a linear approximation system; and moreover, a coefficient stability domain of the guidance law for the rocket is obtained so as to strictly prove that only if the coefficients of guidance law for a rocket are in the stability domain the guiding system is stable and the aircraft hits a target at a small angle of attack.

Description

technical field [0001] The invention relates to an explicit guidance law with terminal velocity, ballistic inclination and overload constraints, and belongs to the fields of aerospace technology, weapon technology and guidance control. Background technique [0002] For the terminal flight of a hypersonic gliding vehicle, it is generally hoped to guide the vehicle to hit the ground target from an approximately vertical direction, so that the seeker has a better field of view; at the same time, it is necessary to control the terminal speed of the vehicle, because in general Excessive terminal velocity is not conducive to ensuring heat flux density and incoming flow pressure constraints, and too small terminal velocity is not conducive to the need for penetration. If the aircraft is loaded with a ground-penetrating warhead, it is required to hit the target with a smaller angle of attack; otherwise, when it hits the target with a larger angle of attack, the projectile body will ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G05D1/10
CPCG05D1/107
Inventor 陈万春余文斌赵鹏雷
Owner BEIHANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap