Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A method of encoding and decoding of digital fountain code based on arm

An implementation method, digital fountain technology, applied in the field of encoding and decoding of digital fountain codes, can solve the problems of high decoding cost, complex calculation, and many iterations, so as to reduce the number of iterations, simplify the calculation process, and reduce the number of iterations Effect

Active Publication Date: 2020-05-26
HARBIN INST OF TECH
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0010] The purpose of the present invention is to solve the problems of repeated selection in the existing digital fountain code LRLTC algorithm, large decoding overhead, large number of iterations, and complex calculations, and propose a method for implementing encoding and decoding of digital fountain codes based on ARM

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A method of encoding and decoding of digital fountain code based on arm
  • A method of encoding and decoding of digital fountain code based on arm
  • A method of encoding and decoding of digital fountain code based on arm

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0035] Specific implementation mode one: a kind of coding and decoding implementation method of the digital fountain code based on ARM of the present embodiment specific process is:

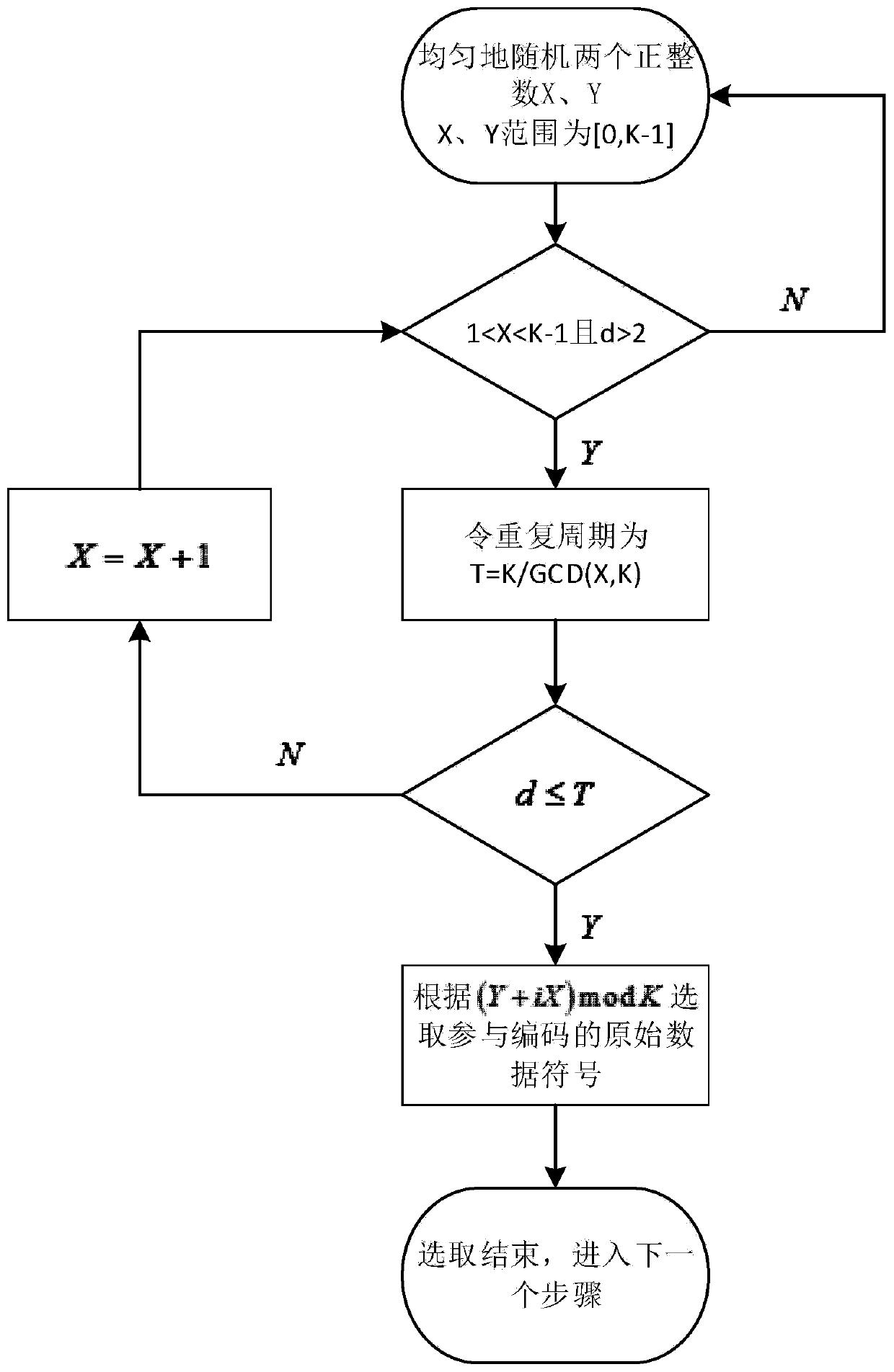
[0036] Step 1. Uniformly and randomly generate two positive integers X and Y in the encoding module, where X and Y are independent of each other and satisfy: 1≤X≤K-1, 1≤Y≤K-1;

[0037] K is the number of original data packets, and the value of K is a positive integer;

[0038] The robust solitary wave distribution is:

[0039] In the formula, ρ(i) is the ideal solitary wave distribution function; τ(i) is the variable in the robust solitary wave distribution formula;

[0040]

[0041] Where 1≤j≤K; sum is the summation function;

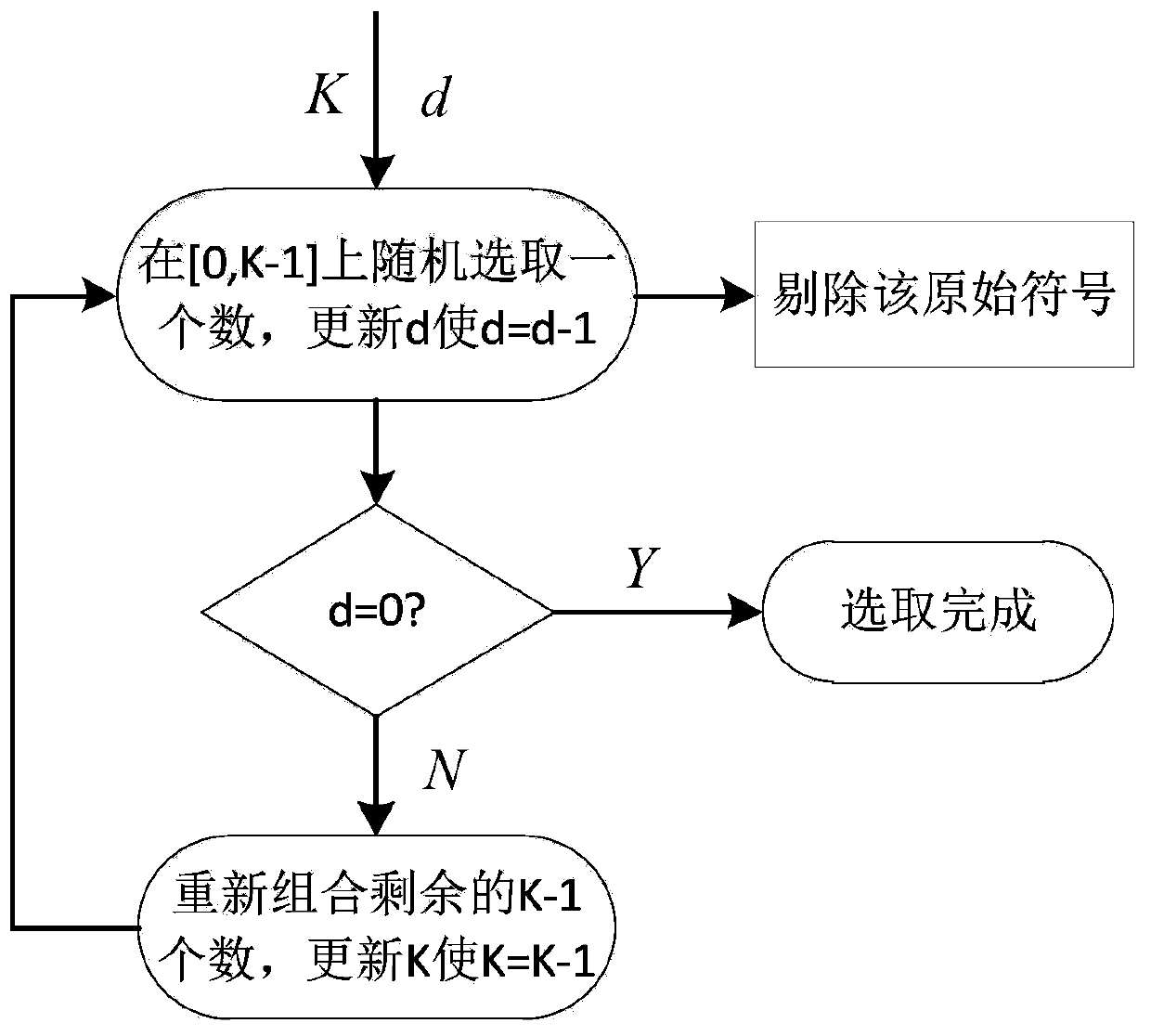
[0042] Randomly select a parameter r between 0-1, there must be a j in 1≤j≤k so that sum(j)

[0043] Step 2. If the positive integer X and the degree value d do not satisfy the condition 1

specific Embodiment approach 2

[0080] Specific embodiment two: the difference between this embodiment and specific embodiment three is: the ideal solitary wave distribution function ρ(i) is:

[0081]

[0082] Other steps and parameters are the same as those in the first embodiment.

specific Embodiment approach 3

[0083] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is: the variable τ(i) in the robust solitary wave distribution formula is:

[0084]

[0085] where s is the mathematical expectation of encoded N packets of degree 1, c is a free variable, and δ is the probability limit that the decoding module cannot decode after receiving the encoded N data packets;

[0086] N is the number of encoded data packets, K≤N.

[0087] Other steps and parameters are the same as those in Embodiment 1 or 2.

[0088] Specific Embodiment 3: This embodiment differs from one of Specific Embodiments 1 to 3 in that: the value of c is 1.

[0089] Other steps and parameters are the same as those in the first to third specific embodiments.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a digital fountain code encoding and decoding method based on ARM. The invention relates to a digital fountain code encoding and decoding method. The problems of repeated selection, large decoding cost, large number of iterations and complicated calculation of the existing digital fountain code LRLTC algorithm are solved. The method comprises the steps that two positive integers are generated randomly and uniformly; sum (j) is acquired according to a robust solitary wave distribution formula; a parameter is randomly selected between 0 and 1, so that sum(j)<r<sum(j+1) and d=j; if X and d satisfy the condition that 1<X<K-1 and d is equal to or greater than 3, the period length in which d is repeated is T; if d is equal to or less than T, d is not repeatedly selected; each original data packet participating in encoding is numbered; according to d, the numbered original data packet is selected for encoding; and the encoded original data packet is transmitted to a decoding module for decoding, so as to realize encoding and decoding. The method provided by the invention is used in the field of channel encoding.

Description

technical field [0001] The invention relates to a coding and decoding realization method of a digital fountain code. Background technique [0002] In this highly informationized society, information and communication are already the lifeblood of modern society: rapid economic development, social progress and other fields are inseparable from the development of communication technology. The main criteria for judging the quality of a communication system are reliability and effectiveness. It can be seen that a good digital communication system requires a high degree of reliability in the communication process, that is, the bit error rate must be low enough; however, some errors will inevitably occur during signal transmission, that is, bit errors. In order to avoid or reduce these errors, an error control (Error Control) technology is subsequently produced to ensure reliable transmission of data in a digital communication system. [0003] Digital fountain code is a forward e...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L1/00
CPCH04L1/0057
Inventor 王振永李杰马铭徐誉师鹏程朱洪涛
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com