Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Rounding Error Compensation Method for S-curve Acceleration and Deceleration

A technology of error compensation, acceleration and deceleration, applied in the field of motion control of numerical control system

Active Publication Date: 2019-03-08
SHANDONG UNIV
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The invention proposes an S-curve acceleration and deceleration error compensation method, which can accurately solve the rounding error, realize theoretical no difference, and eliminate the speed fluctuation problem caused by the rounding error

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Rounding Error Compensation Method for S-curve Acceleration and Deceleration
  • A Rounding Error Compensation Method for S-curve Acceleration and Deceleration
  • A Rounding Error Compensation Method for S-curve Acceleration and Deceleration

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0057] The proof of principle of the program of the present invention is as follows:

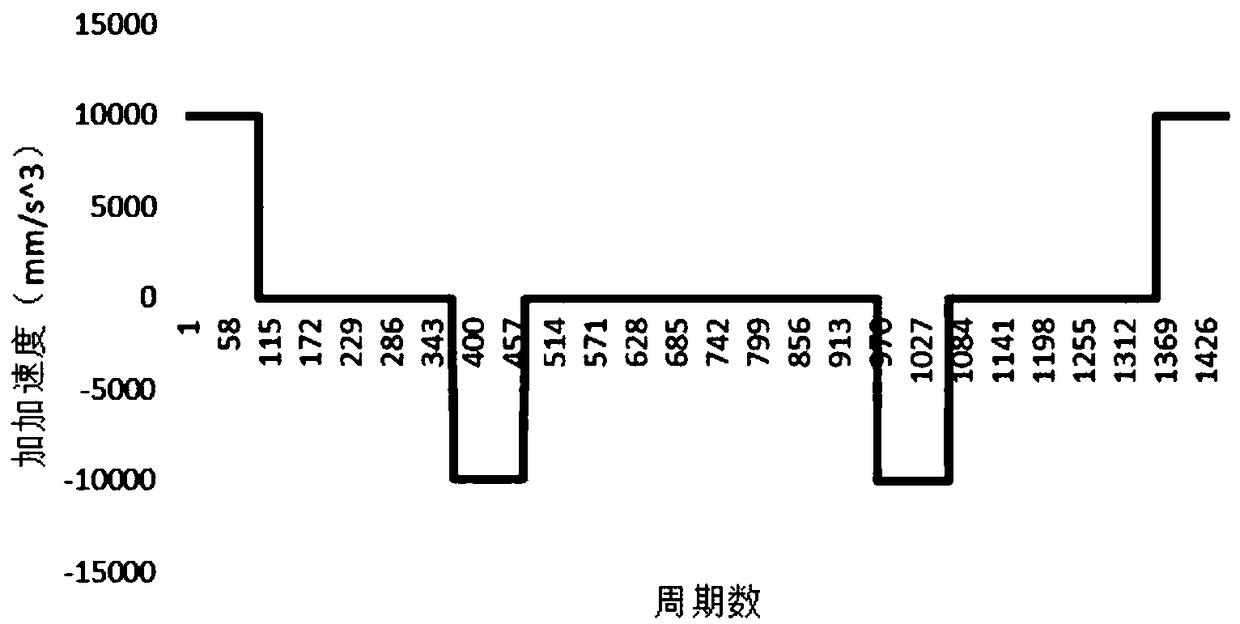
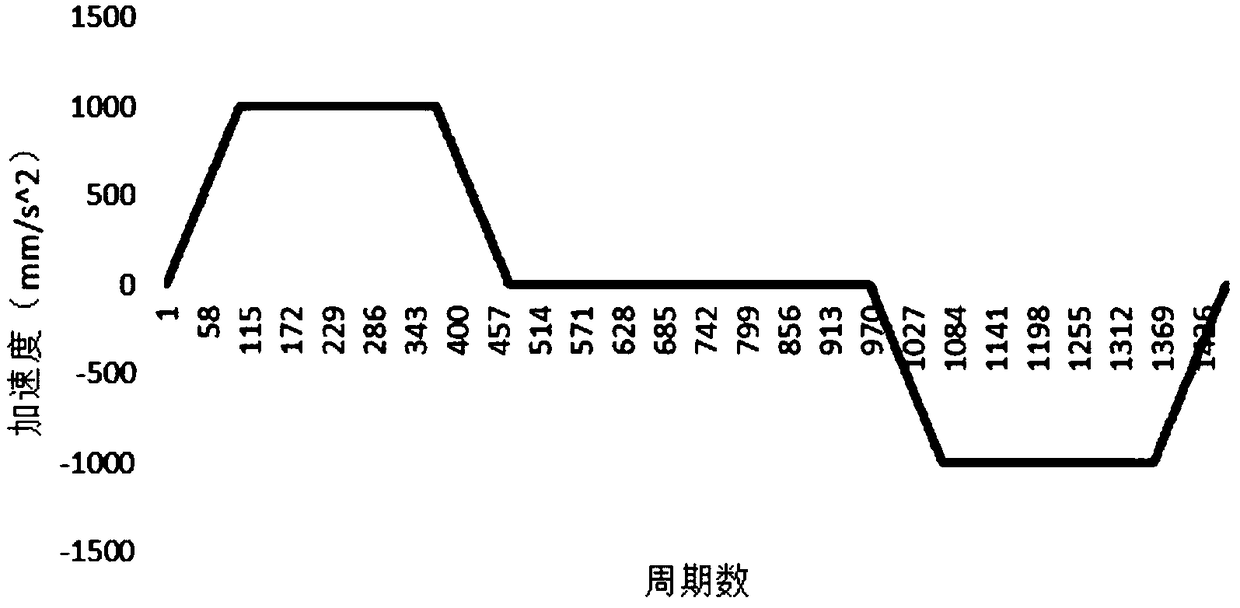
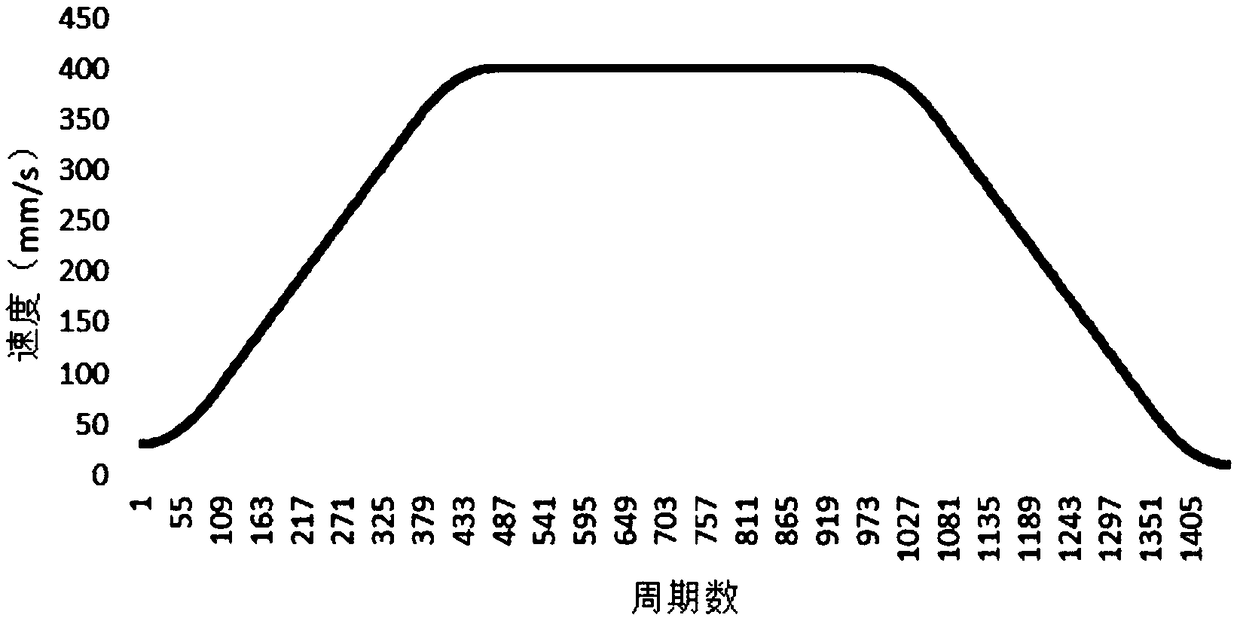
[0058] In the S-curve acceleration and deceleration, the jerk of each segment is constant and discontinuous, and the jerk of the uniform acceleration segment and the uniform deceleration segment is 0, but it may not be 0 after parameter adjustment, so the jerk of each segment is respectively J 1 、J 2 、J 3 , J 5 , J 6 , J 7 , a i (i=1,2,...,7) for t i The acceleration value at the moment, v i for t i The speed value at the moment, ΔS i is the displacement in the i-th section, according to the nature of S-curve acceleration and deceleration, there is J 1 =J com , J 2 =0,J 3 =J com J 5 =J com , J 6 =0,J 7 =J com , Δt 1 =Δt 3 , Δt 5 =Δt 7 ;

[0059] The integral relationship between jerk and acceleration, velocity and displacement is:

[0060]

[0061] where τ i =t-t i-1 (i=1,2,...,7; t 0 = 0);

[0062] There are the following relations:

[0063] a 1 =J 1 Δt ...

Embodiment 2

[0368] A rounding error compensation method for S-curve acceleration and deceleration, the method steps are as described in Embodiment 1, the difference is that in this example, set: S=200mm, v s =30mm / s, v e = 10mm / s, v com =400mm / s, a com =1000mm / s^2, J com =10000mm / s^3, T s =0.001s

[0369] First, the original 7-segment time and displacement are planned according to the S-curve acceleration and deceleration algorithm, among which:

[0370] t1=0.1s, t2=0.26833s, t3=0.1s, t4=0s, t5=0.1s, t6=0.28833s, t7=0.1s;

[0371] s1=4.66667mm; s2=57.467mm; s3=38.1664mm; s4=0mm, s5=38.1664mm; s6=58.867mm; s7=2.66667mm;

[0372] It is not difficult to see that the total planning time T=t1+t2+t3+t4+t5+t6+t7=0.95666s is not an integer multiple of the interpolation cycle.

[0373] If T=t acc1 +t con +t dec1 = m 1 T s +Δt, where m1 is a non-negative integer, then Δt=0.00066s, in order to ensure that the total planning time T is an integer multiple of the interpolation period, Δt ne...

Embodiment 3

[0384] A rounding error compensation method for S-curve acceleration and deceleration, the method steps are as described in Embodiment 1, the difference is that in this example, set: S=201.6mm, v s =30mm / s, v e = 10mm / s, v com =400mm / s, a com =1000mm / s^2, J com =10000mm / s^3, T s =0.001s

[0385] First, the original 7-segment time and displacement are planned according to the S-curve acceleration and deceleration algorithm, among which:

[0386] t1=0.1s, t2=0.27s, t3=0.1s, t4=0.00025s, t5=0.1s, t6=0.29s, t7=0.1s;

[0387] s1=4.66667mm; s2=58.05mm; s3=38.3333mm; s4=0.1mm, s5=38.3333mm; s6=59.45mm; s7=2.66667mm;

[0388] It is not difficult to see that the total planning time T = t1 + t2 + t3 + t4 + t5 + t6 + t7 = 0.96025s, which is not an integer multiple of the interpolation period.

[0389] If T=t acc1 +t con +t dec1 = m 1 T s +Δt, where m1 is a non-negative integer, then Δt=0.00025s, in order to ensure that the total planning time T is an integer multiple of the i...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the field of motion control of numerical control systems and specifically relates to a rounding error compensation method for S-curve acceleration and deceleration. After primary S curve planning, an acceleration segment, a constant-speed segment and a deceleration segment cannot exist at the same time. Different error compensation strategies need to be adopted aiming at different combination types according to analysis on above motion parameter relation. When the constant-speed segment is in presence, a displacement adjustment method is selected. When the constant-speed segment is in absence while the acceleration segment and the deceleration segment are in presence at the same time, a maximal speed adjustment method is selected. When the constant-speed segment isin presence and the displacement of the constant-speed segment is comparatively short and cannot meet adjustment requirements, displacement adjustment is employed first and then speed adjustment is employed. According to the invention, single-segment interpolation time is not adjusted and the interpolation total time is adjusted only. Interpolation time of compensation is reduced as far as possible, so that the interpolation efficiency is improved. Based on the adjusted interpolation time, all motion parameters are calculated again by using the displacement and speed adjustment methods, so that a condition that the motion parameters do not surpass limits after adjustment is ensured.

Description

technical field [0001] The invention belongs to the field of motion control of a numerical control system, in particular to a rounding error compensation method for S-curve acceleration and deceleration. Background technique [0002] In the numerical control system, in order to avoid the impact, out of step, overtravel and oscillation of each axis, and to ensure the stable and accurate positioning of the moving parts, acceleration and deceleration control must be carried out. At the same time, good acceleration and deceleration control can realize the rapid response of the CNC machine tool, reach the specified speed in a short time, shorten the acceleration and deceleration time, and improve production efficiency. Commonly used acceleration and deceleration control methods include linear acceleration and deceleration, exponential acceleration and deceleration, and S-curve acceleration and deceleration. Although linear acceleration and deceleration and exponential accelerati...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B19/404
CPCG05B19/404G05B2219/35408
Inventor 张承瑞倪鹤鹏陈齐志张岳姬帅胡天亮
Owner SHANDONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com