Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Emergency material storage site selection optimizing method based on box uncertainty set

A technology of emergency materials and optimization methods, applied in biological models, data processing applications, instruments, etc., can solve problems such as the accurate demand for emergency materials, traffic roads are damaged and uncertain, and achieve scientific site selection, good robustness, The effect of improving efficiency

Active Publication Date: 2018-03-30
LIAONING TECHNICAL UNIVERSITY
View PDF10 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, site selection decisions are often affected by uncertain factors. Whether a potential disaster occurs, where it occurs, and the type and level of the disaster are unknown. Therefore, the exact demand for emergency supplies and the destruction of traffic roads are uncertain.
Therefore, the main difficulty in location decision-making lies in how to deal with the uncertainty brought about by the weight change of demand points

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Emergency material storage site selection optimizing method based on box uncertainty set
  • Emergency material storage site selection optimizing method based on box uncertainty set
  • Emergency material storage site selection optimizing method based on box uncertainty set

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

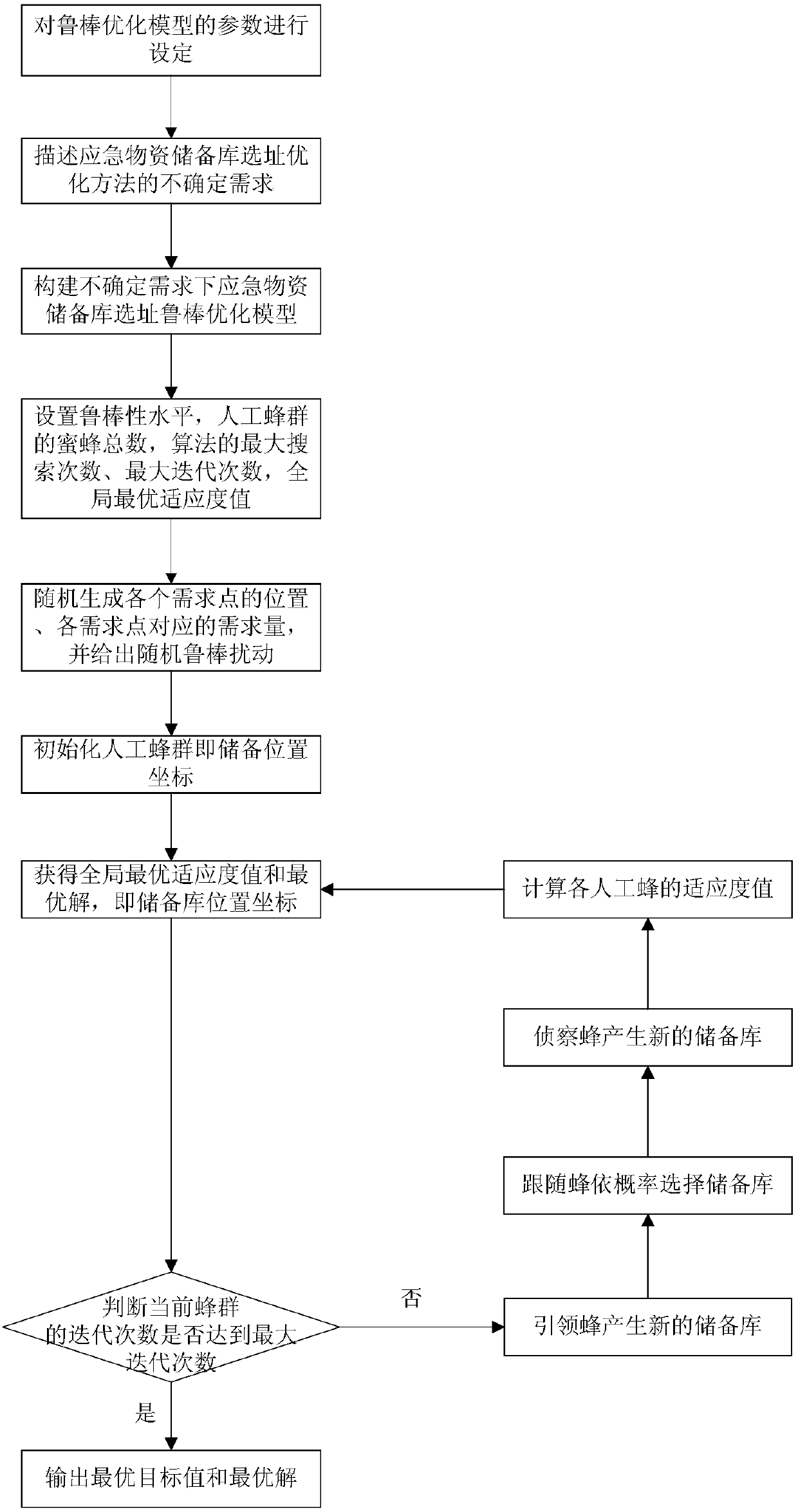
[0047] An optimization method for site selection of emergency material reserve based on uncertain set of boxes, the process is as follows figure 1 As shown, the specific method is as follows:

[0048] Step 1: Set the parameters of the robust optimization model, including the number m of emergency material reserves to be built, the total number n of demand points, and the set of demand points P={P 1 ,P 2 ,...,P n}, the set of demands of demand points W={w 1 ,w 2 ,...,w n}, the demand w of the jth demand point j and w j >0, the average value of demand at the jth demand point Uncertain demand at the jth demand point The emergency material quantity w provided by the i-th emergency material reserve to the j-th demand point ij and w ij >0, the coordinate P of the jth demand point j :( j ,b j ) and P j ∈P, the coordinate X of the i-th emergency material reserve i :(x i ,y i ), the capacity s of the i-th emergency material reserve i , the distance d(X i ,P j ), t...

Embodiment 2

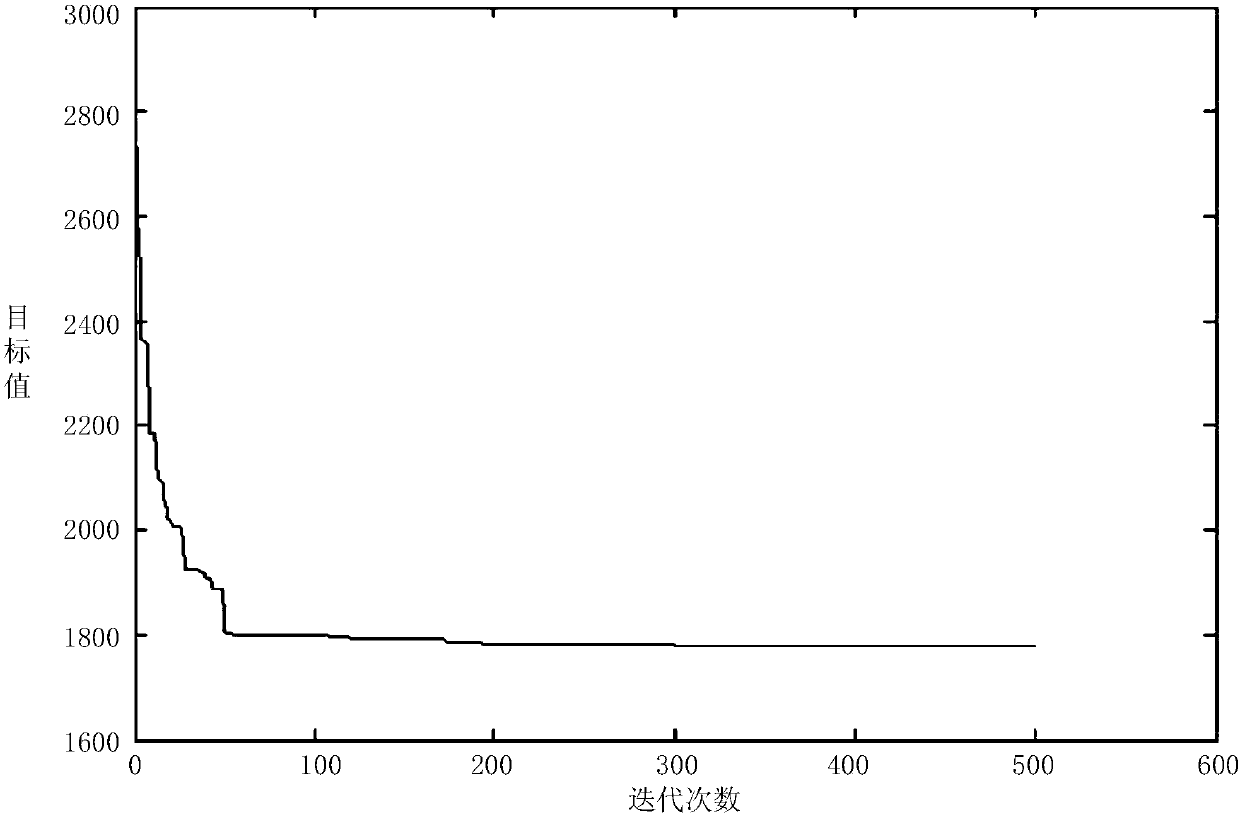
[0094] In this embodiment, randomly scattered demand points m=100, the proposed emergency material reserve n=8, the demand of demand points is randomly generated within [0,50], and the starting point coordinates of the site selection area are (0, 0), the coordinates of the end point of the site selection area are (1000, 1000), given the box constraints Set the uncertain demand disturbance δ∈[0,10], and use the method of optimizing the location of the emergency material reserve based on the uncertain set of boxes to conduct experiments on the location selection model of the large-scale reserve. The parameter settings and specific implementation steps are the same as in Example 1. .

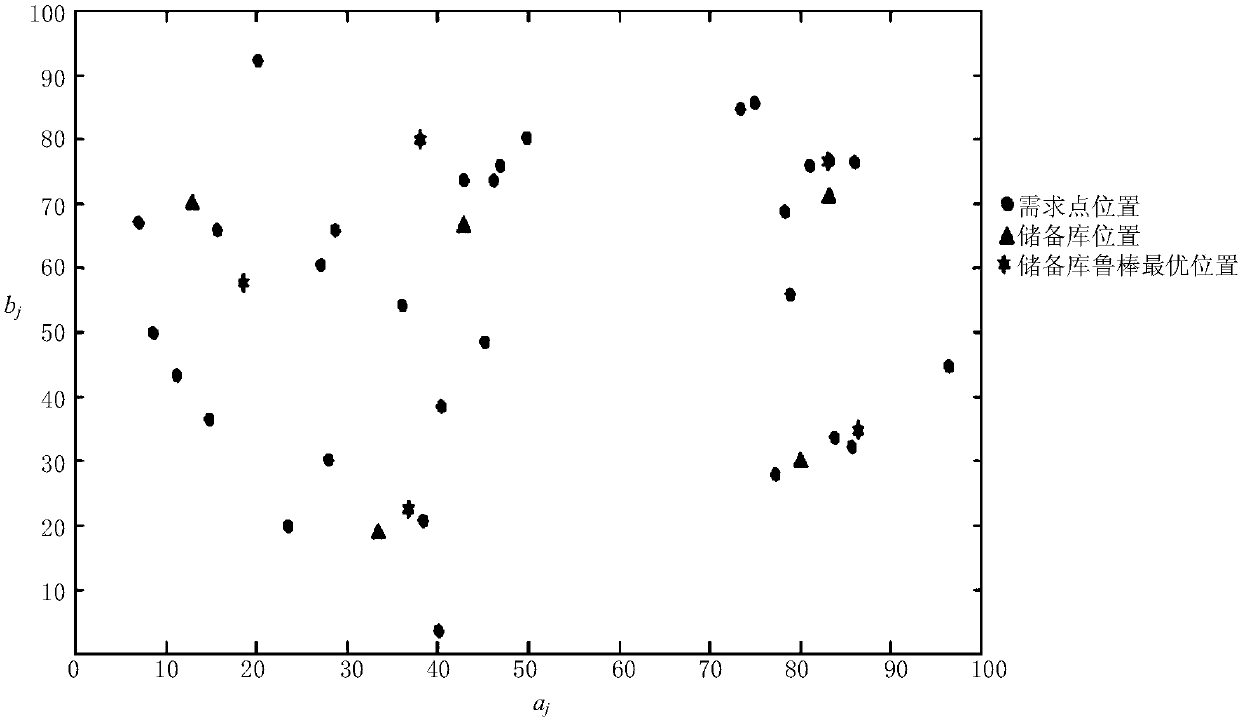
[0095] In Example 2 of the present invention, among the 100 demand points, the optimal location and the robust optimal location of the 8 emergency material storage warehouses are as follows: Figure 4 and shown in Table 3.

[0096] Table 3 Optimal solution coordinates and robust optimal solution...

Embodiment 3

[0102] In this embodiment, the emergency material reserve to be established is n=10, and the demand of the demand point is randomly generated within [0,100] and remains unchanged. The parameter setting and specific implementation steps are the same as in Embodiment 1, and different disturbances are given respectively. Level δ 1 ∈[0,10], δ 2 ∈[10,100].

[0103] In Example 3 of the present invention, there are 100 demand points and 10 emergency material reserves, and the optimal location and robust optimal location of the scientific location under the disturbance level [0,10] are as follows Figure 6 (a) shown.

[0104] In Example 3 of the present invention, there are 100 demand points and 10 emergency material reserves, and the optimal location and robust optimal location of the scientific location under the disturbance level [10,100] are as follows Figure 6 (b) shown.

[0105] In Example 3 of the present invention, when there are 100 demand points and 10 emergency materia...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an emergency material storage site selection optimizing method based on a box uncertainty set, and relates to the technical field of the emergency service facility site selection optimization in the uncertain environment. The method comprises the following steps: setting parameters of a robust optimization model and uncertain demand of a method thereof; constructing the robust optimization model; randomly generating the position of each demand point and the corresponding demand quantity thereof, and providing random robust disturbance; to obtain a global optimum fitnessvalue and an optimal solution, namely emergency material storage position coordinates. According to the provided emergency material storage site selection optimizing method based on the box uncertainty set, because the model has the non-convex, non-linear and multi-constraint features, and has the NP-hard feature mathematically, a coding method of an artificial bee colony algorithm is designed forsolving the robust optimization model, the robustness is good in the different scales and the different disturbance demands, the scientific site selection of the emergency material storage in uncertain factors is realized, and a risk is avoided in the greatest degree under the uncertain situation.

Description

technical field [0001] The invention belongs to the technical field of site selection optimization for emergency service facilities in an uncertain environment, and in particular relates to a method for site selection optimization of an emergency material reserve based on an uncertain set of boxes. Background technique [0002] In recent years, natural disasters, accident disasters and various sudden disasters have occurred frequently, the scope of influence has been expanding, and the degree of impact has been deepening, posing a major threat to human survival and social development. Emergency material reserves are the material basis for effectively responding to and overcoming sudden disasters. Once a sudden disaster occurs, the demand for emergency materials will expand rapidly in a short period of time. Therefore, the strategic reserve of some necessary disaster relief materials is the key to improving the efficiency of emergency rescue. The emergency material reserve i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06Q10/04G06Q50/26G06N3/00
CPCG06N3/006G06Q10/04G06Q50/26
Inventor 于冬梅高雷阜赵世杰
Owner LIAONING TECHNICAL UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com