Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Porous material structure having three-dimensional negative Poisson's ratio

A technology of negative Poisson's ratio and porous materials, applied in the field of porous material structures with three-dimensional negative Poisson's ratio, can solve the problems of limited types, small selection of engineering applications, and difficult manufacturing process, so as to increase the selection and facilitate Design analysis, achieve isotropic effect

Inactive Publication Date: 2018-08-14
SUN YAT SEN UNIV
View PDF4 Cites 18 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] However, the types of existing three-dimensional negative Poisson's ratio materials are limited, the manufacturing process is difficult, and there are few options for engineering applications. Therefore, it is of great theoretical and practical significance to design new three-dimensional negative Poisson's ratio materials.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Porous material structure having three-dimensional negative Poisson's ratio
  • Porous material structure having three-dimensional negative Poisson's ratio
  • Porous material structure having three-dimensional negative Poisson's ratio

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

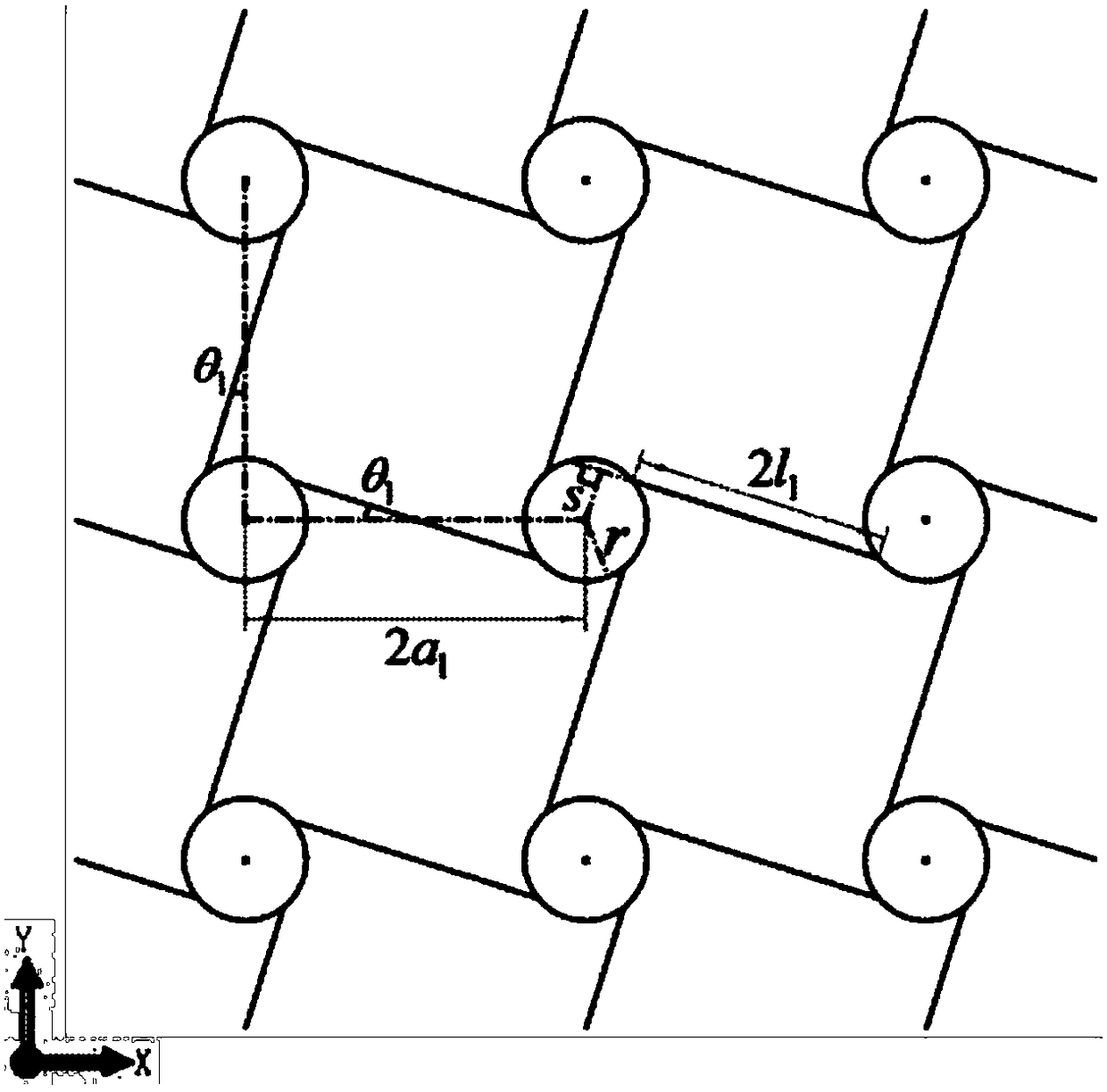
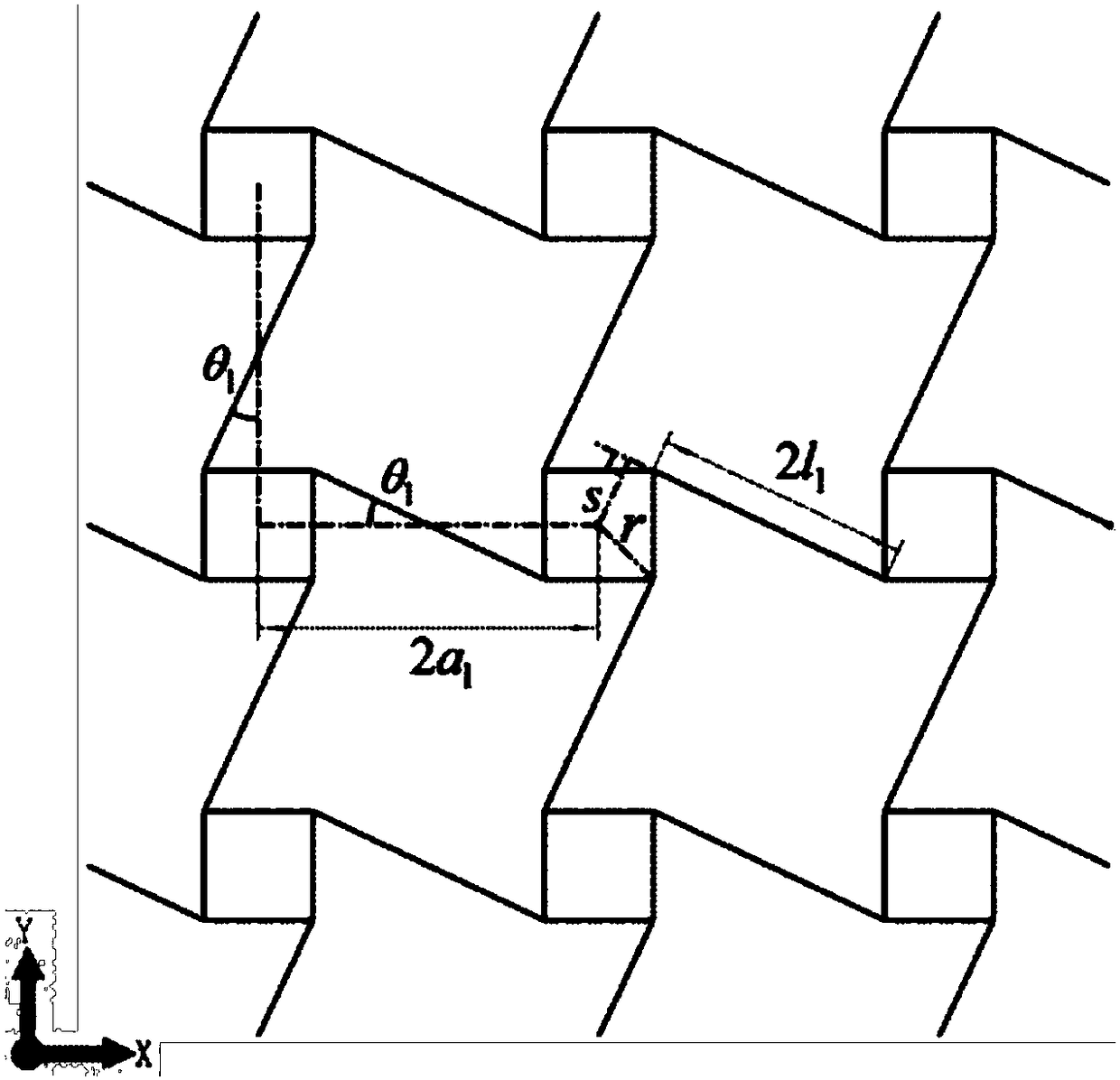
[0044] Such as figure 1 As shown, in a porous material structure with a three-dimensional negative Poisson’s ratio provided by this embodiment, the support unit is in the shape of a ring; in each layer of network structure, the centroids of all support units are uniform on the XOY plane Distributed and arranged into a regular quadrilateral network topology, the centroid of each support unit is located at the node of the network topology. That is, the supporting units are arranged in a square array along the X-axis and the Y-axis, and the distance between every two adjacent supporting units in the directions of the X-axis and the Y-axis is equal, so that the centroids of every four adjacent supporting units form a square.

[0045]Four connecting ligaments are uniformly distributed around each supporting unit along the circumferential direction, and each supporting unit is respectively connected to other four supporting units adjacent to it on the X-axis and Y-axis through the f...

Embodiment 2

[0052] Such as Figure 5 As shown, in a porous material structure with a three-dimensional negative Poisson’s ratio provided by this embodiment, the support unit is in the shape of a ring; in each layer of network structure, the centroids of all support units are uniform on the XOY plane Distributed and arranged in a regular triangular network topology, that is, on the XOY plane, the distance between every three adjacent support units is equal, so that the centroids of every three adjacent support units form an equilateral triangle.

[0053] Six connecting ligaments are uniformly distributed around each supporting unit along the circumferential direction, and each supporting unit is respectively connected to other six supporting units adjacent to it on the XOY plane through the six connecting ligaments. The six connecting ligaments on each supporting unit are rotationally symmetrical about the centroid of the supporting unit; that is, the geometric position of any connecting l...

Embodiment 3

[0058] Such as Figure 6 As shown, in a porous material structure with a three-dimensional negative Poisson's ratio provided by the present invention, the support unit is in the shape of a ring; in each network structure, the centroids of all support units are evenly distributed on the XOY plane Arranged in a regular hexagonal network topology array, that is, on the XOY plane, the centroids of every six support units form a regular hexagon, and the centroids of each support unit are located at the vertices of the regular hexagon, so that the support unit The distribution on the XOY plane is honeycomb;

[0059] Three connecting ligaments are uniformly distributed around each supporting unit along the circumferential direction, and each supporting unit is respectively connected to other three supporting units adjacent to it on the XOY plane through the three connecting ligaments. The three connecting ligaments on each supporting unit are rotationally symmetrical about the centr...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a porous material structure having a three-dimensional negative Poisson's ratio. The porous material structure comprises a plurality of net structures which are sequentially stacked in parallel along a Z-axis direction, and the upper net structure and the lower net structure which are adjacent are connected by a support ligament, wherein net structure extends along an XOY plane. The porous material structure having the three-dimensional negative Poisson's ratio eliminates the tensile-shear coupling effect of the two-dimensional substructure of the XOY plane during deformation, so the three-dimensional structure constitutive relationship usually is orthotropic, and can be easily designed and analyzed. Geometrical dimensions are adjusted to make the structure isotropicand greatly change the negative Poisson's ratio values in all three directions, so the choice of practical applications is increased.

Description

technical field [0001] The invention relates to the field of porous material structures, in particular to a porous material structure with three-dimensional negative Poisson's ratio. Background technique [0002] Negative Poisson's ratio material, also known as auxetic material, refers to a material that expands (or shrinks) perpendicular to the loading direction when it is stretched (or compressed) in one direction. Due to the unique properties different from ordinary materials, negative Poisson's ratio materials have advantages that other materials cannot match in many aspects, especially the physical and mechanical properties of materials have been greatly improved, such as the shear modulus of materials can be improved. Weight, fracture resistance, indentation resistance, and negative Poisson's ratio materials can also achieve excellent sound absorption performance and impact resistance. [0003] However, the types of existing three-dimensional negative Poisson's ratio ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): B32B3/12B32B7/08
CPCB32B3/12B32B7/08
Inventor 富明慧刘凤鸣胡玲玲
Owner SUN YAT SEN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com