Robust Estimation Method of Power Flow Jacobian Matrix in Smart Distribution Network Considering Sparsity
A technology for intelligent distribution network and robust estimation, which is applied to AC networks, circuit devices, AC network circuits with the same frequency from different sources, etc. Contains bad data and other problems to avoid adverse effects, improve robustness, and achieve the effect of robust estimation
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
specific example
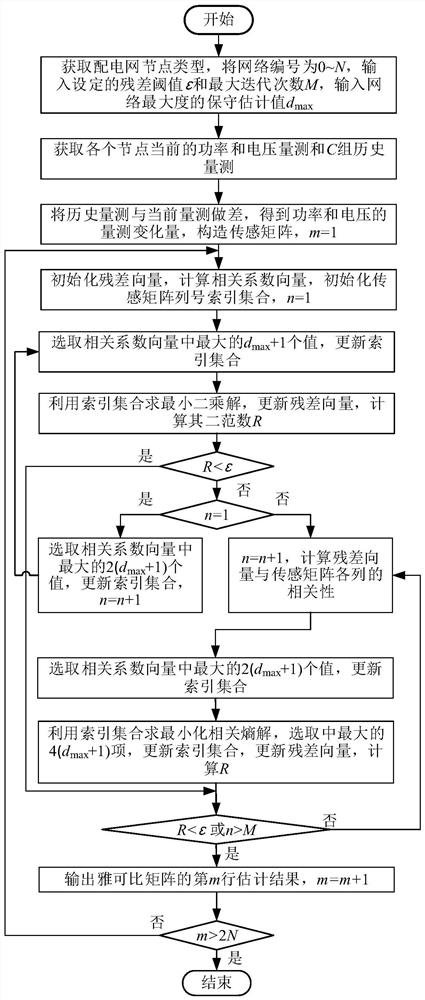
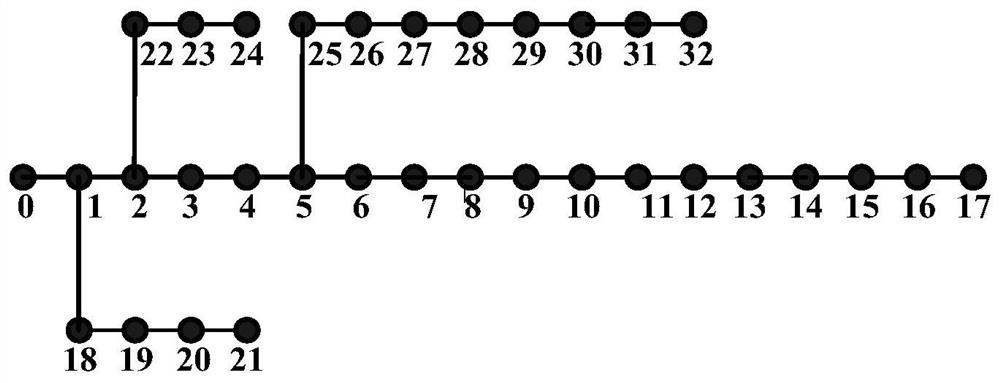
[0117] First, input the IEEE33 node calculation example network topology connection relationship such as figure 2 As shown in , node 0 is the balance node, and other nodes 1 to 32 are PQ nodes. The system's reference capacity is 1MVA, and the reference voltage is 12.66kV. The current power measurement of each PQ node is shown in Table 1. The conservative estimate of the maximum degree of the input network is 4, the standard deviation of the simulated measurement power variation and error random number is set to 0.01 and 0.025%, respectively, and the number of measurement groups is set to 30, 35, 40, 45, 50, 55 , 60. Calculate the errors of the Jacobian matrix and the voltage power sensitivity matrix using the following formula.
[0118]
[0119] In the formula, denote the estimated values of the elements of the Jacobian matrix, J i,j is the theoretical value of the elements of the Jacobian matrix.
[0120] Use the following formula to calculate the estimation error ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com