[0052] The present invention will be further described below in conjunction with the drawings.
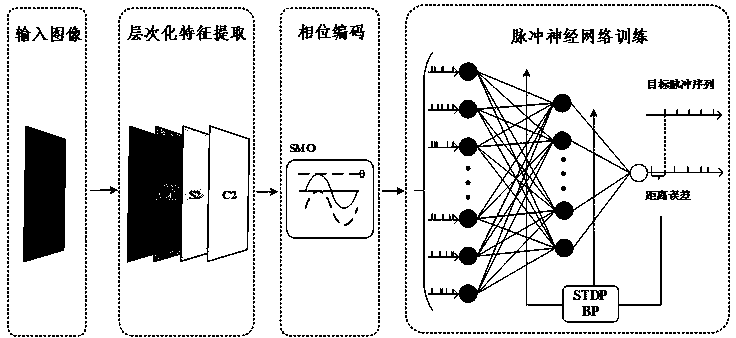
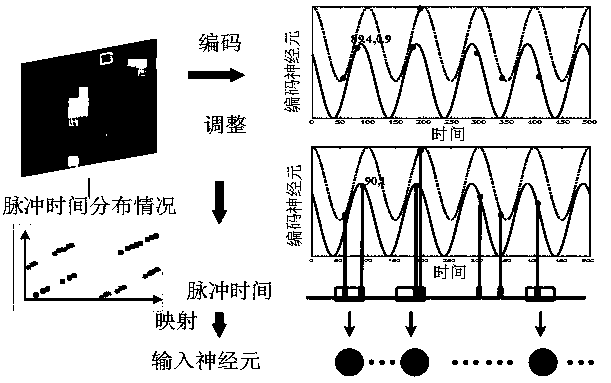
[0053] Figure 1 to Figure 4 Each stage of the entire image recognition process is shown separately. The process can be divided into 3 steps. The specific content is as follows:
[0054] Step 1 Hierarchical feature extraction
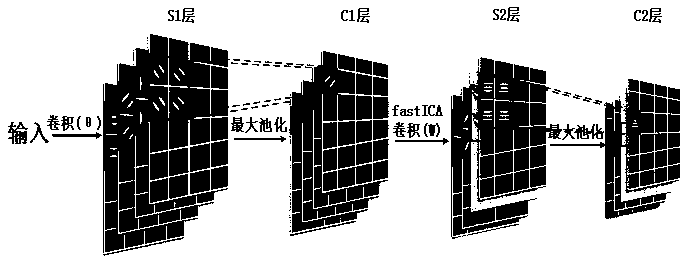
[0055] among them figure 2 Describes the overall process of hierarchical feature extraction. A four-layer model is used in this process, namely S1 layer, C1 layer, S2 layer and C2 layer. The parameter values involved here are mainly for the MNIST data set. The specific operations of each layer are as follows:
[0056] 1.1S1 layer: Gabor filtering to extract edge information
[0057] Cells in the primary visual cortex are strongly sensitive to edge information, and the frequency and direction expression of the Gabor filter is considered to be similar to that of the human visual system, so in this step two-dimensional Gabor filter is used to simulate the receptive field of simple cells . The input image is filtered by a Gabor filter bank of 4 directions and 2 scales, and 8 response maps are obtained. The kernel function of Gabor filtering used is:
[0058]
[0059] s.t.x 0 =x cosθ+y sinθ
[0060] and y 0 =-x sinθ+y cosθ
[0061] Where λ is the wavelength, σ is the phase shift, and γ is the aspect ratio, with values of 3.5, 0.3, and 0.8λ respectively. θ represents the direction. The four directions selected in the present invention are (0°, 45°, 90°, 135°), and the two scales (filter size) selected are 5×5 and 7×7, respectively.
[0062] 1.2C1 layer: Max-Pooling operation
[0063] After the edge information is selected through the S1 layer, two scales and four directions of response maps are obtained. The C1 layer first uses Max-Pooling to take the maximum value of each pixel on the response map with different scales in the same direction, that is, the maximum value in the sense of "adjacent scales". On this result, according to the size of the sliding window, the maximum value of the response in the window is taken, that is, the maximum value in the sense of "spatially adjacent", where each movement of the window has 1/2 window overlap. Through the combination of the S1 layer and the C1 layer, a selective and invariant response is obtained, and the purpose of data dimensionality reduction is achieved at the same time.
[0064] 1.3 S2 layer: use FastICA autonomous learning features
[0065] The operation of FastICA is used in the S2 layer because it not only satisfies the sparsity but also can learn features independently, and can be well combined with the manual features of the S1 layer. In sparse coding, the cost function is
[0066] SC=AS
[0067]
[0068]
[0069] According to the FastICA algorithm, the cost function is converted to
[0070]
[0071] The FastICA algorithm iteratively finds a set of W values, and arranges the basis vectors in W from large to small according to requirements. In the present invention, the first 6 basis vectors are selected as feature templates to process the C1 result, and finally each result of C1 obtains corresponding 6 response graphs.
[0072] 1.4 C2 layer: Max-Pooling
[0073] The operation of the C2 layer is similar to the operation of the C1 layer. The 6 response images obtained from the S2 layer are spliced into a large image. On this large image, the maximum value of the spatially adjacent pixels in the sliding window is calculated. The sliding window used in the C2 layer The windows do not overlap during the sliding process.
[0074] Step 2 Use pulse coding to convert pixel information into time information
[0075] The coding strategy uses two types of coding neurons, which are excitatory coding neurons and inhibitory coding neurons. According to the pixel value information and the corresponding position information, the pixel is determined to be in the activated state or the inhibited state. Each pixel corresponds to an encoding neuron, and the pixel information is encoded into corresponding time information according to certain rules. This rule involves three steps, which are encoding on the periodic oscillation function, fine-tuning the time information to a multiple of t_step, and mapping the time information to the input neuron according to a certain rule, so that each input neuron corresponds to a pulse sequence. The specific process is as follows
[0076] step1: x i ∈j th encoding neuron
[0077] step2:if t i t max
[0078] t i = T i -t max
[0079] step3:
[0080] Where t max =500ms, t_setp=1ms, n=2, Input neurons=220.
[0081] Step 3 Use multi-layer pulse neural network for training and learning
[0082] In order to improve the classification performance of the spiking neural network, the present invention selects a multi-layer learning algorithm. The algorithm constructs the functions of input layer-hidden layer and hidden layer-output layer in a probabilistic way:
[0083]
[0084]
[0085] Set the threshold voltage V in this method thr =15mV, the change of reset voltage is V each time a pulse is generated rest =-15mV, set the escape rate of different layers to Δu h =0.5mV, Δu o = 5mV. The membrane time constant and the synaptic time constant are set to 10 and 5, respectively. A randomly generated Poisson pulse sequence is used to verify the performance of the algorithm, and the results are as follows Figure 4 Shown. It can be seen that the originally scattered pulses can gradually generate pulses around the set target pulse sequence after training and learning of the hidden layer and the output layer. In the final classification judgment, the vRD (van Rossum Distance) index is used to judge the distance between the actual output pulse sequence and the target pulse sequence, and the smaller distance is selected as the corresponding category. The brief algorithm description is as follows:
[0086]
[0087] STDP calculates the weight change based on the error between the actual output pulse and the target pulse. According to the back propagation method, after calculating the weight change of the output layer, the hidden layer can also be changed accordingly. In step2, the Adam algorithm is used to adjust the learning rate. From the figure 3(d), it can be seen that after adjusting the learning rate, the actual output pulse sequence is closer to the target pulse sequence.
