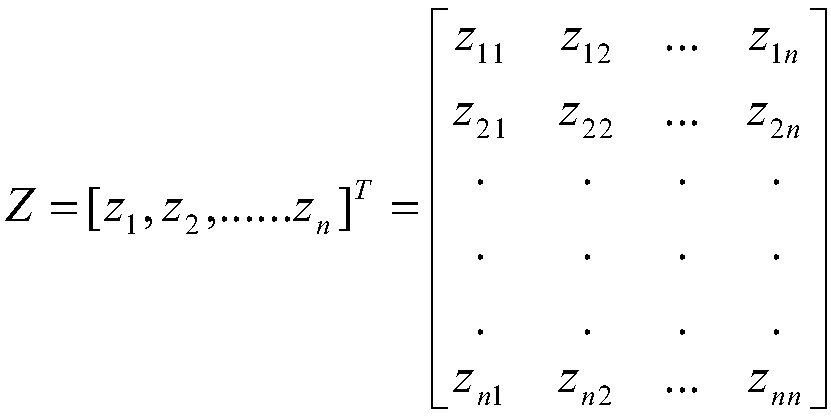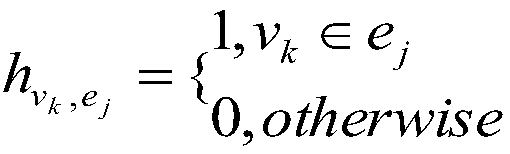Multi-modal data analysis method and system based on high Laplacian regularization and low-rank representation
A low-rank representation and data analysis technology, applied in character and pattern recognition, medical automated diagnosis, instruments, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
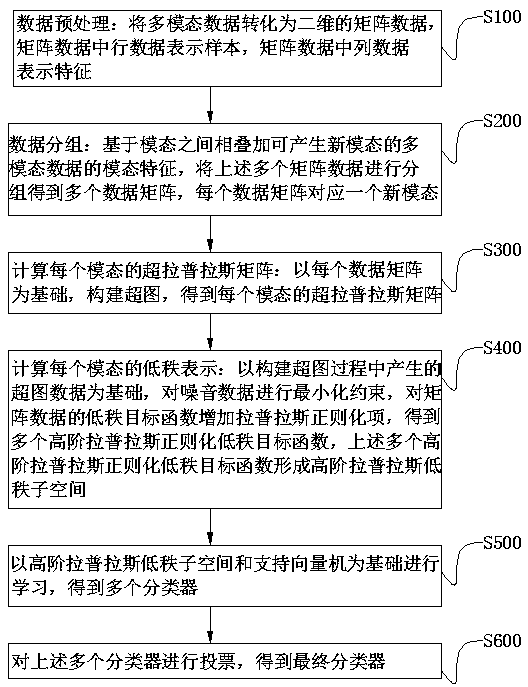
[0062] as attached figure 1 As shown, the multimodal data classification method of high Laplacian regularization and low rank representation of the present invention combines low rank representation and Laplacian regularization term to construct non-negative sparse super Laplacian regularization low rank representation model, and apply the non-negative sparse super-Laplacian regularized low-rank representation model to multimodal data analysis, including the following steps:
[0063] Step S100, data preprocessing: converting the multimodal data into two-dimensional matrix data, the row data in the matrix data represent samples, and the column data in the matrix data represent features;
[0064] Step S200, data grouping: based on the modal characteristics of multimodal data that can generate new modalities by superimposing the modalities, group the above-mentioned multiple matrix data to obtain multiple data matrices, each data matrix corresponds to a new modal state;
[0065...
Embodiment 2
[0102] In this embodiment, the multimodal data analysis system of high Laplacian regularization and low-rank representation includes:
[0103] The data processing module is used to perform data processing on multimodal data to obtain multiple data matrices, each data matrix corresponds to a modality, and the data in each data matrix is two-dimensional matrix data;
[0104] The data analysis module is used to combine the low-rank representation and the graph Laplacian regularization term to construct a non-negative sparse super-Laplacian regularization low-rank representation model, and through the non-negative sparse super-Laplacian regularization term Learn each data matrix to obtain a high-order Laplacian low-rank subspace;
[0105] A classification module for learning based on high-order Laplacian low-rank subspaces and support vector machines to obtain multiple classifiers;
[0106] The voting module is used to vote for the above multiple classifiers to obtain the final...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com