Empirical wavelet transform method for determining sub-band boundary by using kurtosis spectrum
A technique of determining the sub-band and kurtosis spectrum, applied in the field of signal processing, it can solve the problems such as the loss of rationality of the wavelet sub-band boundary, the influence of the peak distribution of the signal, and the lack of validity of the signal component.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
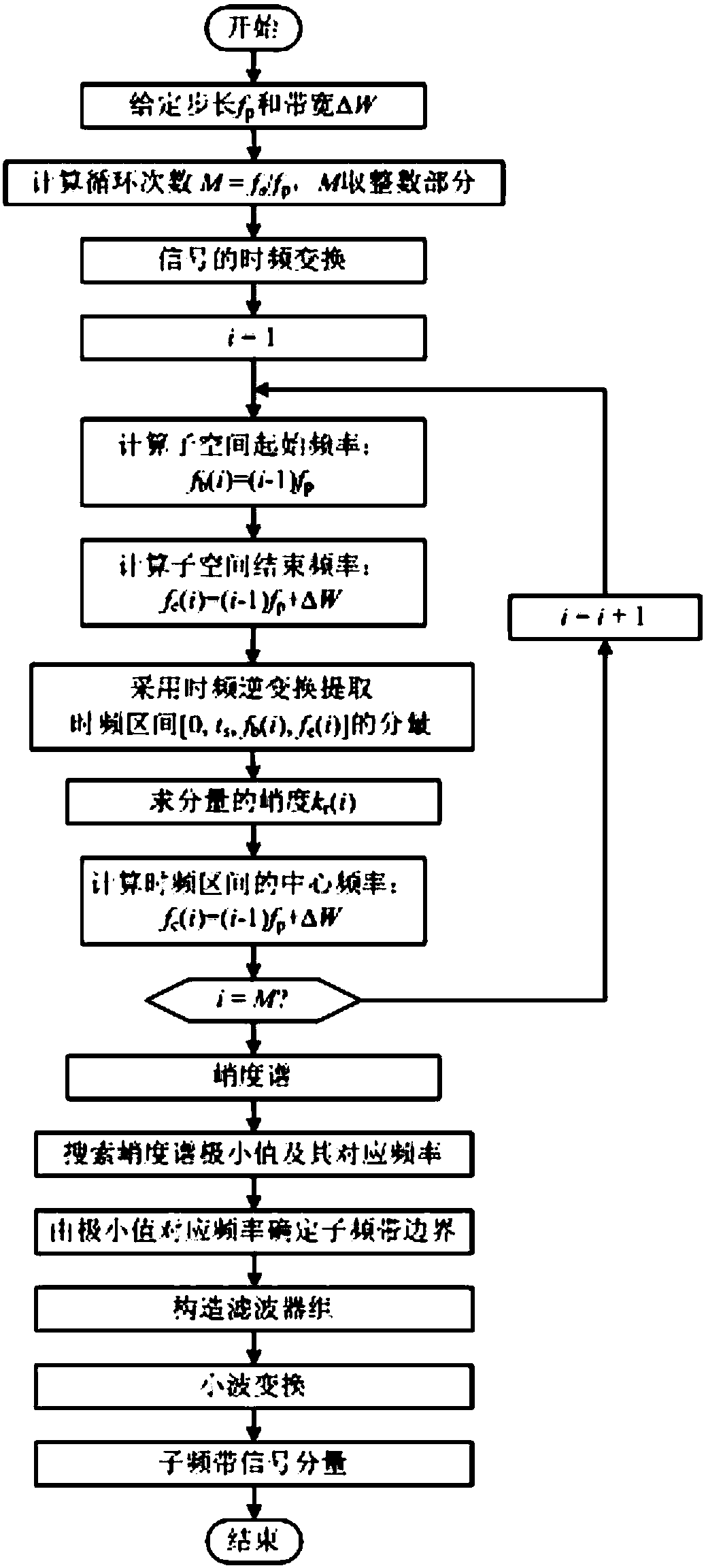
[0022] This embodiment provides an empirical wavelet transform method that uses kurtosis spectrum to determine the boundary of a subband, which is implemented in the following steps:
[0023] 1) The signal is first time-frequency transformed, and then based on the time-frequency transformation result, along the frequency axis of the time-frequency transformation result, with a fixed frequency step and a fixed bandwidth, the local time-frequency region is sequentially inversely transformed to obtain The kurtosis of the signal component in the time-frequency region is calculated, and the kurtosis sequence is finally obtained;
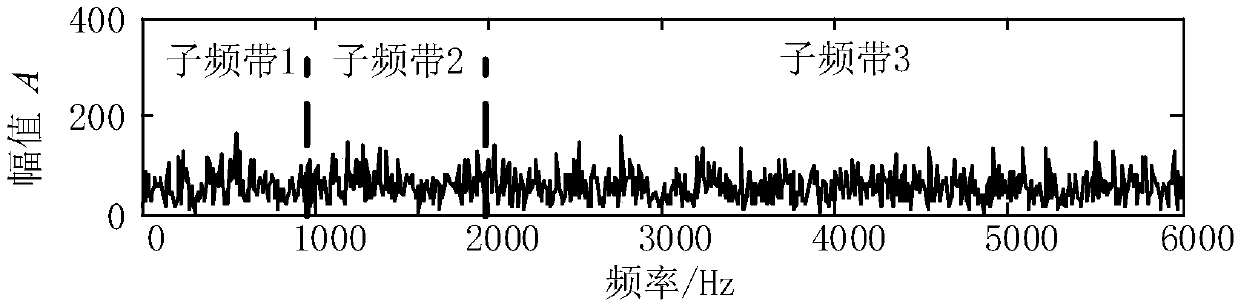
[0024] 2) Taking the center frequency of each local time-frequency region as the abscissa and the kurtosis of its signal components as the ordinate, the kurtosis spectrum of the signal can be obtained;
[0025] 3) Find the local minimum on the kurtosis spectrum, and arrange the corresponding frequencies from small to large. These frequencies are the wavelet subb...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com