MEMS gyroscope noise estimation and filtering method
A noise estimation and noise technology, applied in gyro effect for speed measurement, gyroscope/steering sensing equipment, calculation, etc., can solve problems such as large error, difficult to realize, and complex calculation
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
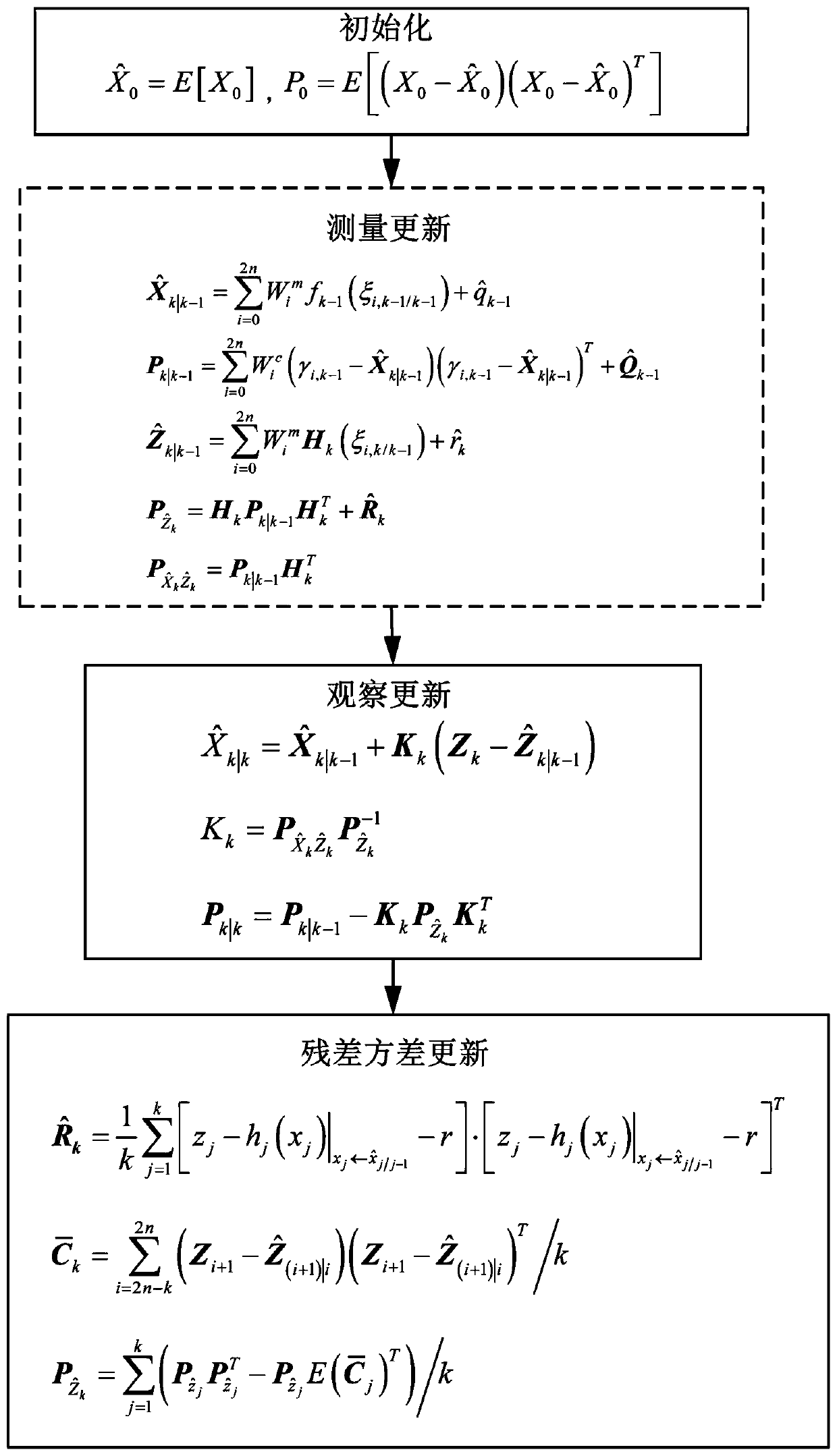
[0081] Such as figure 1 As shown, the embodiment of the present invention provides a MEMS gyro noise estimation and filtering method, including:
[0082] Step 1. Obtain a signal with noise, preset the system characteristic function and initialize it;
[0083]
[0084] is the prior mean value of the initial state X0, and P0 is the covariance matrix;
[0085] Step 2. Calculate the Sigma point and construct the statistical characteristic coefficient at the same time:
[0086]
[0087] Among them, a ∈ R represents the adjustment coefficient, usually a small positive value; Represents the matrix nP k-1 The i-th column of the root mean square; the weight ω i for:
[0088]
[0089] Step 3. Measure and update the one-step state prediction mean value, error covariance matrix, forecast mean value and covariance matrix:
[0090] Sigma point ξ constructed according to step 2 i,k-1 / k-1 Through the nonlinear state function f k ( )+q spread as γ i,k / k-1 , by γ i,k / k-1 T...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com