Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

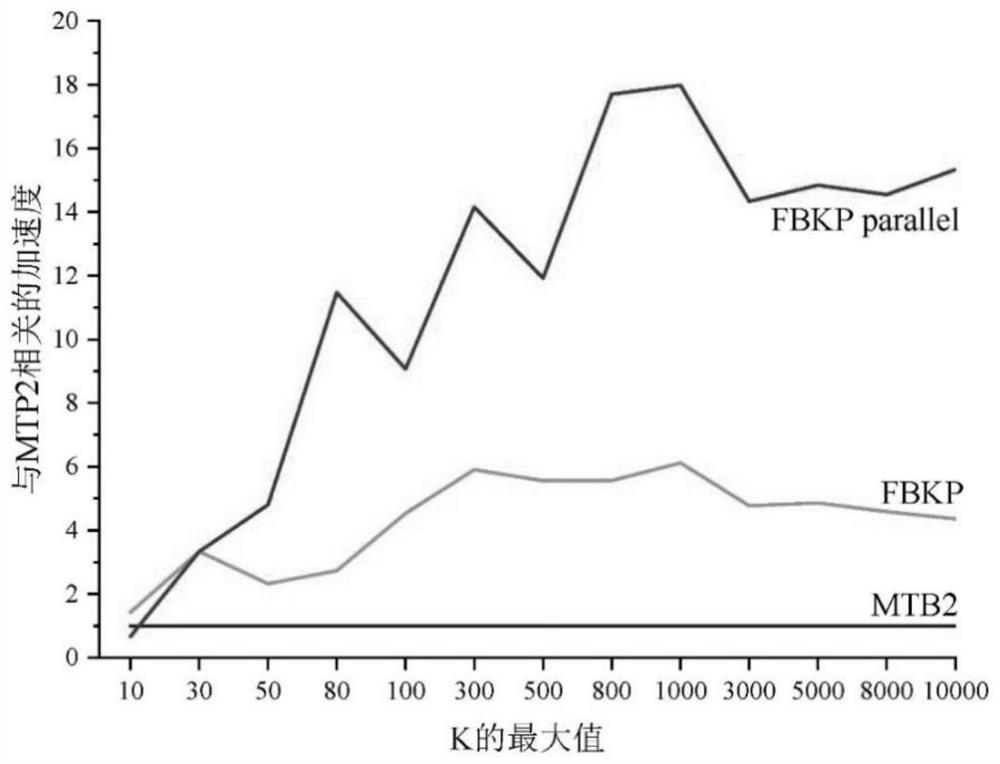
Method for solving bounded knapsack problem based on improved dynamic programming algorithm

A technology of dynamic programming algorithm and knapsack problem, which is applied in computing, complex mathematical operations, data processing applications, etc., can solve the problems of increasing algorithm time and space complexity, not taking into account the same value and weight, etc., to reduce redundancy More calculations, fast solution, good efficiency effect

Pending Publication Date: 2021-01-12
HUNAN UNIV OF TECH
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

These two methods convert BKP into 0-1 KP solution without considering that the items in BKP have the same value and weight, which will generate a lot of unnecessary redundant calculations and increase the time and space complexity of the algorithm

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for solving bounded knapsack problem based on improved dynamic programming algorithm
  • Method for solving bounded knapsack problem based on improved dynamic programming algorithm
  • Method for solving bounded knapsack problem based on improved dynamic programming algorithm

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

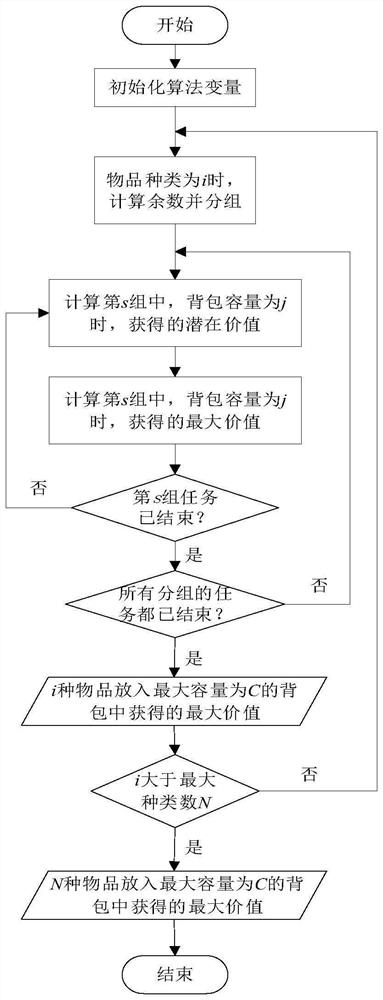
[0040] A method for solving the bounded knapsack problem based on an improved dynamic programming algorithm (hereinafter referred to as FBKP), which defines the maximum number of items as N, the maximum capacity of the knapsack as C, the item type as i, 0≤i≤N, and each item A single value of v i , with weight w i , the number of each item is k i ;Define a (N+1)×(C+1) two-dimensional value table f, the knapsack capacity is j, 0≤j≤C; f i (j) indicates the maximum value of putting i items into the knapsack when the capacity is j. When i=0 or j=0, the maximum value obtained is f (i＝0) (j) and f (j＝0) (i) are all 0.

[0041] Calculate the remainder a, group the capacity states j according to the capacity remainder a, and put the capacity states j with the same capacity remainder into a group for calculation. This embodiment is sequential calculation, so the first group of calculations ends before the next group starts .

[0042] Such as figure 1 As shown, the above method in...

Embodiment 2

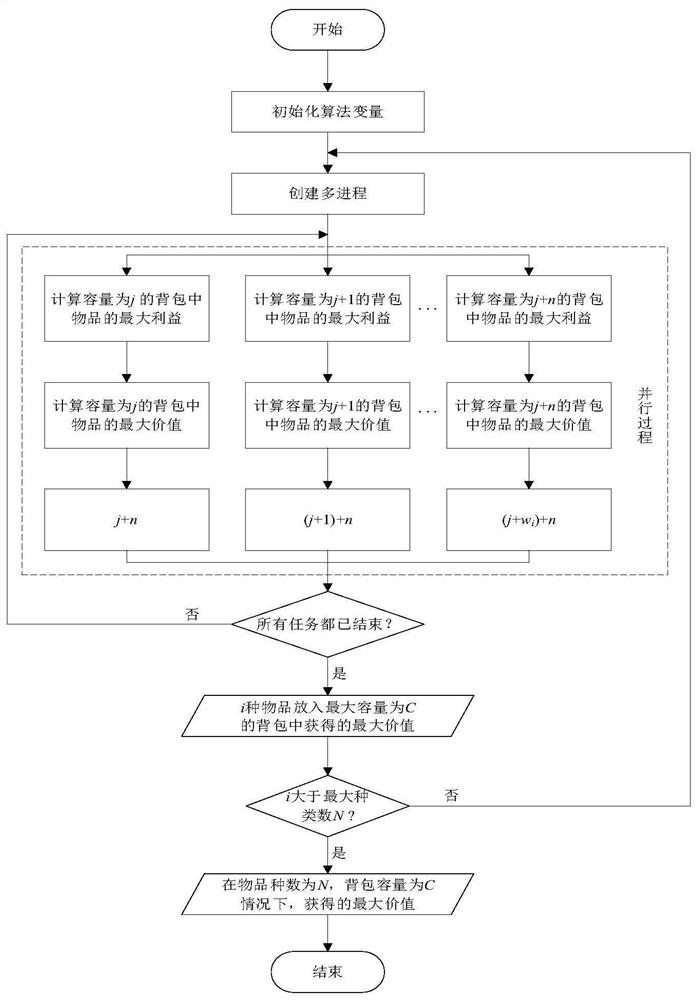
[0067] In this embodiment, on the basis of grouping the capacity state j in embodiment 1, the calculation tasks of multiple groups are executed in parallel. First, the maximum number of item types is defined as N in embodiment 1, the maximum capacity of the backpack is C, and the item type is i, 0≤i≤N, the individual value of each item is v i , with weight w i , the number of each item is k i ;Define a (N+1)×(C+1) two-dimensional value table f, the knapsack capacity is j, 0≤j≤C; f i (j) indicates the maximum value of putting i items into the knapsack when the capacity is j. When i=0 or j=0, the maximum value obtained is f (i＝0) (j) and f (j＝0) (i) are all 0.

[0068] Specifically, such as figure 2 As shown, the method of the present embodiment (hereinafter referred to as FBKP parallel) comprises the steps:

[0069] S1. Calculate the remainder a=j mod w i, there are n types of remainder a, group the capacity state j according to the capacity remainder a, put the capacit...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to the technical field of knapsack problem solving, and discloses a method for solving a bounded knapsack problem based on an improved dynamic programming algorithm, and the method comprises the steps of defining the maximum number of article types as N, the maximum capacity of a knapsack as C, the article types as i, i being greater than or equal to 0 and less than or equalto N, the single value of each article as vi, the weight as wi, and the number of each article is ki; defining an (N + 1) * (C + 1) two-dimensional value table f, the knapsack capacity is j, and j islarger than or equal to 0 and smaller than or equal to C; and calculating a remainder a, grouping the capacity states j according to the capacity remainder a, and calculating the capacity states j with the same capacity remainder in one group. According to the invention, the capacity states j are grouped according to the remainder, a traditional dynamic programming recursion formula is improved, redundant calculation brought by the BKP solving process is reduced, meanwhile, parallelization is conducted on the improved algorithm, and compared with an existing algorithm, the method has higher efficiency and can achieve rapid solving of the BKP along with increase of the data volume.

Description

technical field [0001] The invention relates to the technical field of knapsack problem solving, in particular to a method for solving a bounded knapsack problem based on an improved dynamic programming algorithm. Background technique [0002] The knapsack problem (KP) is a classic combinatorial optimization problem that is proven to be NP-hard. It has various practical applications in cryptography, decision optimization, task scheduling, cost control, and cargo loading. KP has several subproblems, such as 0-1 knapsack problem (0-1KP), bounded knapsack problem (BKP) and unbounded knapsack problem (UKP), etc. [0003] For the solution method of BKP, BKP is usually converted into an equivalent 0-1KP with multiple effective solutions for solution, which is the core concept of traditional dynamic programming (DP) algorithm to solve BKP (basic method). In other words, each item type i in BKP will generate k i independent copies. Due to k in 0-1KP i Item types are converted f...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/10G06Q10/04G06Q10/06
CPCG06F17/10G06Q10/04G06Q10/06
Inventor 万烂军张根龚坤李泓洋
Owner HUNAN UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com