Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Processing method, terminal, base station for feedback information

A technology of feedback information and processing methods, applied in communication between multiple stations, digital transmission system, error prevention, etc., can solve problems such as detection errors, repeated data transmission, system performance impact, etc., to achieve accurate reception and improve accuracy The effect of avoiding repeated sending

Inactive Publication Date: 2009-07-08
ZTE CORP
View PDF3 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In addition, since the PUCCH channel for sending ACK / NACK adopts a fixed modulation method, when the signal-to-noise ratio of the PUCCH channel is high, the system cannot use high-order modulation for the PUCCH information to improve the system capacity; when the signal-to-noise ratio of the PUCCH channel When it is relatively low, if the system detects the ACK / NACK message incorrectly, it will have a great impact on the system performance. That is, if the terminal sends an ACK message, but after passing through the channel, the base station detects it as a NACK message, which will cause data error. Necessary repeated transmission, if the terminal sends a NACK message, but after passing through the channel, the base station detects it as ACK information, which will cause the UE to not receive correct data
[0007] Due to the unbalanced channel conditions of each uplink component carrier, the base station will make an error in the detection of the ACK / NACK message carried by the PUCCH, which will reduce the transmission quality of the PUCCH channel, resulting in repeated data transmission or the terminal cannot receive correct data.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Processing method, terminal, base station for feedback information
  • Processing method, terminal, base station for feedback information
  • Processing method, terminal, base station for feedback information

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

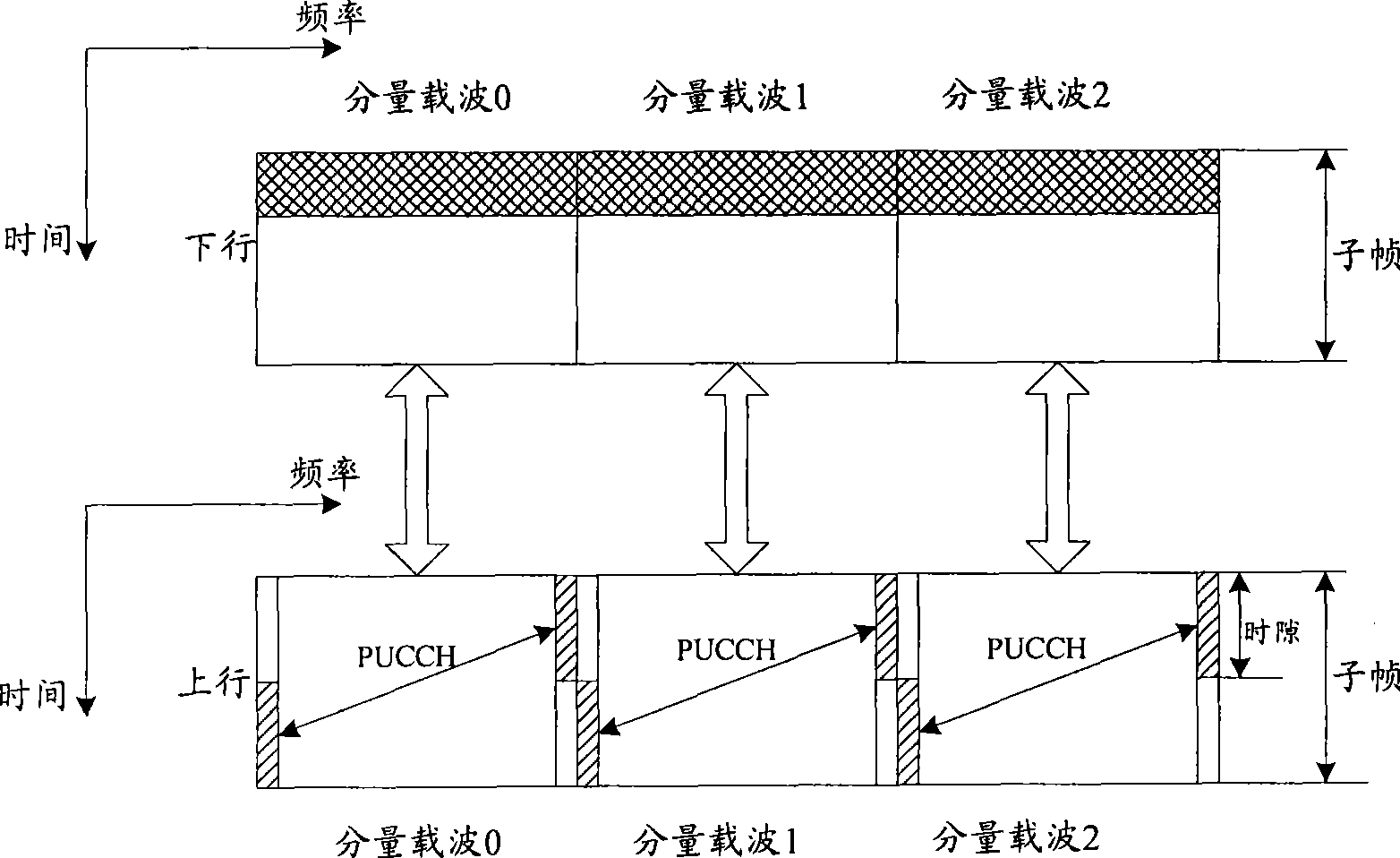
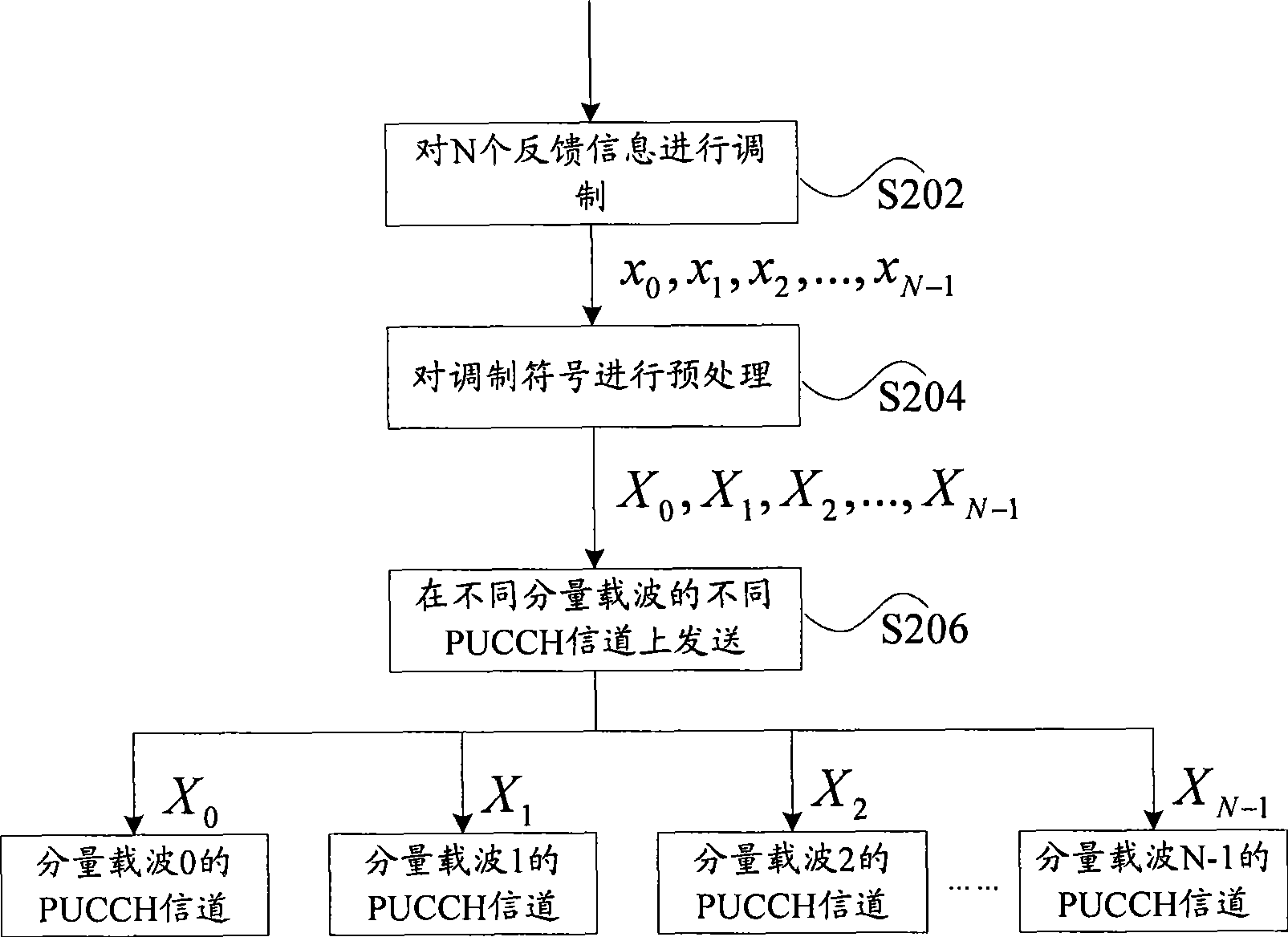
[0040] According to an embodiment of the present invention, a feedback information processing method is provided, which is used for a terminal to process a plurality of feedback information returned to a base station, wherein one piece of feedback information corresponds to one source modulation symbol, and the method includes: The source modulation symbols are preprocessed to obtain multiple target modulation symbols, where each target modulation symbol is correlated with multiple source modulation symbols. Wherein, the above preprocessing may be orthogonal processing or pseudo-orthogonal processing.

[0041] In the specific implementation process, the source modulation symbols can be preprocessed by the following formula to obtain multiple target modulation symbols: (X 0 , X 1 ,…X N-1 ) T =M(x 0 , x 1 ,...x N-1 ) T , where M is the transformation matrix, x 0 , x 1 ,...x N-1 Modulate symbols for multiple sources, X 0 , X 1 ,…X N-1 for x 0 , x 1 ,...x N-1 Corre...

Embodiment 1

[0052] The preprocessing of this example uses Fourier transform, and the transformation matrix is ​​a Fourier matrix, where the Fourier transform matrix is:

[0053] T = 1 1 1 · · · 1 1 e - j 2 π N 1 × 1 e ...

Embodiment 2

[0057] The preprocessing of this example adopts Walsh transformation, and the transformation matrix is ​​a Walsh matrix. This embodiment is applicable to the number N of feedback messages being 2, 4, 8, ..., that is, 2 n In the case of , for example, for the case of N=4, a 4th-order Walsh transform can be used. At this time, the Walsh transform matrix is:

[0058] T = 1 1 1 1 1 - 1 1 - 1 1 1 - 1 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a feedback message processing method, a terminal and a base station. The feedback message processing method is applied to a terminal for processing a plurality of feedback messages that are returned from the terminal to the base station, wherein one feedback message is in correspondence to one primary modulation symbol. The feedback message processing method comprises: a plurality of primary modulation symbols are pre-processed to obtain a plurality of target modulation symbols, wherein each target modulation symbol is related to the primary modulation symbols. The feedback message processing method improves the accuracy in detecting the acknowledgment / negative acknowledgment (ACK / NACK) messages carried by the physical unlink control channel (UCCH), improves the transmission quality of the PUCCH, avoids the repetitive data transmission, and ensures that the terminal can accurately receive the data.

Description

technical field [0001] The present invention relates to the communication field, in particular, to a method for processing feedback information, a terminal, and a base station. Background technique [0002] In the International Mobile Telecommunications-Advanced (IMT-Advanced for short) system, high-speed data transmission can be realized and the system capacity is large. In the case of low-speed mobile and hotspot coverage, the IMT-Advanced system The peak rate can reach 1Gbit / s. In the case of high-speed mobile and wide area coverage, the peak rate of the IMT-Advanced system can reach 100Mbit / s. [0003] In order to meet the requirements of the International Telecommunication Union-Advanced (ITU-Advanced for short), Long Term Evolution Advanced (LTE-Advanced for short), which is an evolution standard of the Long Term Evolution (LTE for short), Advanced) system needs to support larger system bandwidth (up to 100MHz), and needs to be backward compatible with existing LTE st...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L1/00H04B7/26
Inventor 夏树强梁春丽米德忠
Owner ZTE CORP
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com