Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Implementation algorithm for truncating one dimensional Debye medium Crank-Nicolson perfectly matched layer

A fully matching layer and algorithm technology, applied in computing, special data processing applications, instruments, etc., can solve problems such as low algorithm calculation accuracy, large algorithm error, and increased numerical dispersion

Inactive Publication Date: 2015-03-11
TIANJIN POLYTECHNIC UNIV
View PDF0 Cites 14 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] For the ADI-FDTD algorithm and the LOD-FDTD algorithm, although the stability conditions have been overcome to a certain extent, the calculation accuracy of the algorithm is too low and the performance is not ideal. The reason is that when the time step increases, the The numerical dispersion increases, which leads to a larger error in the algorithm

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Implementation algorithm for truncating one dimensional Debye medium Crank-Nicolson perfectly matched layer
  • Implementation algorithm for truncating one dimensional Debye medium Crank-Nicolson perfectly matched layer
  • Implementation algorithm for truncating one dimensional Debye medium Crank-Nicolson perfectly matched layer

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

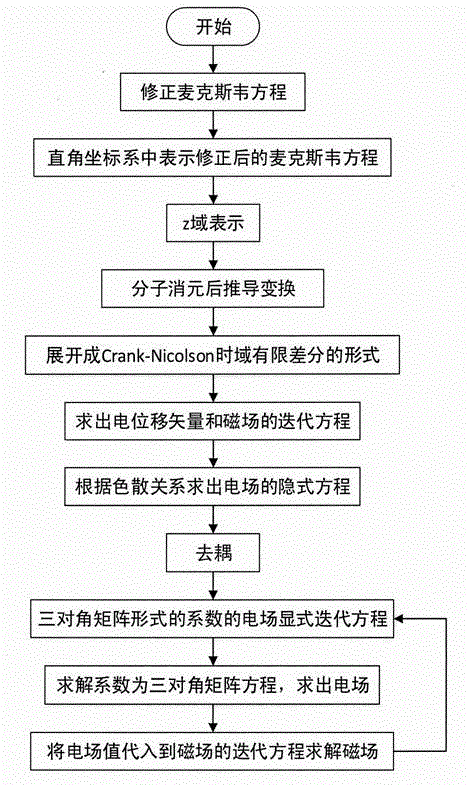
[0049] In order to make the object, technical solution and advantages of the present invention clearer, the implementation manner of the present invention will be further described in detail below in conjunction with the accompanying drawings.

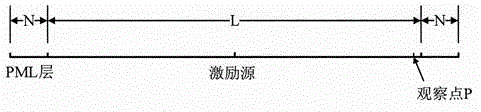
[0050] Step 1: If figure 1 , write the program in FORTRAN language according to the algorithm flow chart, and give specific calculation examples in the program, set the electromagnetic parameters of the computational space model, including the calculation area size: L+2×N, where L is the length of the calculation area ( unit: cell), N is the thickness of the perfectly matched layer (unit: cell); space step Δx; time step in is the maximum time step of traditional FDTD satisfying the numerical stability condition of CFL, and CFLN is the multiple of the time step of CN-FDTD relative to the time step of traditional FDTD; set the medium parameters of Debye medium.

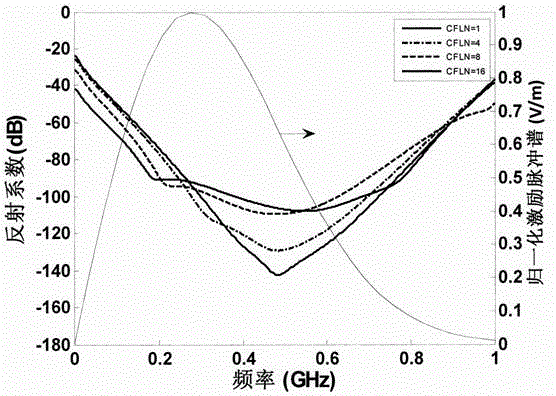
[0051] Step 2: If figure 2 , set the location and type of the excitatio...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an implementation algorithm for truncating a one dimensional Debye medium Crank-Nicolson perfectly matched layer, belongs to the technical field of numerical simulation, and aims to truncate a Debye dispersive medium by using the perfectly matched layer and simulate a limited memory space of a computer into an infinite space to simulate the propagation characteristic of electromagnetic wave in the Debye dispersive medium. The algorithm is characterized by comprising the following steps: a plurality of stretch coordinate variables are converted from a frequency domain to a z domain by using a bilinear transformation method, then a maxwell equation is dispersed in the time domain by using a Crank-Nicolson finite difference time domain method, an explicit iterative equation of an electric field is induced, and finally a value of an electromagnetic field component is solved. The algorithm has the advantages of unconditional stability and capabilities of improving the electromagnetic field calculation speed and saving memory.

Description

technical field [0001] The invention relates to the technical field of numerical simulation, in particular to a truncated one-dimensional Debye medium Crank-Nicolson complete matching layer realization algorithm. Background technique [0002] The finite difference time domain method (FDTD) is a direct time domain method for solving Maxwell's differential equations, and it is one of the most widely used calculation methods in the electromagnetic field numerical calculation methods. [0003] However, with the deepening of scientific research and the needs of more and more widely used applications, the defect that the algorithm itself is limited by the Courant Friedrichs Lewy (CFL) numerical stability conditions has become more and more prominent. In practical applications, all The selected time step is very short, which means that when solving the electromagnetic field problem numerically, the calculation time will increase rapidly and errors will accumulate. In order to over...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
Inventor 李建雄于洋史伟光
Owner TIANJIN POLYTECHNIC UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com