Method for solving node impedance matrix of electric system on basis of Gaussian elimination method of sparse symmetric matrix technology
A technology of node impedance matrix and Gaussian elimination method, which is applied in the field of power system analysis and calculation, can solve the problems of simplification of calculation process or improvement of calculation speed without advantages, slow calculation speed, unfavorable data processing in symmetrical matrix, etc. Substituting calculation speed, reducing the amount of calculation, and reducing the effect of invalid calculation of elements
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
[0047] A comparison of the calculation process without considering the sparsity of elements, considering the sparsity of elements, and considering the symmetric sparsity of elements. After performing elimination with normalization, the Y array becomes the following Y (n-1) 'Array.
[0048]
[0049] Suppose Y 31 ≠0, then for Y 31 Element to be eliminated. Definition: Y 11 The elements are diagonal elements; Y 11 All elements on the right side of Y 1j are cross elements; Y 31 The element is an elimination element; Y 31 All elements on the right side of Y 3j is the computational element.
[0050] (1) Regardless of the sparsity of elements, Y must be calculated 31 All computed elements to the right of the element Y 32 , Y 33 ,….
[0051] (2) Considering the sparsity of elements, only calculate Y 31 The crossing Y of the row to the right of the element and non-zero 1j All calculated elements Y that interact with the column the element is in 3j (1
Embodiment 2
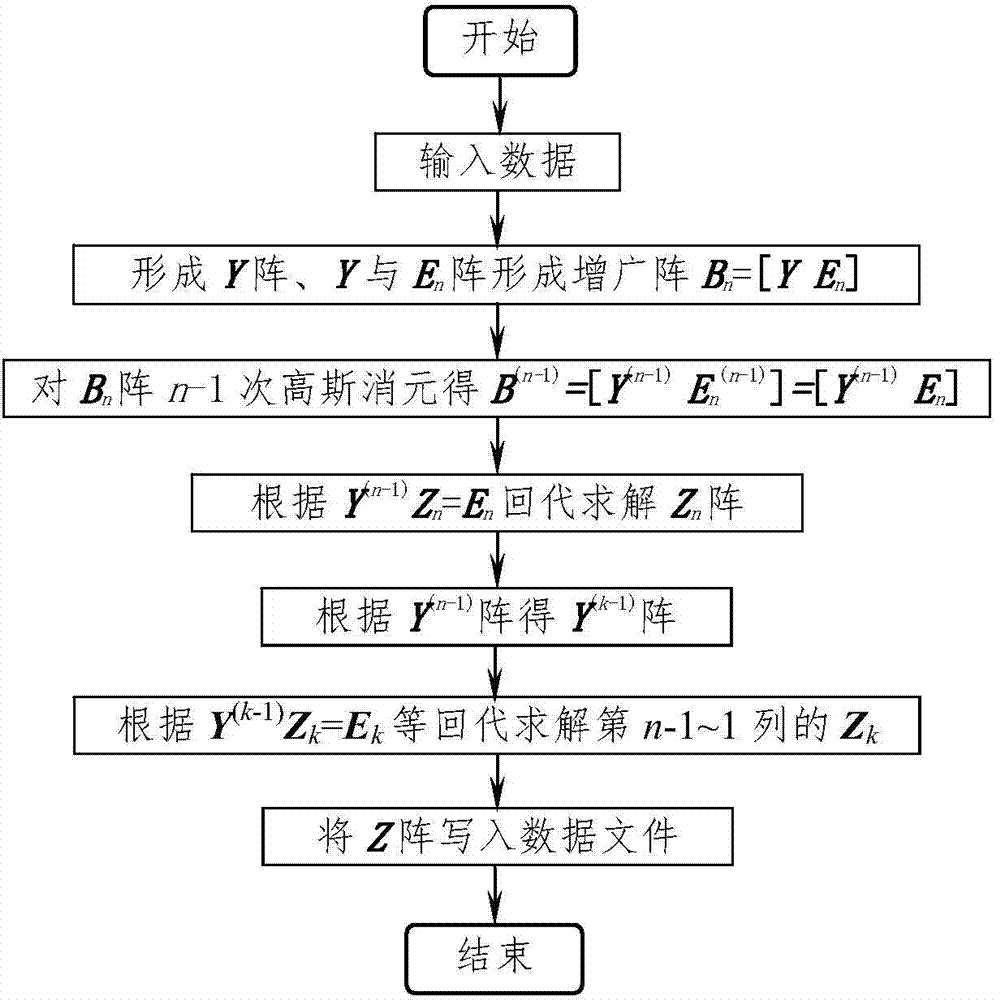
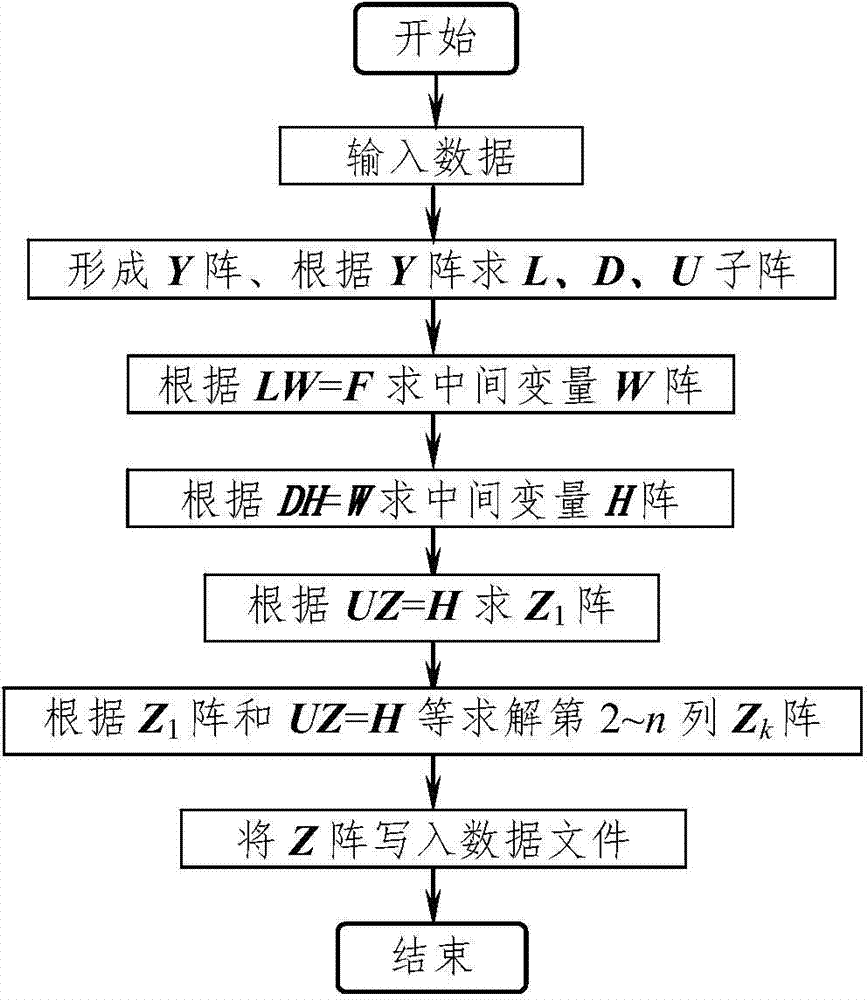
[0054] Using the traditional unnormalized Gaussian elimination method ( figure 1 ), LDU triangular decomposition method ( figure 2 ) and the inventive method ( image 3 ) Find the elements of the Z matrix for the Y matrix of the IEEE-30, -57, -118 node systems, and compare the average calculation time. The calculation results are shown in Table 1.
[0055] Table 1 Gaussian elimination method without normalization, LDU triangular decomposition method and the comparison of the present invention's Z matrix calculation time
[0056]
[0057] T 1 : Average calculation time of Gaussian elimination method without normalization;
[0058] T 2 : Average calculation time of LDU triangular decomposition method;
[0059] T 3 : the average calculation time of the inventive method;
[0060] T 2 / T 1 : The average calculation time percentage of LDU triangular decomposition method and unnormalized Gaussian elimination method;
[0061] T 3 / T 1 : the average calculation time pe...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com