Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Optimal transportation meshless method for solving large deformation of material

A large deformation, meshless technology, applied in design optimization/simulation, special data processing applications, instruments, etc., can solve problems such as tensile stress instability, to solve tensile stress instability, overcome high computing costs, The effect of improving computational efficiency

Active Publication Date: 2017-02-22
云翼超算(北京)软件科技有限公司
View PDF2 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At the same time, its optimal transport time integration scheme ensures the mass and momentum conservation and symplectic conservation of the system under time discretization. Since the interpolation and integration are performed at different discrete points, the problem of tensile stress instability is solved.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimal transportation meshless method for solving large deformation of material
  • Optimal transportation meshless method for solving large deformation of material
  • Optimal transportation meshless method for solving large deformation of material

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

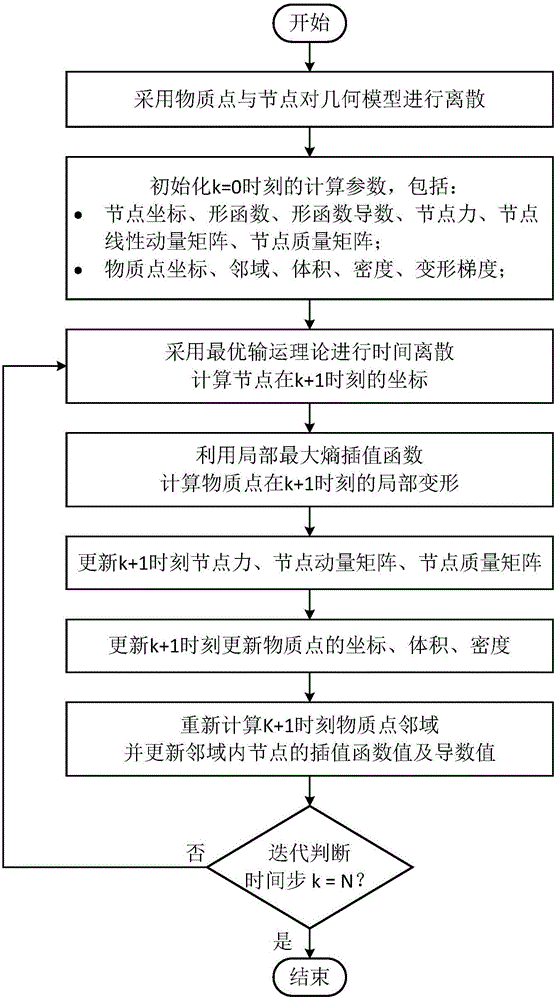
[0031] In the following, the technical solution of a gridless method for optimal transportation of large deformation of materials in the present invention will be further described in conjunction with the accompanying drawings.

[0032] like figure 1 Shown, the present invention is concretely realized as follows:

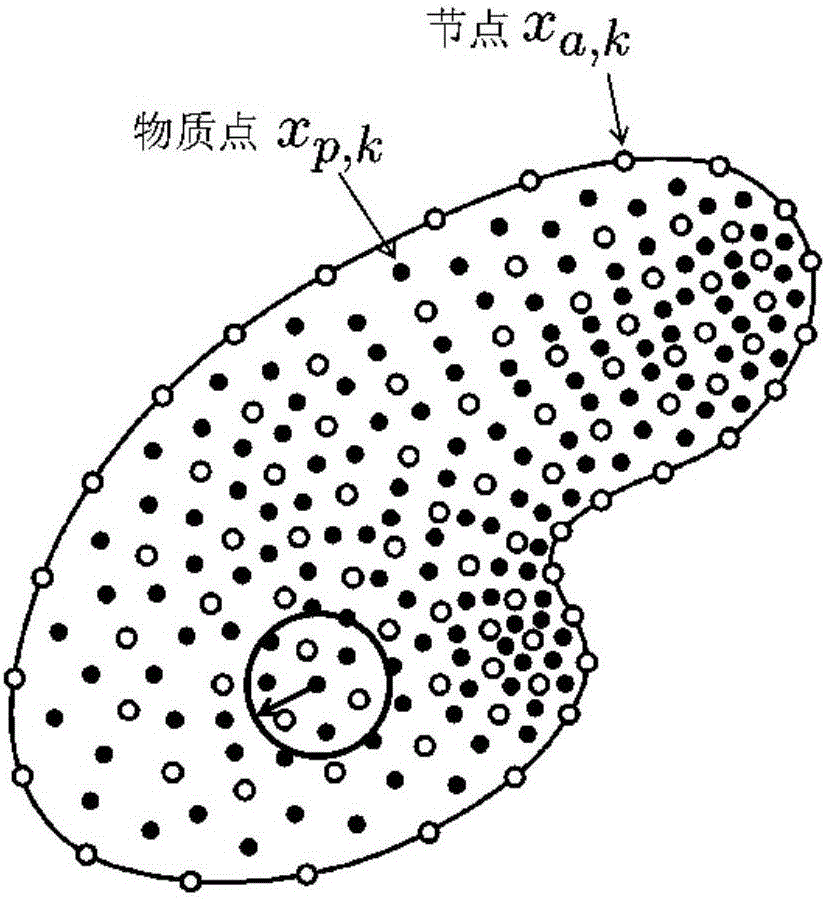
[0033] (1) The geometric model is discrete. The present invention is applicable to various material models. Which material to use in the specific calculation process needs to be determined according to the actual situation of the user. When performing material dynamic response analysis (such as figure 2 metal target plate impact test shown), let Ω represent the d-dimensional continuum problem domain (ie, the geometric model) and discretize the geometric model Ω into a set of material point sets {x p,k ,p=1,2,…,m; k=0,1,…,N} and a set of node sets {x a,k , a=1,2,...,n; k=0,1,...,N}. like image 3 As shown, the hollow dots represent nodes: x a,k (a is the node i...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an optimal transportation meshless (OTM) method for solving large deformation of a material and aims at solving the problems of effective and stable solving of maximum deformation, high-speed impact and geometric distortion, metal material molding, multiphase coupling and the like. The OTM method adopts a material point and node pair original problem domain to perform discretion and adopts a local maximum entropy interpolation function to construct a continuous movement function, and the problem that mesh distortion caused in maximum deformation processed by adopting a finite element method, the problem that a Dirichlet boundary condition cannot be directly added for a meshless method, calculating misconvergence and the like are avoided. In addition, due to the fact that interpolation and integration are performed at different discrete points, an effective meshless numerical integration mode is provided, and the problem of tensile stress instability is solved. The OTM method serves as an incremental updating Lagrangian method to make mass conservation automatically achieved without solving. Time discretion is performed by adopting an optimal transportation theory, the momentum conservation and symplectic conservation of a discrete system are ensured, and the operation efficiency and precision are greatly improved.

Description

technical field [0001] The invention relates to a method for solving the dynamic response of materials in the problem of continuum mechanics, in particular to a meshless method for solving the dynamic response of materials in the problem of continuum mechanics, which belongs to the technical field of computational mechanics and numerical simulation, and is mainly used for solving Extremely large deformation, dynamic crack growth, high-speed impact and geometric distortion, material fission, metal material forming and multi-phase transformation, etc. Background technique [0002] The finite element method is used to deal with complex physical phenomena in modern engineering systems, including: extremely large deformation problems; dynamic crack growth problems; high-speed impact and geometric distortion problems; material fission problems; metal material forming problems and multi-phase transformation problems, etc. When the finite element solution is difficult or even fails ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
CPCG06F30/20
Inventor 黎波
Owner 云翼超算(北京)软件科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com