Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Analytical Astronomical Positioning Method Projected to Equinox Equatorial Coordinate System

A technology of astronomical positioning and vernal equinox, which is applied in astronomical navigation, navigation calculation tools, etc., can solve the problems of increasing the amount of calculation, etc., and achieve the effect of simple calculation and real-time calculation of astronomical positioning

Active Publication Date: 2019-09-03
李清林
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0012] For continuous observation of the same celestial body, because the position of the celestial body is changing all the time, each observation data solution needs to obtain the position of the celestial body according to the observation time. Analytical and real-time calculation of astronomical positioning is obviously an unfavorable factor that increases the amount of calculation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Analytical Astronomical Positioning Method Projected to Equinox Equatorial Coordinate System
  • Analytical Astronomical Positioning Method Projected to Equinox Equatorial Coordinate System
  • Analytical Astronomical Positioning Method Projected to Equinox Equatorial Coordinate System

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

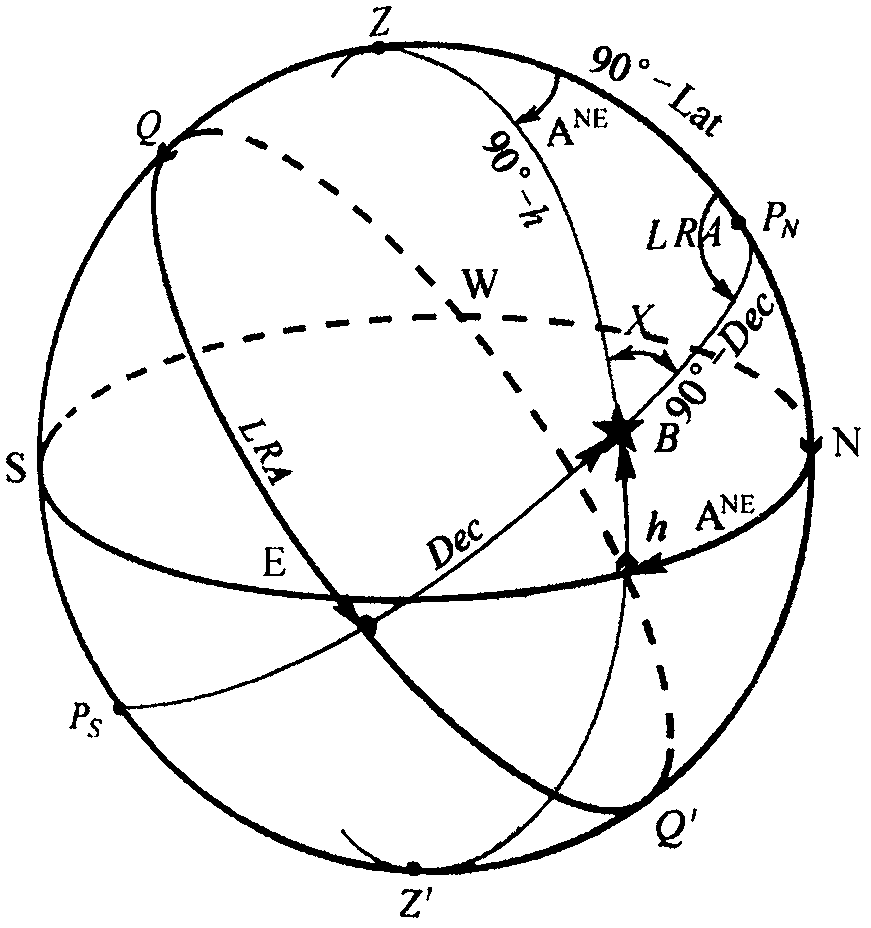
[0034] Specific embodiment 1, observe the true azimuth A and true height h of the unknown celestial body B at the known position Z (Lat / Long), and calculate the position of the celestial body; obtain the right ascension GRA of the Green point according to the time, and project the position Z of the observer to the vernal equinox Equatorial coordinate system In the astronomical triangle, such as figure 1 Shown: Given the three elements of top distance (90°-h), cosine latitude (90°-Lat) and azimuth A, use the cosine formula to solve the residual distance (90°-Dec):

[0035] cos(90°-Dec)=cos(90°-h)*cos(90°-Lat)

[0036] +sin(90°-h)*sin(90°-Lat)*cos(A)

[0037] =sin(h)*sin(Lat)+cos(h)*cos(Lat)*cos(A)

[0038] Solve the residual distance (90°-Dec), and get the declination Dec of the celestial body; then use the cosine formula to deform and solve the local right ascension LRA:

[0039]

[0040] Calculate the local right ascension LRA and get the celestial right ascension RA=LR...

specific Embodiment approach 2

[0041] Specific embodiment 2, observe the true azimuth A and the true altitude h of the known celestial body B (Dec / RA) at the unknown position Z, and calculate the position of the measurer; obtain the right ascension of the Green point GRA according to the time, and project the position Z of the measurer to The equinox equatorial coordinate system, in the astronomical triangle, such as figure 1 Shown: Knowing the three elements of residual distance (90°-Dec), top distance (90°-h) and azimuth A, use the sine formula to solve the local right ascension LRA:

[0042]

[0043] Solve the local right ascension LRA, get the longitude Long=RA-LRA-GRA; then use Napier's formula deformation to solve the co-latitude (90°-Lat):

[0044]

[0045] The co-latitude (90°-Lat) is obtained through the calculation, and the latitude Lat is obtained; the position (Lat, Long) of the tester is obtained.

specific Embodiment approach 3

[0046] Specific embodiment 3, observe a known celestial body B (Dec / RA) at a known position Z (Lat / Long), and calculate the true azimuth A and true height h of the celestial body; obtain the right ascension GRA of the Green point according to the time, and measure the position Z projection to equinox equatorial coordinate system From the celestial right ascension RA and the observer's right ascension RA Z Get local right ascension LRA=RA-RA Z , in the astronomical triangle, such as figure 1 Shown: Given the three elements of margin (90°-Dec), co-latitude (90°-Lat) and local right ascension LRA, use the cosine formula to solve the top distance (90°-h):

[0047] cos(90°-h)=cos(90°-Dec)*cos(90°-Lat)

[0048] +sin(90°-Dec)*sin(90°-Lat)*cos(LRA)

[0049] =sin(Dec)*sin(Lat)+cos(Dec)*cos(Lat)*cos(LRA)

[0050] Solve the top distance (90°-h) and get the height h; then use the cosine formula to deform and solve the azimuth A:

[0051]

[0052] The azimuth A is obtained throug...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a celestial positioning analysis method achieved by projecting a subject position to a spring equinox equatorial coordinate system. The celestial positioning analysis method achieved by projecting the subject position to the spring equinox equatorial coordinate system comprises the steps that the subject position is projected to the spring equinox equatorial coordinate system; a celestial triangle is established in the spring equinox equatorial coordinate system; celestial body position or subject position data is obtained by utilizing observed celestial body azimuth or height data and solving the celestial triangle and a correlated spherical triangle. Compared with the prior art, the method has the advantages that analytical celestial positioning calculation is easy and convenient, and particularly, calculation is easier and more convenient by observing the same celestial body multiple times; observation of the azimuth or height of two celestial bodies and determination of the celestial body position do not strictly require simultaneousness and can be conducted in a period of time; achievement of continuous tracking and real-time celestial positioning solving is promoted; almanacs such as a nautical almanac giving a celestial body Greenwich hour angle can be significantly simplified; a novel celestial positioning method is provided for determining the celestial body position or subject position.

Description

technical field [0001] The invention relates to a method for determining the position of a celestial body or a measurer, in particular to an analytic astronomical positioning method projected to the equatorial coordinate system of the vernal equinox. Background technique [0002] The principle of astronomical positioning is to obtain the projection point of the celestial body on the ground according to the observation time, obtain the center of the astronomical position circle, correct the height of the observed celestial body to the true height to obtain the true top distance, obtain the radius of the astronomical position circle, and obtain two astronomical position circles by observing two celestial bodies. Position circle, there are generally two points where two astronomical position circles intersect, and the point close to the estimated position is the observation position; [0003] The principle of the altitude difference method is to select the position of the ship ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01C21/02G01C21/20
Inventor 李清林
Owner 李清林
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com