Transformer fault classification and identification method based on vibration analysis method

A technology for transformer faults and identification methods, which is applied to instruments, measuring electrical variables, measuring devices, etc., and can solve problems such as inability to achieve nonlinear classification, adverse observation, and influence.

Active Publication Date: 2017-05-10
GUANGAN POWER SUPPLY COMPANY STATE GRID SICHUANELECTRIC POWER +1
View PDF7 Cites 31 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, according to EEMD, the feature vector of the transformer vibration signal is extracted, the feature vector is multiple sets of data, and when there are many test samples, the test sample will become a multidimensional array
Multidimensional arrays are not conducive to calculations, and are not conducive to observation in reality; at the same time, Fisher's discriminant method can only achieve linear classification, but cannot achieve nonlinear classification. In the experimental data, due to the uncertainty of the experimental measurement data, it is inevitable that there will be wrong data. These erroneous data will affect the effect of linear classification

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Transformer fault classification and identification method based on vibration analysis method
  • Transformer fault classification and identification method based on vibration analysis method
  • Transformer fault classification and identification method based on vibration analysis method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

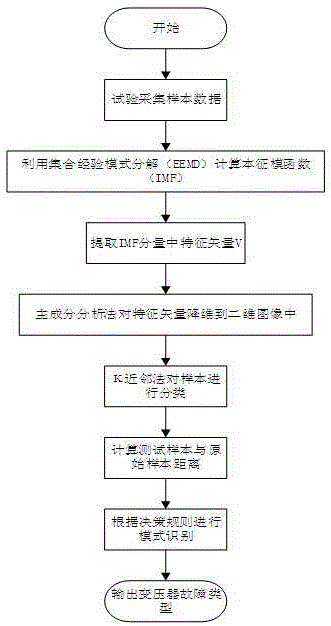
[0060] Such as figure 1 The shown transformer fault classification and identification method based on the vibration analysis method includes the following steps:

[0061] S1: Select the corresponding transformer as the test object, and collect the vibration signals of the transformer in different states as sample data;

[0062] S2: Using the set empirical mode decomposition method in the Hilbert-Huang transform to calculate the sample data to obtain the eigenmode function;

[0063] S3: extracting the characteristic vector V in the intrinsic modulus function component;

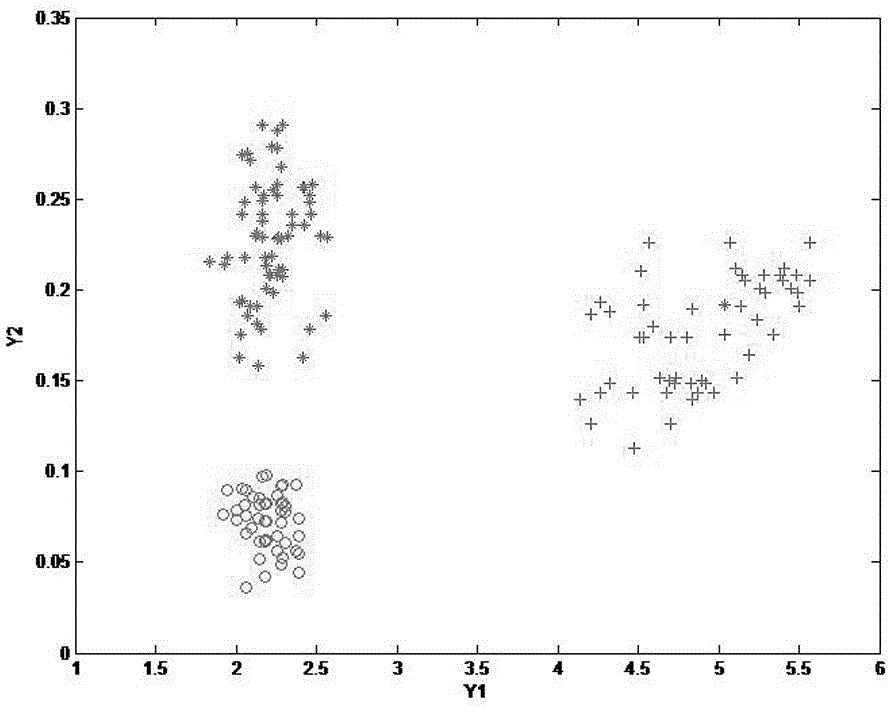
[0064] S4: Use the principal component analysis method to reduce the dimensionality of the feature vector, and project the coordinates into the two-dimensional image;

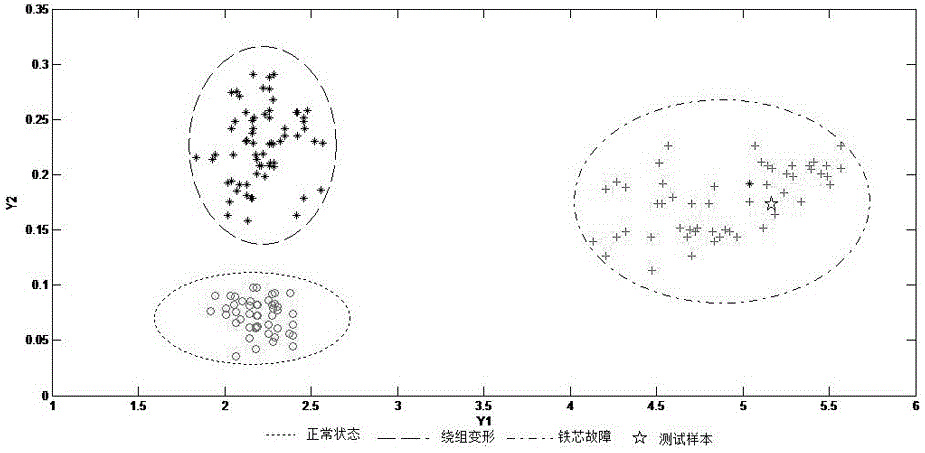
[0065] S5: Classify the sample data using the K-nearest method;

[0066] S6: Using the distance formula to calculate the distance between the test sample and the original sample;

[0067] S7: performing pattern recognition;

[0068] S8: Out...

Embodiment 2

[0070] On the basis of the foregoing examples, specifically:

[0071] In step S2, the steps of calculating the sample data to obtain the intrinsic modulus function by using the set empirical mode decomposition method in the Hilbert-Huang transform are as follows:

[0072] Add M times of Gaussian white noise sequence n to the original signal x(t) i (t), (i=1, 2, ..., M), namely:

[0073] ;

[0074] to x i (t) Carry out EMD respectively to obtain the components and margins of each eigenmode function, namely:

[0075] ;

[0076] where h ij After adding Gaussian white noise for the ith time, for X i (t) the jth eigenmode function component obtained by decomposing; r in After adding Gaussian white noise for the ith time, for X i (t) remainder after decomposing; n is the number of decomposition levels;

[0077] Using the zero-mean principle of the Gaussian white noise spectrum, the eigenmode function components corresponding to the above steps are generally averaged to ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a transformer fault classification and identification method based on a vibration analysis method. The method comprises the following steps: S1) selecting a transformer test object, and collecting transformer vibration signals under different states as sample data; S2) calculating the sample data by utilizing a Hilbert-Huang transform EEMD (ensemble empirical mode decomposition) method to obtain an intrinsic mode function; S3) extracting characteristic vector V in each intrinsic mode function component; S4) carrying out dimensionality reduction on the characteristic vector through a principal component analysis method, coordinates being projected to a two-dimensional image; S5) carrying out classification on the sample data through a K neighbor method; S6) calculating the distance between a test sample and an original sample through a distance formula; S7) carrying out mode recognition; and S8) outputting corresponding transformer fault type in mode recognition. Operation state of a transformer can be judged visually and effectively.

Description

technical field [0001] The invention relates to the field of electric equipment detection, in particular to a transformer fault classification and identification method based on a vibration analysis method. Background technique [0002] Among the various equipment in the power system, the transformer is an expensive and important equipment, and its reliability is of great significance to ensure the safe operation of the power grid. The fault statistics of transformers over the years show that transformer windings and iron cores are the most faulty components, and transformer accidents caused by windings and iron cores account for 70% of the total transformer accidents. [0003] At present, there are more and more methods for detecting the operation status of transformers. The short-circuit impedance method judges the winding deformation by measuring the reactance of the winding off-line and observing the change of its impedance value, but this method has low sensitivity and...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
Patent Type & Authority Applications(China)
IPC IPC(8): G01R31/06G01H17/00
CPCG01H17/00G01R31/72
Inventor 李敏陈果石同春沈大千秦少鹏向天堂邓权伦罗宇昆高翔陈大浩
Owner GUANGAN POWER SUPPLY COMPANY STATE GRID SICHUANELECTRIC POWER
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap