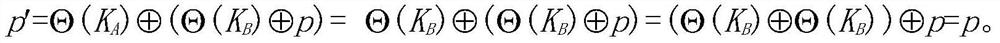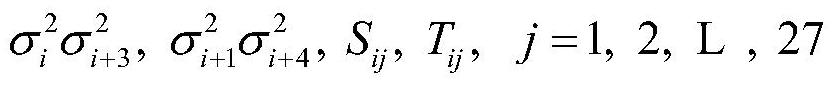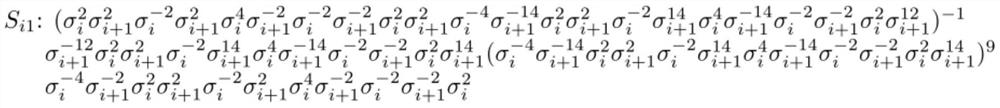Method for establishing secure public-key cryptography against quantum computing attacks
A technology of public key cryptography and quantum computing, which is applied in the fields of public key encryption technology, identity authentication technology, and digital signature technology, and can solve problems such as hidden dangers of public key cryptography.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0044] A public key cryptographic protocol against quantum computing attacks of the present invention will be further described in detail below in conjunction with embodiments.
[0045] 1. Establish a platform for public key cryptographic protocols
[0046] The platform for establishing all public-key cryptographic protocols is an infinite non-abelian group G and two subgroups A and B of G, so that for any a∈A and any b∈B, the equation ab=ba holds. In addition, due to the needs of encoding and key generation, G must also meet the following conditions:
[0047] 1) Words representing elements of G on the generator set of G have a computable normal form;
[0048] 2) G is at least exponential growth (exponential growth), that is, the number of elements in G whose word length is a positive integer n is bounded by an exponential function about n;
[0049] 3) The product operation and inversion operation based on the normal form of the group are feasible and computable.
[0050] F...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com