Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Arbitrary power square root solving method for single-precision floating-point number and solver of arbitrary power square root solving method

A floating-point, single-precision technology, used in instruments, electrical digital data processing, digital data processing components, etc., can solve problems such as unfavorable hardware implementation and increased computing resources, and achieve fast computing speed, high computing frequency, and expansion. Application-wide effects

Active Publication Date: 2020-04-28
NANJING UNIV
View PDF3 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Newton iteration method and digital recursion method need to use a large number of multipliers and adders, and when calculating high-order square roots, computing resources will increase sharply, which is not conducive to hardware implementation
The method based on CORDIC can only realize the calculation of any power root of fixed-point numbers at present, which has certain limitations.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Arbitrary power square root solving method for single-precision floating-point number and solver of arbitrary power square root solving method
  • Arbitrary power square root solving method for single-precision floating-point number and solver of arbitrary power square root solving method
  • Arbitrary power square root solving method for single-precision floating-point number and solver of arbitrary power square root solving method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

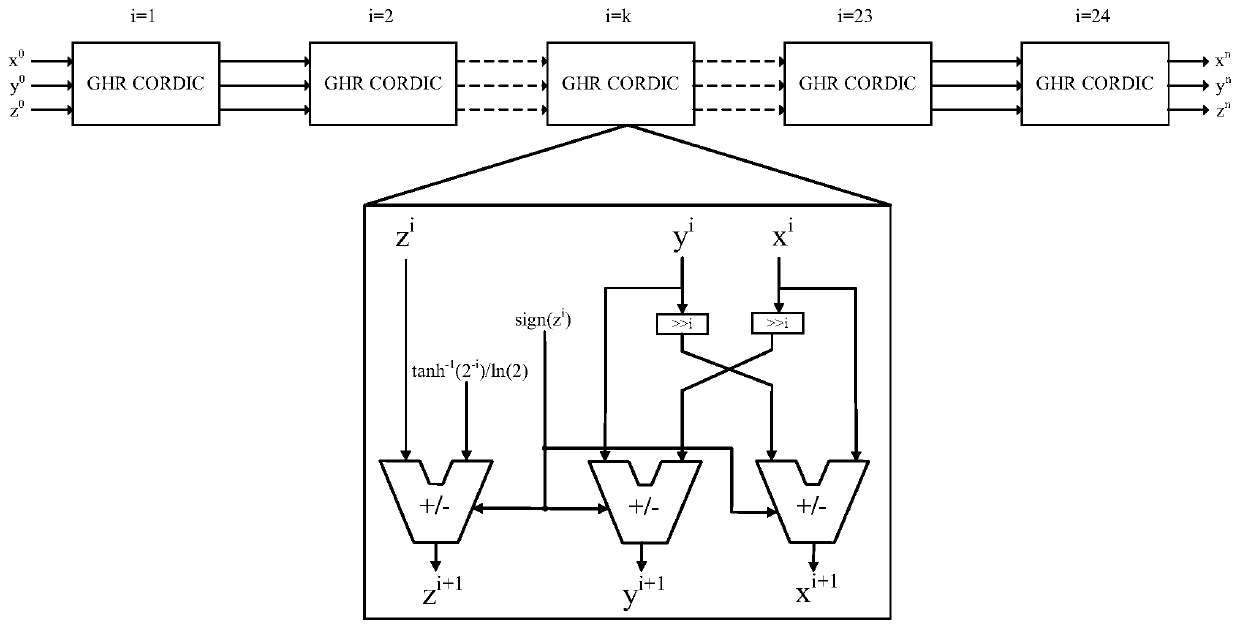
[0067] (1) In the present embodiment, the number of iterations of the generalized hyperbolic CORDIC algorithm in the arctangent calculation module (GHVCORDIC) of the generalized hyperbolic CORDIC and the sine and cosine calculation module (GHRCORDIC) based on the generalized hyperbolic CORDIC is set to 24. At the same time, in order to match the pipeline, the number of iterations of the CORDIC algorithm in the CORDIC-based division calculation module (LVCORDIC) is also set to 24. Based on the hardware circuit of the above-mentioned setting design embodiment, taking the sine and cosine calculation modules of the generalized hyperbolic CORDIC as an example, its pipeline hardware architecture is as follows image 3 shown. For the designed hardware circuit, the calculation accuracy and hardware resource consumption are analyzed.

[0068] Set the data bit width of each calculation module according to the calculation iteration of the above settings, as shown in the following table:...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an arbitrary power square root solving method for a single-precision floating-point number and a solver of the arbitrary power square root solving method. The solver comprises:a division calculation module for carrying out division operation on an input power root value N; an arc tangent value calculation module for carrying out arc tangent value calculation operation on amantissa part M of the input single-precision floating-point number and obtaining a log2M; a calculation module for carrying out multiplication and addition operation on an exponent part E of a single-precision floating-point number, a reciprocal 1 / N of the root value N of the power and the log2M of the numerical value; a sine and cosine calculation module for solving hyperbolic sine and cosine values with 2 as the bottom for the calculation result obtained by the calculation module; and a calculation result integration module for summing the solved hyperbolic sine and hyperbolic cosine valuesand integrating the sum with an intermediate calculation result of the index part E to obtain a final calculation result in a single-precision floating-point number format. The solver provided by theinvention can calculate any power root value of any single-precision floating-point number, and has certain universality.

Description

technical field [0001] The invention relates to a method for solving an arbitrary power root of a single-precision floating-point number, and belongs to the technical field of digital signal processing. Background technique [0002] In today's microprocessor computing, nothing is more used than multipliers and adders. Therefore, relevant research is also spewing out. Whether it is from the improvement of the algorithm or the improvement of the hardware computing architecture, many scholars have made contributions, and related academic achievements are also emerging in endlessly. However, there are few optimization schemes for calculating the root of any power. [0003] Although the calculation of arbitrary power roots is not as common as the multiplication and addition operations in microprocessor computing, it also has a wide range of application scenarios. Taking quadratic root calculation as an example, it has important applications in spectrum analysis, audio signal pr...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F7/483G06F7/487G06F7/485
CPCG06F7/483G06F7/4876G06F7/485
Inventor 潘红兵王宇宣罗元勇
Owner NANJING UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com